不同发展演化方式下的电网统计特性和鲁棒性分析
冯 乾,马天琳,齐 程,朱红路,姚建曦,亢 楠,施辉伟,梁俊霞
(1.云南电网公司 北京能源新技术研究发展中心,北京100084;2.华北电力大学 新能源电力系统国家重点实验室,北京102206)
3 结 论
0 引 言
电网正发展成为世界上最复杂的人造网络之一,电网中的发电厂和变电站不仅数量众多,它们之间的连接也越来越复杂。近年来频发的大停电事故表明,复杂电力网络在满足用户用电需求的同时,局部故障或外界攻击诱发的大停电事故对电网乃至社会造成的影响也越来越严重[1,2]。因此,分析大停电事故发生机理并据此寻找积极防御策略和最优电网发展演化方式尤为必要。
研究表明,大停电事故大都是电力系统中单一元件或局部故障诱发连锁故障,致使系统中元件相继退出运行,最终导致大规模停电事故发生,甚至整个电网崩溃。梅生伟等将现有电力系统连锁故障模型分为以下三类:(1)基于复杂网络理论的连锁故障模型,主要包括Motter-Lai 模型、相隔中心性模型和有效性能模型;(2)基于元件级联失效的连锁故障模型,主要包括分支过程模型和CASCADE 模型;(3)基于电网动态特性描述的连锁故障模型,主要包括:OPA 模型、Manchester 模型和隐性故障模型[3]。其中,基于复杂网络理论的连锁故障模型从宏观的网络拓扑结构角度出发,模拟连锁故障传播过程,剖析大停电发生机理,建模简单,适用于节点数目巨大的复杂的电力系统连锁故障研究。近年来一大批研究者采用该方法构建了复杂网络模型[4~11]和连锁故障模型[12],分析了元件故障诱发的连锁故障对网络结构和性能的影 响[13~15],并 提 出 了 一 些 有 效 的 防 控 策略[16~20]。在复杂网络建模方面,比较经典的有ER 随机网络模型[4]、具有小世界特性的WS 网络模型[5]和NW 网络模型[6],以及具有无标度特性的BA 网络模型[7]。实证研究表明:部分电网具有小世界特性或无标度特性,因此许多研究者以上述经典模型为研究对象,开展了网络鲁棒性和防控措施研究。然而多数实际电网的结构与ER,WS,NW 和BA 网络存在一些差别,主要表现在度分布并非严格服从指数分布或幂律分布,最大节点度小于与之具有相同规模的无标度网络。因此,Liu[8]等考虑电网发展演化过程中存在一些不确定因素,在BA 网络模型[7]的基础上提出改进无标度网络发展模型,有效地降低了网络的最大节点度。Li[9]等在建模时首先随机选择一些节点作为新增节点的局域世界,然后再从局域世界中根据度优先原则择优选择新增节点的连接节点,得到的网络的度具有幂律特性、聚类系数较大而平均最短路径较小。此外,该模型也有效地降低了网络的最大节点度。曹一家[10]等同时考虑节点的度和空间距离对电网发展演化的影响,提出了时空演化发展模型。Mei[11]等综合能源和负荷分布、节点的电压等级和空间距离等对新增电厂和变电站的选址、定容和接入方式的影响,提出了小世界电网生长演化模型。
本文根据上述文献[8~11]提出的改进无标度发展模型、局域世界发展模型、小世界电网生长演化模型和时空演化模型,建立了与云南电网具有相容规模和相同连接数的改进无标度网络、局域世界网络、小世界电网和时空演化网络;并通过对比分析上述5 个网络的统计特性和对单一元件故障的耐受能力(鲁棒性),找出最优的电网发展演化方式,为电网规划和设计提供参考和依据。
1 复杂网络统计特性
在复杂网络理论中,通常将电网中的发电厂和变电站简化为网络中的节点,将连接发电厂和变电站之间的连接线路简化为边。据此,将云南电网简化为拥有88 个节点和110 条边的网络,并根据文献[8 ~11]建立了与云南电网具有相容规模(节点数相同)和相同连边数的改进无标度网络(Improved scale-free)、局域世界网络(Local world)、小世界电网(Small world)和时空演化网络(Space time)。假设初始网络拥有n0个节点,m0条边,各网络可通过重复如下步骤得到:
(1)改进无标度网络[8]:每次新增1 个节点,根据优先概率选择m 个已有节点与新增节点连接。在该模型中,节点i 的优先连接概率为
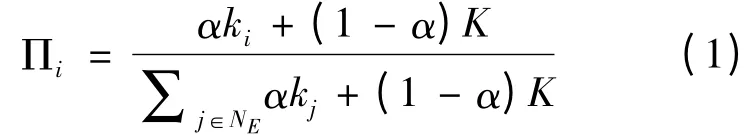
式中:α(0≤α≤1)是比例系数,表征节点度和不确定性因素所占的比例;ki是节点i 的度;NE表示网络中已有节点;K 为不确定性因子,该因子包括电网演化过程中的不确定因素。
(2)局域世界网络[9]:每次新增1 个节点,从已有节点中随机选取M 个节点作为新增节点的局域世界,根据优先连接概率选择局域世界中的m个节点与新增节点连接。节点i 优先连接概率为

式中:t 表示已经增加节点的次数;Local 表示局域世界中节点集合。
(3)时空演化网络[10]:每次新增1 个节点,其坐标从网络生长点(靠近网络中已有节点但尚未被占据的位置)中随机选择;根据优先连接概率选择m 个已有节点与新增节点连接。节点i 优先连接概率为
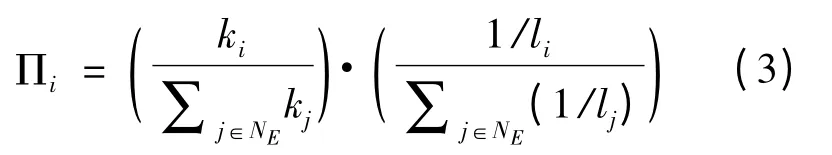
式中:li表示节点i 到新增节点的距离。
(4)小世界电网发展模型[11]:根据实际需求每次新增一定数量的发电厂节点和变电站节点,其坐标从网络节点中根据能源和负荷分布情况择优选择,并根据能源大小和负荷需求量确定新增节点的电压等级;根据网络中已有节点与新增节点之间的距离和电压等级择优选择节点与新增节点连接。表1 列出了这5 个网络的统计特性。

表1 复杂网络的统计特性Tab.1 Statistical characteristics of complex networks
显然,云南电网的特征路径长度、网络直径和平均介数都大于其余4 个网络,但其最大度最小,聚类系数也较大。改进无标度网络和局域世界网络的最大度较大,但前者降低经典BA 网络最大度的效果优于后者;二者的聚类系数、特征路径长度、网络直径和平均介数都小于其他网络,改进无标度网络的最大介数最大。小世界电网和时空演化网络的聚类系数较大,其余特性位于云南电网与改进无标度网络、局域世界网络之间。图1 为5个网络的度分布图,度分布p(k)表示度为k 的节点所占比例,即等于度为k 的节点数/节点总数。相比其他4 个网络,云南电网度为1 的节点所占的比例最小,度为2 和3 的节点比例最大。改进无标度网络、局域世界网络和小世界电网的度为1的节点占45 %左右,时空演化网络度为1 的节点的比例也大于35%。以上分析表明,不同的电网发展演化方式得到的网络的统计特性存在较大的差异,即网络结构存在较大的差异,这可能影响其鲁棒性。

图1 复杂网络度分布p( k)Fig.1 Degree distributions p( k) of complex networks
2 鲁棒性分析
网络中少数元件故障后,能量传输的路径将发生变化,引起负荷在剩余节点中重新分布,可能导致部分节点因过负荷而被移除;过负荷节点被移除后将引起新一轮的负荷重分配和节点移除,此过程将继续循环,直到网络中剩余节点的负荷都小于其容量。本文根据Motter 和Lai 提出的连锁故障模型[12],以节点介数定义负荷,认为节点的容量Ci正比于其初始负荷Li(0),Ci=T·Li(0),i=1,2,… ,n(n 为节点总数;T 为耐受系数),模拟单一元件故障诱发连锁故障传播过程,分析和比较不同网络的鲁棒性差异。
为了量化单一元件故障对网络的影响,本文采用归一化故障规模Sattack(式4)、连通性水平g(式5)和相对效率R(式6)3 个评价指标,分别从网络的故障规模、连通性和性能3 个角度评估网络的鲁棒性。归一化故障规模越小,连通性水平和相对效率越大,表明网络的鲁棒性越强。

式中:Si为移除节点i 诱发的连锁故障规模;n′为故障后最大连通域中的节点数;Enorm和Efaul分别表示故障前后电网的效率,用公式7 计算,dij表示节点i 和j 之间的最短距离。

从以前的研究中知道,蓄意攻击负荷最大的节点对网络的结构和性能的影响都非常大。因此,本文分别攻击云南电网、改进无标度网络、局域世界网络、小世界电网和时空演化网络等5 个网络中负荷最大的节点,待连锁故障传播结束后,计算网络的归一化故障规模Sattack、连通性水平g和相对效率R,结果如图2 ~4 所示(除云南电网,其余网络都是20 个网络的模拟结果的平均值)。显然,随着耐受系数T 的增加,各个网络的Sattack都减小,g 和R 增大;但当T 增大到一定程度后,Sattack,g 和R 不再随T 的增加而变化。这说明适当地增加网络容量有利于提高电网的鲁棒性。图2 显示:小世界电网的Sattack最小,时空演化网络的次之;当T <1.38 时,云南电网的Sattack小于改进无标度网络和局域世界网络的;当T >1.38 时,则相反。然而,在图3 和图4 中,只有当耐受系数T <1.06 时,小世界电网的g 和R 均最大;当T >1.52时,在5 个网络中其g 最小,R 也仅略高于云南电网(5 个网络中云南电网R 最小)。还注意到,改进无标度网络和局域世界网络的g 和R 增加幅度较大,然而小世界电网的g 和R 增加幅度非常小(T 从1 增加到2 时,g 和R 的增加幅度不足0.05)。这说明:增加容量可以有效地增强改进无标度网络和局域世界网络的鲁棒性,云南电网和时空演化网络的鲁棒性也有一定程度的提高;但对改善小世界电网的鲁棒性的效果不是很明显,即不同网络的鲁棒性变化幅度存在较大的差别。

图2 网络归一化故障规模Sattack随耐受系数T 变化图Fig.2 Changes of the normalized avalanche sizes ( Sattack)in complex networks with the tolerance parameter( T)

图3 网络连通性水平g 随耐受系数T 变化图Fig.3 Changes of the relative size of the largest connected components ( g) in complex networks with the tolerance parameter ( T)

图4 网络相对效率R 随耐受系数T 变化图Fig.4 Changes of the relative efficiencies (R) in complex networks with the tolerance parameter (T)
下面分析不同网络的鲁棒性随容量增加变化幅度差异较大的原因。小世界电网的拓扑结构图(图5)显示:小世界电网中存在少数枢纽点(图5中的节点2 和5);这些枢纽节点一旦被移除,整个网络将解列为几个连通的子区域,子区域之间无法进行能量传输,有利于降低节点的负荷,遏制连锁故障进一步传播,因此故障规模较小;然而网络的连通性水平和相对效率却因网络解列而降低,且受网络自身结构限制,增大网络容量并不能防止网络解列,所以增加容量不能有效地提高小世界电网的鲁棒性。与之相反,改进无标度网络(拓扑结构如图6 所示)受到外界攻击或局部出现故障后,网络不会立即解列,剩余节点的负荷都较高。如果网络的容量较小,节点将因过负荷而依次退出运行,故障大规模传播,最终导致网络的连通性水平和相对效率大幅下降。然而,如果节点拥有足够的容量来承担增加的负荷,连锁故障就可以得到有效的控制,故障规模较小;同时网络连通性水平和效率也较高。因此,增加网络容量有助于提高改进无标度网络的鲁棒性。时空演化网络与小世界电网类似,也存在少数可以使网络解列的枢纽点,因此其鲁棒性随容量变化幅度较小。云南电网和局域世界网络的拓扑结构与改进无标度网络类似,故增加容量有助于提高它们的鲁棒性。
综上所述,网络容量和结构是影响鲁棒性的两个重要因素。在规划设计云南电网等实际电网时,应该根据网络容量大小(通常受经济因素制约)确定合理的电网结构。当容量较小时,可以依照小世界电网或时空演化网络的发展演化方法规划设计电网;当容量较大时,则可依照改进无标度网络和时空演化网络的发展演化方式设计鲁棒性较强的电网。
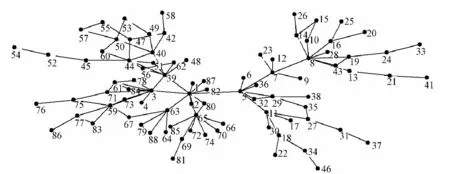
图5 小世界电网拓扑结构图Fig.5 Topological structure of a small world power grid

图6 改进无标度网络拓扑结构图Fig.6 Topological structure of an improve scale-free network
3 结 论
本文基于复杂网络理论,建立了与云南电网具有相同规模和相近连接数的改进无标度网络、局域世界网络、小世界电网和时空演化网络,对比分析了这5 个网络的统计特性,结果显示不同的发展演化方式得到的网络结构存在较大的差异。本文还着重从故障规模、连通性和性能3 个角度出发,分析了上述5 个网络对蓄意攻击负荷最大的节点的鲁棒性。分析结果表明,网络的鲁棒性不仅与其容量有关,还与其结构紧密相关。在规划设计云南电网等实际电网时,应根据容量(受经济条件制约),科学规划电网结构,尽可能地提高电网的鲁棒性。当容量较小时,可以依照小世界电网或时空演化网络的发展演化方法规划设计电网;当容量较大时,则可依照改进无标度网络和时空演化网络的发展演化方式设计鲁棒性较强的电网。
[1]韩祯祥,曹一家.电力系统的安全性及防治措施[J].电网技术,2004,28 (9):1 -6.
[2]艾欣,崔明勇,雷之力.电力系统连锁故障研究综述[J].华北电力大学学报(自然科学版),2008,35 (6):44 -51.
[3]梅生伟,薛安成,张学敏.电力系统自组织临界特性与大电网安全[M].北京:清华大学出版社,2009.10 -19.
[4]Erdos P,Rényi A.On the evolution of random graphs[J].Publ Math Inst Hung Acad Sci,1960,5:17 -61.
[5]Watt D J,Strogatz S H.Collective dynamics of ′small-world’networks[J].Nature,1998,393:440 -442.
[6]Newman M E J,Watts D J.Scaling and percolation in the small-world network model[J].Physical Review E,1999,60:7332 -7342.
[7]Barabási A L,Albert R.Emergence of scaling in random networks [J].Science,1999,286 (5439):509 -512.
[8]Liu X,LIU T Q,Li X Y.A novel evolving model for power grids [J].Science China Technological Sciences,2010,53 (10):2862 -2866.
[9]Li X,Chen G R.A local - world evolving network model[J].Physica A,2003,328 (1 -2):274 -286.
[10]曹一家,王光增,包哲静,等.一种复杂电力网络的时空演化模型[J].电力自动化设备,2009,29(1):1 -5.
[11]Mei S W,Zhang X M,Cao M.Power grid complexity[M].Beijing:Tsinghua University Press and Berlin Heidelberg:Springer-Verlag,2011.133 -160.
[12]Motter A E,Lai Y C.Cascade-based attacks on complex networks [J].Physical Review E,2002,66(6):065102.
[13]Albert R,Albert I,Nakarado G L.Structural vulnerability of the north american power grid [J].Physical Review E,2004,69 (2):1 -4.
[14]Wang K,Zhang D H,Zhang Z,et al.An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load[J].Physica A,2011,390 (23 -24):4692-4701.
[15]Wang J W,Rong L L.Robustness of the western united states power grid under edge attack strategies due to cascading failures [J].Safety Science,2011,49(6):807 -812.
[16]Motter A E.Cascade control and defense in complex networks [J].Physical Review Letters,2004,93(9):098701.
[17]Huang L,Lai Y C,Chen G R.Understanding and preventing cascading breakdown in complex clustered networks [J].Physical Review E,2008,78 (3),036116.
[18]Hu K,Hu T,Tang Y.Cascade defense via control of the fluxes in complex networks[J].Journal of Statistical Physics,2010,141 (3):555 -565.
[19]Wang J W.Mitigation strategies on scale - free networks against cascading failures [J].Physica A,2013,392 (9):2257 -2264.
[20]Wang J W.Origin of the stronger robustness against cascading failures of complex networks:a mitigation strategy perspective [J].Modern Physics Letters B,2013,27 (3):1350023.

