基于节点恢复可靠性的骨架网络重构

梁海平，顾雪平

(华北电力大学 电气与电子工程学院，河北 保定071003)

0 引 言

随着经济的发展，社会发展对电力依赖越来越强，对电力系统可靠供电的要求也越来越高。同时，随着电网规模的逐步扩大、新能源电源的广泛接入、电力市场的普遍实施、负荷的复杂程度来越来高，电力系统承受大规模停电的威胁也越来越显著。20 世纪90年代以来各国电网发生多次大停电事故，2003年一年就发生了多起大停电事故，8月14日“美加”大停电事故后，8月28日发生了英国伦敦大停电，9月1日发生了马来西亚、澳大利亚悉尼大停电，9月23日发生了瑞典和丹麦大停电，9月28日发生了意大利全国大停电［1，2］，这些大停电事故的密集出现引起了人们的普遍重视和广泛关注。通过加强电网建设，改进监管手段在一定程度上可以降低事故概率，但无法从根本上避免大停电事故的发生。作为电力系统安全防御的重要措施之一，对系统发生大面积停电后的“黑启动”问题进行研究具有重要意义［3，4］。

黑启动是电力系统恢复控制的一种极端情况，它涉及系统控制运行的诸多方面。随着大停电事故的频繁发生，上世纪90年代以来国外学者开始对黑启动问题进行试验和建模仿真［5，6］。国内科研人员也对黑启动方案的相关技术问题进行了相应的研究［7～13］，包括黑启动方案制定的一般原则、发电机自励磁、操作过电压和恢复初期小系统并列运行的动态稳定性等问题。文献［14］对系统恢复控制中的网络重构问题进行了研究，它将系统重构过程划分为“串行”和“并行”两个送电阶段进行研究，给出的送电路径寻优算法具有较好的时间性。文献［15］为以恢复尽可能多的负荷操作费用最小为目标，利用蚁群算法得到了最优操作序列。

针对现有系统恢复初期骨架网络重构过程中没有计及设备投运不成功而导致恢复失败的可能性，本文提出了一种基于节点恢复可靠性的骨架网络重构策略。该策略计及系统恢复初期设备投运失败的概率，根据Monte Carlo(蒙特卡罗)方法计算各节点恢复成功的概率，然后采用Floyd 算法进行最短路径计算，进而根据目标节点恢复成功概率的高低得到恢复路径。

1 基于Monte Carlo 的可靠性求解

1.1 Monte Carlo 方法简介

Monte Carlo 方法也称为统计模拟方法，是一种基于随机数的计算方法。Monte Carlo 方法计算结果收敛的理论依据来自于大数定律，且结果渐进地服从正态分布的理论依据是中心极限定理，该方法可用于研究复杂问题。

Monte Carlo 统计模拟方法具有以下一些优点:

(1)能够直观地描述具有随机性质事件的特点;

(2)受几何条件限制小;

(3)收敛速度与研究对象的规模无关;

(4)可同时处理多个方案、计算多个未知量;

(5)近似值与真值的误差容易确定;

(6)易于编程实现。

Monte Carlo 法同样也存在着不足之处，如:计算时间与精度关系紧密，为了获得较高的精度，往往需要较长时间的计算。

在解决实际问题的时候应用Monte Carlo 方法主要有两部分工作:

(1)用此方法模拟某一过程时，需要产生各种概率分布的随机变量;

(2)用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。

1.2 基于Monte Carlo 的可靠性求解

设有5 个独立工作的元件1，2，3，4，5，它们的可靠性均为p，将它们按图1 的方式联接(称为桥式系统)

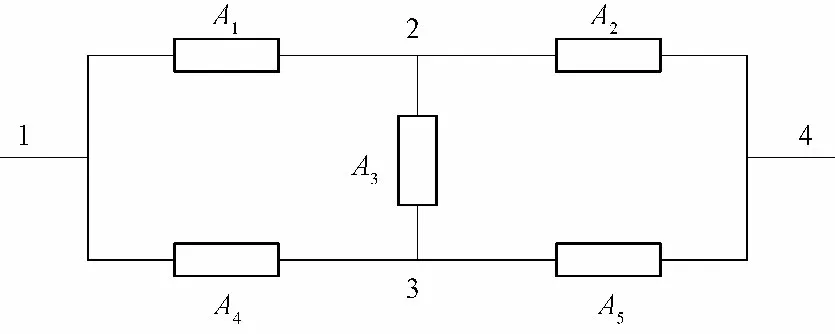
图1 可靠性计算示意图Fig.1 Diagram for reliability calculations demonstration

设A 代表“系统正常工作”;Ai(i =1，…，5 )代表“第i 个元件正常工作”。

根据概率论的知识可知图1 所示系统有4 条通路，只要其中有一条通路正常时系统就能正常工作。但并集计算过于复杂，如果把A5单独去掉，则剩下的就只是并、串联问题，因此:

式中:

如果p 为0.9，则P(A)= 0.978 5

图1 所示系统如果采用Monte Carlo 方法进行可靠性计算，采取以下步骤:

(1)产生在区间(0，1)上服从均匀分布的随机数;

(2)根据随机数确定元件的开断;

(3)判断网络1，4 之间的连通状态;

(4)记录5 000 次计算网络处于连通状态的次数，该系统某次计算的连通次数为4 891，因此其可靠性为计算过程中的1，4 之间的可靠性收敛情况如图2 所示。

图2 计算过程中可靠性收敛曲线Fig.2 Convergence curve of reliability calculation

由图可以看出，在经过若干次计算后，系统连通概率的值逐渐趋于稳定。

2 骨架网络重构的限制因素及节点恢复的可靠性

根据电力系统恢复过程中所研究问题的侧重点，将系统恢复过程划分为3 个阶段，即:黑启动阶段、网架重构阶段和负荷恢复阶段。

网架重构阶段的主要任务是尽快恢复电厂出力并使重要变电站带电，在此基础上建立一个稳定的网架，为负荷恢复奠定基础。由于网络结构、发电机出力、系统吸纳充电无功的能力、恢复过程中厂站的操作时间等多种因素的限制，网架重构过程必须有所侧重。首先，重构网络应全面地覆盖系统中的重要电源、关键变电站和必要恢复负荷;其次，参与网架重构的送电路径应具有较高的可靠性。符合上述要求的网架被称为骨架网络。

2.1 骨架网络重构的限制因素

为了尽快恢复发电厂出力，首要任务是满足发电机组辅机运行的功率需求。火电机组的恢复受到多方面因素的限制:最佳离线时间、最大临界时间、最小临界时间、机组的额定出力、机组自身的状态、机组在不同的启动条件下的启动耗时和爬坡率、系统对机组启动的限制等。

在大停电发生后，火电机组大多处于热态或是极热态，同容量、同类型的机组启动耗时一般差别不大，同时由于机组在系统恢复阶段的爬坡率受人为因素影响较大，因此，文中忽略这些因素的影响，只考虑容量和机组类型对恢复过程的影响。

我国常见的机组容量一般为200 MW，300 MW，600 MW 机组。火电机组的锅炉一般分为汽包式和直流式，而汽包式又有自然循环型和控制循环型两种，各个级别和不同类型锅炉进行配备则其再启动要求有着一定的差别。本文认为同容量、同类型的机组具有相同的启动时限，启动时间要求最迫切的同类型机组优先启动。

考虑到每个火力发电厂一般只有一台启备变，因此在系统恢复初期每个火力发电厂一次只能启动一台发电机组。

2.2 节点恢复的可靠性

大停电发生后，电力系统处于非正常状态，一些设备，如变压器、输电线路可能由于存在故障或继电保护非正常情况下的动作而造成投运失败。如果在系统恢复过程中不考虑支路投运失败的概率可能会造成恢复进程被迫中断，系统恢复过程被迫推倒重来的现象，这将在很大程度上延误系统的恢复进程。为了避免这种现象的发生，在制定黑启动方案和重构骨架网络时应对支路投运失败的概率给予足够的重视。

图3 说明了恢复路径所处的不同网络结构可能对节点恢复成功率造成的影响。假设每条支路投运成功的概率都是一样的，对于图3(a)和图3(b)中所给出的恢复路径S-A-B-C，考虑到支路投运失败时，图3(b)的节点C 明显比图3(a)中的节点C 具有更高的恢复成功率。这是因为，图3(a)的路径中的任意一条线路存在故障，恢复过程将被迫中止，而图3(b)路径中的线路如果投运失败可以通过其他线路转带来继续恢复进程，如恢复到BC 线路时BC 线路出现故障，可以通过路径BE-C 继续恢复进程，最终实现节点C 的恢复。反映到可靠性方面，图3(b)中C 节点恢复的可靠性要比图3(a)中A 节点恢复的可靠性高。

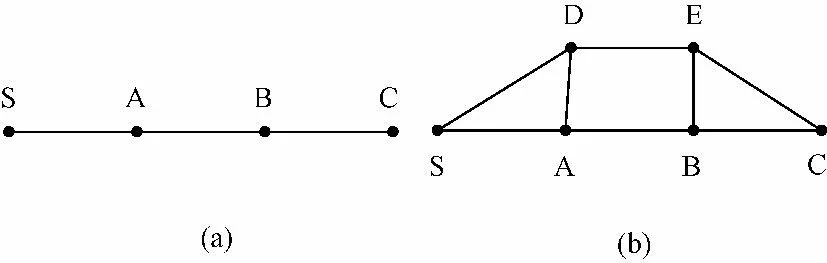
图3 路径比较Fig.3 Path comparison

支路投运成功的概率越低，将节点恢复可靠性用于确定网架重构时节点恢复顺序的效果越显著。如图3(a)，如果所有线路恢复的成功概率都是1，节点A，B，C 恢复可靠性是没有区别的，其恢复成功的概率都是1;如果所有线路恢复的成功概率都是0.5，此时其结果将会大不同，节点A 恢复成功的概率P(A)= 0.5，节点B 恢复成功的概率P(B)= 0.5 ×0.5 = 0.25，节点C 恢复成功的概率P(C)= 0.5 ×0.5 ×0.5 = 0.125 。

3 基于节点恢复可靠性的骨架网络重构

3.1 节点可靠性计算的算法流程

本文中，节点恢复时的可靠性采用蒙特卡罗方法进行计算，算法流程如图4 所示。

图4 节点可靠性流程图Fig.4 Flow chart of nodes restoration reliability calculation

3.2 骨架网络重构算法描述及流程

网络重构在某种程度上取决于节点被恢复的顺序，节点的恢复顺序受到多方面因素的影响，如负荷要求的迫切程度、恢复路径的可靠性、节点在网络中的地位等。本文采用节点恢复成功的概率作为确定节点恢复顺序的标准，在节点的恢复顺序被确定后，采用Floyd 算法计算待恢复节点到带电区域的最短路径，由此可得恢复网架，算法流程如图5 所示。

图5 骨架网络重构流程图Fig.5 Flow chart of skeleton-network reconfiguration

4 算法应用实例

为验证所提方法的有效性，本文利用MATLAB 编程实现了骨架网络重构算法，并选择IEEE30 节点系统作为算例进行了测试。系统接线如图6 所示，包含30 个节点，41 条支路，其中节点以不带方框的数字表示，支路以带方框的数字表示。设定各条支路恢复成功的概率均为0.9。假设节点1 为黑启动电源，不失一般性，假设电源2，13，22，23，27 为相同容量、相同类型的火力发电机组，因此这些机组的恢复顺序将由节点恢复的可靠性决定。

图6 IEEE30 节点系统图Fig.6 IEEE30 power system diagram

通过3 节所提算法进行节点恢复可靠性计算，排序后的结果如表1 所示。

由表1 的各节点的可靠性，可以得到电源的恢复顺序为2，22，23，13，27，此顺序与观察图直观上的感觉是有差别的。比如图6 中电源13 似乎应该优先恢复，但经过可靠性计算其可靠性要比电源22，23 差，主要是由于支路16 没有可转移的路径造成的。

表1 各节点的可靠性(排序后)Tab.1 Node restoration reliability(after sorting)

表2 IEEE 30 节点系统骨架网络重构方案Tab.2 Skeleton-network based reconfiguration schemes for IEEE 30 power system

图7 IEEE 30 节点系统骨架网络重构方案Fig.7 Skeleton-network based reconfiguration scheme for IEEE 30 power system

对于负荷节点同样可以按照此方法进行恢复。

5 结 论

本文提出了一种基于节点恢复可靠性的骨架网络重构策略。该策略采用节点恢复的可靠性用于确定节点恢复序列。在待恢复设备可能存在故障或非正常情况下继电保护动作的前提下优先恢复待恢复节点中可靠性最高的节点，从而提高系统恢复的成功率。算例证明，该策略给出的重构方案能够有效应对系统中存在故障线路而导致恢复被迫终止的问题，保证系统大停电后的顺利恢复。

［1］US－Canada Power Outage Task Force.Final report on the August 14th 2003 blackout in the United States and Canada ［R］.

［2］祝瑞金，李莉华，郑淮，等.北美历次重大停电事故的比较分析及启示［J］.华东电力，2004，32(l):18 －23.

［3］周孝信，郑健超，沈国荣，等.从美加东北部电网大面积停电事故中吸取教训［J］.电网技术，2003，27 (9):1.

［4］韩祯祥，曹一家.电力系统的安全性及防治措施［J］.电网技术，2004，28 (9):1 －6.

［5］Delfino B，Denegri G B，Invernizzi M，et al.Blackstart and restoration of a part of the Italian HV network:modeling and simulation of a field test ［J］.IEEE Trans.on Power Systems，1996，11 (3):1371 －1379.

［6］Funakoshi T，Furukawa K.Transformer overvoltage problems and countermeasures at black start ［C］.Toronto，Ontario Canada:IEEE PES General Meeting，2003.

［7］吴涛，郭嘉阳，李华伟.华北电网利用十三陵抽水蓄能电厂水电机组进行黑启动的试验研究［J］.电网技术，2001，25 (3):56 －58.

［8］张其明，王万军.陕西电网黑启动方案研究［J］.电网技术，2002，26 (4):42 －48.

［9］程改红，徐政.电力系统故障恢复过程中的过电压控制［J］.电网技术，2004，28 (11):29 －33.

［10］张玉琼，顾雪平.基于随机统计分析的黑启动操作过电压的计算校验［J］.电工技术学报，2005，20(5):92 －97.

［11］王洪涛，刘玉田，邱夕照.基于分层案例推理的黑启动决策支持系统［J］.电力系统自动化，2004，28 (11):49 －52.

［12］高远望，顾雪平，刘艳，等.电力系统黑启动方案的自动生成与评估［J］.电力系统自动化，2004，28 (13):50 －54.

［13］刘艳，顾雪平，张丹.基于数据包络分析模型的电力系统黑启动方案相对有效性评估［J］.中国电机工程学报，2006，26 (5):32 －37.

［14］周云海，闵勇.恢复控制中的系统重构优化算法研究［J］.中国电机工程学报，2003，23 (4):67 －70.

［15］Chin Hongchan，Su YuhSheng.Application of the antbased network for power system restoration ［C］.Dalian，China:2005 IEEE/PES Transmission and Distribution Conference ＆ Exhibition:Asia and Pacific，2005.