计及储能系统充放电策略的风光混合发电系统容量优化

吴晨曦，文福拴，李 梅

(1.浙江大学 电气工程学院，浙江 杭州310027;2.杭州电子科技大学 自动化学院，浙江 杭州310018;3.文莱科技大学，文莱斯里巴加湾BE1410)

0 引 言

风光混合发电系统已广泛应用于没有电网供电的孤岛等场合。由于风力发电与光伏发电的出力都随气候变化［1，2］，风光混合发电系统的规划与运行就较传统电力系统更为困难。风能和光能具有互补性，白天光能丰富，夜晚没有光能但有风能。这样，如何适当优化风光混合发电系统的容量对保证供电可靠性和降低系统投资与运行成本都有重要作用。

在风力发电系统和光伏发电系统最优容量确定及相关问题的研究方面，国内外已有一些文献［3～12］。其中，文献［3 ～6］是针对只有风力发电系统和光伏发电系统的。文献［7］采用解析法求取考虑风光发电出力随机性的若干种风光发电容量组合的供电可靠性。文献［8］用加拿大滑铁卢大学开发的WATGEN 软件(其可以由月平均气象数据生成每天每h 的气象数据)计算每h 的太阳辐射总量，并基于历史数据预测未来各h 的风速，在此基础上建立风光发电出力模型，之后研究了如何合理增加发电容量以满足负荷增长和供电可靠性的需要。文献［9 ～12］研究了在满足供电可靠性的前提下风、光、蓄的最优容量组合问题。其中，文献［12］还借助HOMER (Hybrid Optimization Model for Electric Renewable，可再生能源混合发电系统优化建模)软件将从中国气象科学数据共享网获得的月平均气象数据经离散化后得到1年8736 h的风速、光照和温度。文献［9 ～12］都没有考虑储能系统的充放电优化策略问题。

由于风力发电与光伏发电的出力随机性，单靠它们很难保证供电可靠性，一般要配备油机或储能系统(battery energy storage system，BESS)，以提供调频等辅助服务能力。BESS 作为储能装置可以平抑风光混合发电的功率波动［13］。对于由风、光、储组成的混合发电系统，在确定风电和光电的发电容量时，需要适当优化BESS 的充放电过程，这样才能得到最优的风电和光电容量。但在现有的文献中，尚缺乏这方面的研究报道。

在上述背景下，本文对风光混合发电系统的容量优化问题开展研究，并考虑了BESS 的充放电优化策略问题。首先，以某地区实际气象数据为基础分析风力发电和光伏发电的出力波动，并采用动态规划法优化BESS 充放电策略。之后，建立了在保证供电可靠性的前提下优化配置风力发电、光伏发电和储能电池容量的数学模型，并采用遍历搜索方法求解。最后，以IEEE-RBTSBUS4的配电系统为例，来说明所提出的方法的可行性与有效性。

1 风电、光电的发电功率与BESS 充放电功率

本文所讨论的风光储混合系统包括风力发电、光伏发电和BESS，整个系统结构如图1所示。

图1 风光储混合系统Fig.1 Hybrid WPG/PV/BESS system

1.1 WPG 发电功率

如果忽略风机的机械损耗，变桨恒频控制的双馈风力发电机在时刻t 风速为v(m/s)时的发电功率可用式(1)计算［2］:

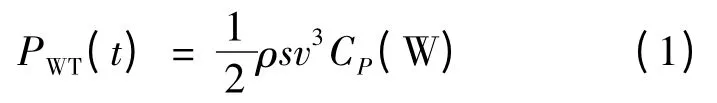
式中:PWT(t)为风机捕获的风能功率;ρ 为空气密度，kg/m3;s 为风轮扫风面积，m2;CP为风能利用系数，可由式(2)求得。

式中:

式中:θp为桨距角，当双馈风力发电机运行于次同步转速时(此时风速介于切入风速与额定风速之间)，桨距角控制系统被锁定为θp= 0，不工作。桨距角控制系统只有在超同步转速(风速高于额定风速且低于切出风速)时才工作，通过控制桨距角使双馈机发出的功率维持在额定值附近。当风速高于切出风速时风机停止运行;λ 为叶尖速比，其定义如式(4)所示。

式中:ω 为桨叶端角速度;R 为桨叶半径。当风速小于风机切入风速时，风机发出功率为0;当风速介于切入风速与额定风速之间时，θp= 0，按式(1)～(4)计算风机功率。当风速高于额定风速时，风机变桨控制系统工作，使风机发出功率在额定功率附近。当风速大于风机切出风速时，风机退出运行。

一般认为平均风速服从Weibull 分布。可用蒙特卡洛仿真法生成生成1年8 736 h(52 周)服从Weibull 分布的风速，再根据(1)～(4)式计算每h 风力发电功率。

1.2 PV 发电功率

每天日照时数S 表示一天内不同辐射强度下的累加值。全天日照辐射总量H 如式(5)所示，其描述了日照时数对日辐射量的影响。

式中:HL为进入地球大气层内的太阳辐射强度;a和b 为经验系数;SL为每天日长，h。

式中:WS为日落时角，地球自转1 周360°对应的时间为24 h，即每h 相应的时角为15°。正午为0°，上午为负，下午为正。这是式(6)计算每天日长的依据;H0为地球大气外层的辐射强度;τ 为空气透明系数，这里采用式(10)描述空气透明系数的概率密度函数［14］。

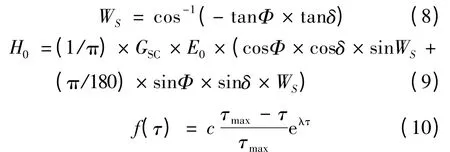
式中:Φ 为纬度;δ 为太阳赤纬角，在1年中每天的太阳赤纬角是一定的，可以查万年历获得;GSC=1.367 kW/m2为太阳常数，即进入地球大气的太阳辐射在单位面积内的总量;E0为地球轨道偏心率校正因子，其可由式(11)计算得到;τmax为空气透明系数的最大值;c 和λ 均为与τmax和空气透明系数均值τmean相关的量，可由式(12)～(14)求得。

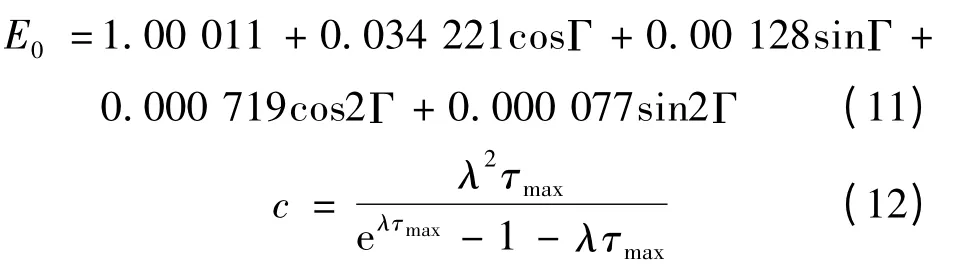
式中:Γ 为日角，Γ = 2π(l －1)/N;l 为1年中的日序数，如1月1日的日序数为1;N 表示1年的天数，润年时N=366，平年时N=365。

在已知H 的前提下，从日出到日落各个时段的辐射量占一天内总辐射量的比率可以用式(15)所描述的正态分布来模拟［15］:

式中:t ∈ 1，[ ]24 ;d0和d1均为常数。每h 的日照辐射量H(t)= R(t)H，可按式(17)折算成峰瓦时数。峰瓦时定义为当大气质量为1.5 AM (air mass)、温度为25 ℃、日照强度为1 000 W/m2的时间。

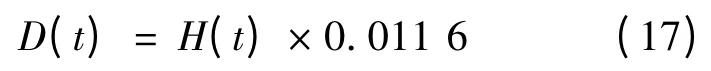
式中:D(t)为峰瓦时数，h;0.0116 为折算系数，(h·cm2/cal)。

光伏发电系统每h 的发电量可由式(18)计算:

式中:Ppeak和ηPV分别为光伏发电系统的峰瓦功率(W)和效率;WPV(t)的单位为kW·h。光伏发电系统在时刻t 的输出功率为PPV(t)= Ppeak× ηPV×D(t)。空气透明系数按式(10)所描述的概率密度函数用蒙特卡洛仿真来抽样获得。

1.3 BESS 的充放电功率

在本文中，储能设备选取钠硫蓄电池，其额定功率、额定容量和充放电效率分别用Prate(MW)，EBESS(MW·h)和ηE表示。这里以式(19)所表示的一年内等效负荷平方和最小为目标对储能系统每h 的充放电功率进行优化［16，17］:

式中:PL(t)为h 的t 负荷功率;PE(t)为BESS 的充电或放电功率，充电为正，放电为负，浮充时电池功率为0。电池充放电过程需满足下述约束条件:

式(20):表示电池各个时段的最大最小电量约束，Emin和Emax分别为最小和最大电量;EBESS为电池容量;E(t)和E(t －1)分别为不考虑电池自放电情况下t 时段和t －1 时段电池剩余电量;Δt 表示时间间隔(本文设定为1 h)。这里采用动态规划法优化电池充放电策略，首先将每个时间段的电池充放电状态划分为若干个离散状态［18］。钠硫电池可以成倍输出额定功率，但在其放电功率高于额定功率时，放电时间有所限制。充电功率范围为［0，1.2Prate］。考虑到在本文中充放电时间段以h 为单位，表1 列出了离散后的充放电状态及在不同放电功率下的可持续时间，充电功率按恒定为Prate计算。

表1 BESS 可能的状态Tab.1 Possible charge or discharge states of BESS

对于任一时间段，满足式(20)所表示的约束条件的充放电状态为该时段可能的充放电状态。这里采用动态规划方法中的顺序推解法确定电池的充放电状态。电池初始电量E(0)=0.1EBESS，第 t 小时的递推方程为 f(PE(t)) =其中PE(t)为第t 小时储能系统的充放电功率;un为第t 小时的决策变量;u(t)是由PE(t)和最大最小电量等确定的允许决策集合;vn(PE(t)，u(t))为等效负荷平方和。顺序找到式(19)的最小值后，再逆序搜索每个时段电池的充放电功率。

2 风光混合发电系统的最优容量确定方法

2.1 供电可靠性指标

采用失负荷概率PLOLP(Loss of Load Probability，LOLP)衡量风光混合发电系统供电可靠性［8］:

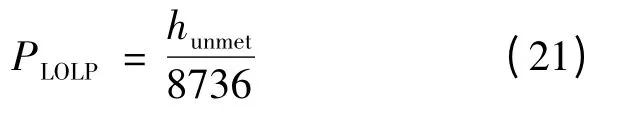
式中:hunmet表示一年中断电h 数。

2.2 优化模型

这里以WPG，PV 和BESS年费用之和最小作为风光混合发电系统容量最优配置问题的目标函数，以失负荷概率小于允许值作为约束:

式中:CWP，CPV和CB分别为风能设备、光伏设备和BESS 设备的年费用;λ 为允许的LOLP 的阈值。以风机为例，其年费用主要包括两部分:(1)折算到本年度的固定投资成本，包括设计成本、制造成本、运输成本、土地成本等;(2)年运行维护成本，如检修和管理成本等。初始投资折算到等年值的固定成本CF可按式(23)计算:

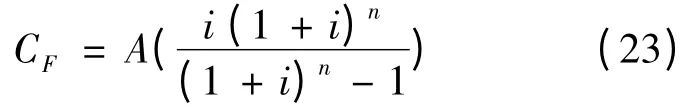
式中:A 为总投资;i 为年利率;n 为风机经济使用年限。

考虑每年的运行维护费用CM后，风机的年费用CWP可用式(24)求取。

光伏发电系统年费用计算方法与风力发电系统类似。BESS 的使用寿命与电池循环放电次数及放电深度有关，在后面的算例中将说明如何估算其经济使用年限。

2.3 优化步骤

这里采用简单的遍历搜索法求解最优风光发电容量。主要步骤如图2。

图2 确定风光发电容量最优配置流程图Fig.2 Flowchart of determining the optimal WPG and PV capacities

EBESS0为蓄电池初始容量。在求取每组风光发电容量组合的供电可靠性时，BESS 在各个时段的充放电功率按1.3 小节介绍的动态规划方法优化确定。如果给定的BESS 容量不能满足风光混合发电系统的供电可靠性要求，则需要增加储能装置的容量。在本文中，采用启发式方法给定BESS 容量的初值，如果不能满足供电可靠性，再逐步增加其容量。

3 算例和结果

3.1 参数设置

风能设备的单位固定成本为8 000 元/kW，使用寿命为20a，年运行维护费用为折算到每年的固定投资的2%;风机切入速度、切出速度、额定速度分别为3 m/s，25 m/s 和12 m/s。光伏设备的单位固定成本为12 000 元/kW，使用年限为25a，年运行维护费用为折算到每年的固定投资的1.5 %。钠硫电池固定成本为3 000 元/kW 时，年运行维护费用为折算到每年的固定投资的1 %;在放电深度为90 %和10 %的情况下，充放电循环次数可分别达到4 500 次和20 000 次;最小电量约束设置为10 %EBESS，电池容量为20 MW·h，额定充放电功率为5 MW，能量转化效率为90 %。如果不能满足供电可靠性，则逐步以ΔEBESS= 20 MW·h 的步长增加BESS 的容量。每天的日照时数从气象部门获取，风速统计数据从相关发电公司获得。

3.2 不同情况的优化结果

这里采用文献［19］给出的方法确定计算IEEE-RTS-BUS4 系统各负荷节点一年8 736 h 的功率，因为篇幅所限，这里不给出具体细节。

首先以河北省张北地区为例，求取不同场景下的优化结果。风机单机容量为1.5 MW，该地区某风场风机轮毂高度70 m 处的风速服从均值为7.5 m/s、形状系数为2 的Weibull 分布。

(1)孤岛运行方式。给定:允许的失负荷概率阈值为0.05;最小电量约束为10 %EBESS，BESS每年循环充放电1 000 次，钠硫电池寿命为10 a。优化结果为:a.57 MW 光伏发电，177 MW 风力发电，80 MW·h BESS;b.总的年费用为2.928 3×108元;3)2013年第101日为冬季非周末日(元月1日的24 个h 在年度的时序排序为2401 ～2424 时)的风力发电功率、光伏发电功率、负荷功率、BESS 充放电功率及电池的荷电状态如图3 所示;c.2013年第101日为春季非周末日(该日的24 个h 在年度的时序排序为2 401 ～2 424 时)的风力发电功率、光伏发电功率、负荷功率、BESS 充放电功率及电池的荷电状态如图4 所示。

图3 元月1日风电光电出力、负荷功率和电池充放电功率及荷电状态Fig.3 WT and PV power，load power，battery charging and discharging power，and SOC of the battery on January 1

(2)只有风力发电而不含太阳能时的孤岛运行方式。给定允许的失负荷概率阈值为0.05。优化结果为:a.392 MW 风力发电，80 MW·h BESS;b.总的年费用为4.163 4 ×108元。与前一种情况相比，风电装机容量明显增加。这是由于虽然光伏发电的固定成本相对于风力发电较高，但在日间可以提供相对稳定的发电功率;风力发电出力日间波动较大，要满足日间的较高负荷，需要安装的风力发电装机容量就非常大，这样夜间负荷低谷时的弃风较多。可见，风光混合发电较单独风力发电更经济，因为二者具有互补特性。

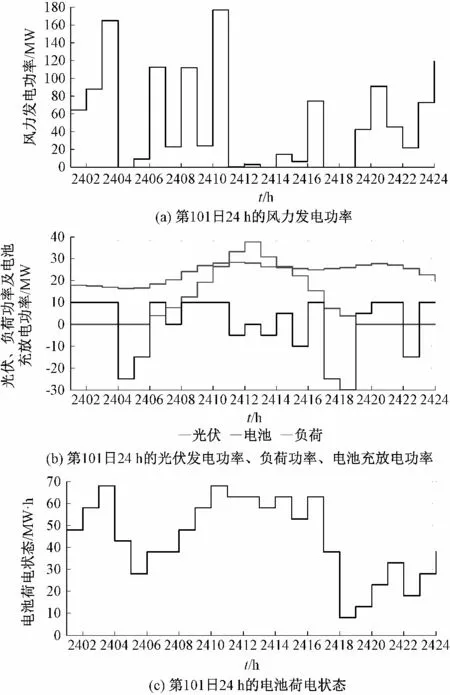
图4 第101日的风、光、负荷功率，电池充放电功率及电池荷电状态Fig.4 WT and PV power，load power，battery charging and discharging power，and SOC of the battery in the 101st day

(3)与电网的联网运行方式。假设包括风、光、储的配电系统从电网购电，功率为12 MW。优化结果为:a.风电装机容量为105 MW，光伏发电装机容量为39 MW，BESS 为40 MWh;b.年费用为1.809 2 ×108元。第107日为春季非周末日(该日的24 个h 在年度的时序排序为2 545 ～2 568 h)的风力发电功率、负荷功率、光伏发电功率、蓄电池充放电功率及蓄电池的荷电状态如图5所示。

3.3 不同气候特征的影响

不同区域的气候特征可能有明显的不同。为了分析气候特征对风光发电系统容量配置的影响，本小节以青海冷湖地区和浙江慈溪地区为例做进一步的计算比较，并针对风光发电系统孤岛运行方式进行。

图5 第107日的风、光、负荷功率，电池充放电功率及电池荷电状态Fig.5 WT and PV power，load power，battery charging and discharging power，and SOC of the battery in the 107th day

青海冷湖地区的风能资源和太阳能资源较张北地区更为丰富，前者的年平均风速与年日照时数均高于后者。与张北和冷湖地区相比，浙江省慈溪地区的风光资源均较欠缺。表2 为张北、冷湖、慈溪风光资源的对比。

表2 张北、冷湖、慈溪风光资源对比Tab.2 Comparisons of wind and solar resources in Zhangbei，Lenghu and Cixi

针对青海冷湖地区的优化结果为:a.133.5 MW 风力发电，36 MW 光伏发电，BSEE 80 MW·h;b.年费用为2.5517 ×108元;c.2013年第101日系春季非周末日，风力发电功率、光伏发电功率、负荷功率、电池充放电功率及电池的荷电状态如图6 所示。

图6 青海冷湖地区第101日负荷功率，电池充放电功率及电池荷电状态Fig.6 WT and PV power，load power，battery charging and discharging power，and SOC of the battery in the 101th day in Lenghu region of Qinghai province

表3 列出了在允许的失负荷概率阈值为0.05的情形下张北地区、冷湖地区、慈溪地区风光发电系统孤岛时的风电和光伏发电的容量配置情况。从表2 可以看出，对于风光资源相对丰富的冷湖地区，优化后的年费用较少;而在风光资源相对较少的慈溪地区，年费用较高，对BESS 的容量要求较大。

表3 3 种不同情形下的优化结果Tab.3 Optimization result of three scenarios

4 结 论

本文研究了风能和光伏混合发电系统的容量优化问题，以实际气象数据为基础并考虑了风力发电与光伏发电出力的波动特性，建立了最优配置风电和光伏发电装机容量配置的数学模型。采用动态规划法优化储能电池的充放电控制策略，实现等效负荷方差最小。最后，以修改的IEEERBTS Bus 4 配电系统为例来说明所提方法的可行性与有效性，并对风光混合发电系统在孤岛运行与联网运行时、孤岛运行时3 种不同的气候特征对风电和光伏发电装机容量最优配置的影响。

［1］Dikinson W C，Cheremisinoff P N.Solar energy technology handbook ［M］.London:Butterworth，1980.

［2］Burton T，Sharpe D，Jenins N，et al.Wind Energy Handbook ［M］.Chichester:John Wiley ＆ Sons Ltd.，2001.

［3］Atwa Y M，EL-Saadany E F.Reliability evaluation for distributed system with renewable distributed generation during islanded mode of operation ［J］.IEEE Trans on Power Systems，2009，24 (2):572 -581.

［4］Billinton R，Bipul K，Karki R，et al.Unit commitment risk analysis of wind integrated power systems ［J］.IEEE Trans on Power Systems，2009，24 (2):930 -939.

［5］Moharil R M，Kulkarni P S.Reliability analysis of solar photovoltaic system using hourly mean solar radiation data ［J］.Solar Energy，2010，84 (4):691 -702.

［6］Antonios G M，Minas C A，Petros S D.A correlation index to evaluate impact of PV installation on Joule losses ［J］.IEEE Trans on Power Systems，2011，26(3):1564 -1572.

［7］Tina G，Gaglino S，Raiti S.Hybrid solar/wind power system probabilistic modeling for long-term performance assessment ［J］.Solar Energy，2006，80 (5):578 -588.

［8］Billinton R，Karki R.Capacity expansion of small isolated power systems using PV and wind energy ［J］.IEEE Trans on Power Systems，2001，16 (4):892 -897.

［9］艾 斌，杨洪兴，沈 辉，等.风光互补发电系统的优化设计［J］.太阳能学报，2003，24 (5):718 -723.

［10］Diaf S，Diaf D，Belhamel M，et al.A methodology for optimal sizing of autonomous hybrid PV wind system［J］.Energy Policy，2007，35 (11):5708 -5718.

［11］Hocaoglu F O，Gerek O N，Kurban M.A novel hybrid(wind/photovoltaic)system sizing procedure ［J］.Solar Energy，2009，83 (11):2019 -2028.

［12］徐林，阮新波，张步涵，等.风光蓄互补发电系统容量的改进优化配置方法［J］.中国电机工程学报，2012，32 (25):88 -98.

［13］丁明，徐宁舟，毕 锐.用于平抑可再生能源功率波动的储能电站建模及评价［J］.电力系统自动化，2011，35 (2):66 -72.

［14］Hillands K G T，Huget R G.Probability density function for the clearness index with applications ［J］.Solar Energy，1982，30 (3):195 -209.

［15］Jain P C.Comparison of techniques for the estimation of daily global irradiation and a new technique for the estimation of hourly global irradiation ［J］.Solar and Wind Technology，1984，1 (2):123 –134.

［16］鲍冠南，陆 超，袁志昌，等.基于动态规划的电池储能系统削峰填谷实时优化［J］.电力系统自动化，2012，36 (12):11 -16.

［17］傅英定，成孝予，唐应辉.最优化理论与方法［M］.北京:国防工业出版社，2008.

［18］徐宁舟.电池储能电站静动态功能研究及其效益评估［D］.合肥工业大学，2011.

［19］IEEE Committee Report.A reliability test system.IEEE Trans on Power Apparatus and Systems，1989，4 (3):1238 -1244.