基于改进小生境帝国竞争算法的多目标电力系统无功优化

张金环，安海霞，王永春

(1.天津职业大学 机电工程与自动化学院，天津300410;2.长春市热力集团，吉林 长春130022)

0 引 言

电力系统无功优化就是应用数学优化的方法，科学、合理地对电力系统无功进行调配以满足电力系统运行的各项安全、经济指标。对电力系统进行无功优化是提高电压质量、降低网损的有效手段。调节发电机和调相机的无功出力、控制已装设的并联电容器和电抗器的投切组数、调节有载调压变压器的分接头档位等措施可以在已有的负荷水平下，优化调节电力系统无功资源，从而尽可能在保证电力系统运行电压质量的条件下，达到运行网损最小的目标。尤其是近年来引入的电力经济市场机制，使得电力公司的经济效益问题日益凸显，这就对电网运行的稳定性和可靠性、用户侧的电能质量和预防电网事故发生和扩大等提出严格要求，而这些措施都以电力系统的无功优化为前提，无功优化使得电力系统的运行更加安全、稳定和经济［1～3］。

常用的无功优化求解算法主要有两大分类，分别是常规的优化算法和具有现代启发式的优化算法。常规的数学优化算法(如内点法［4］、梯度法［5］、线性规划［6］和二次规划［7］等)存在对初值要求高、要求目标可微、容易产生维数灾和求解时间长等不足［8］。具有现代启发式的优化算法(如遗传算法［9，10］、免疫算法［11，12］和粒子群算法［13，14］)虽然可移植性好、原理简单、搜索能力强，但仍容易出现陷入局部收敛和早熟现象等。文献［15］中引入一种自适应的遗传优化算法，结合基于实数进行编码的混合优化算法来处理离散－连续的数学优化问题;文献［16］提出一种求解控制策略，把内点法和遗传算法进行交替使用，求解离散子优化问题和连续子优化问题，该方法的优点是能够提高计算效率;文献［17］引入一种预先设定个体间距离和可调适应度的进化小生境，但该方法是建立在先验知识的基础上，导致其利用效率不高;文献［18］采用帝国竞争算法(imperialistic competition algorithm，ICA)对电力系统供需侧联合随机调度模型进行求解，但该算法需要依赖先验知识，收敛速度较慢，搜索能力较弱。

本文提出一种改进小生境帝国竞争算法(improved niche imperialistic competition algorithm，INICA)，在该算法的迭代过程中，小生境内的国家通过动态聚类方法结成联盟，以实现联盟内部竞争度共享，而不再依赖单个国家的先验知识;引入最优个体相邻搜索和区域小生境国家联盟共享机制等提高算法收敛速度和计算速度;构建了多目标电力系统无功优化模型，通过改进小生境帝国竞争算法对模型进行求解。仿真算例中与现有求解算法相比，所提方法能够有效地避免普遍存在的全局收敛问题，从而对算法的搜素效率有所提高，以期对无功优化问题提出一种新的解决思路。

1 多目标无功优化模型

多变量多约束的非线性问题在解决电力系统无功优化问题中是不可避免的。在电力系统有功负荷、电源及系统网架条件给定的情况下，以容性或感性的无功补偿容量、变压器变比和发电机的机端电压作为控制变量，状态变量则选取PQ 节点电压幅值和发电机的无功出力，在满足电力系统无功负荷需求的情况下，综合考虑全网网损和状态变量的越限情况，分别选用电压安全稳定裕度指标最高，有功网损指标最低和电压偏移量指标最小为主要的技术性指标。建立无功优化的多目标函数如式(1):

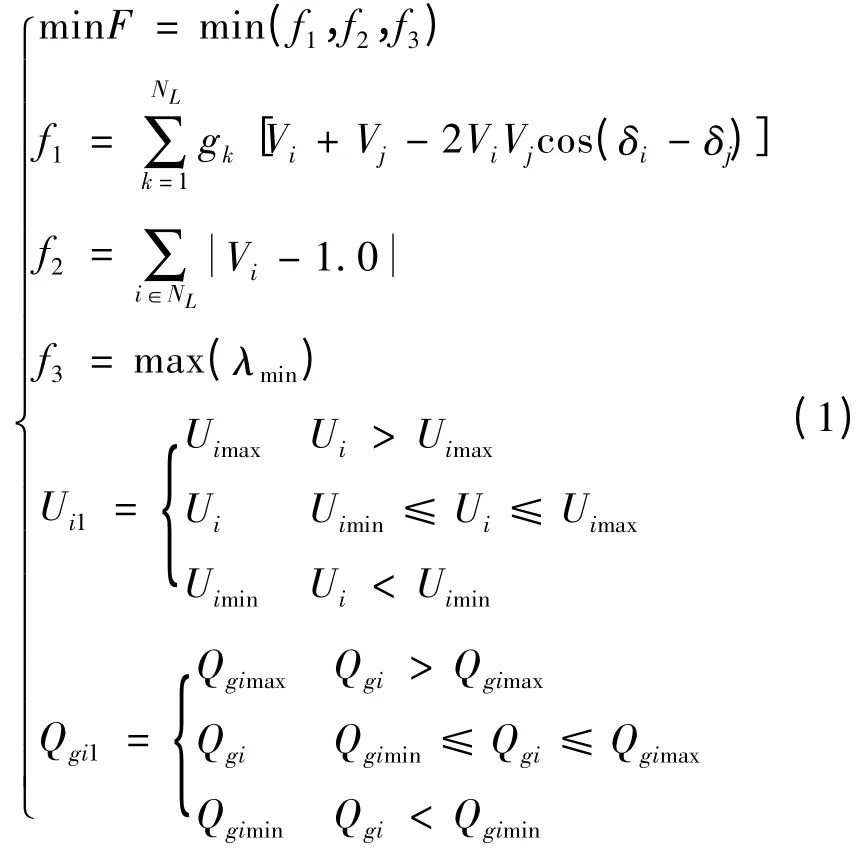
式中:f1表示系统网损;f2表示电压偏差;f3表示电压稳定裕度;NL表示负荷节点数;λmin表示系统电压稳定裕度指标;gk表示支路k 的电导;δi，δj分别表示对应节点的电压相角;Vi，Vj为支路k 两端节点电压;Uimax，Uimin和Qgimax，Qgimin分别为对应变量的上下限;Qgi，Ui分别为发电机无功功率和负荷节点电压。

电压稳定裕度指标由文献［19］给定，该指标由潮流方程即负荷节点的功率特性和网络特性决定，反映了节点电压波动的相对大小，反映所研究节点的无功储备能力，本文取所有节点中的最大值作为指标，单个节点的表达式为

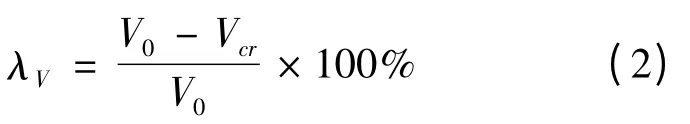
式中:V0和Vcr分别为负荷节点在当前状态和临界状态下的电压;λV为单个节点的电压稳定裕度指标。

等式约束条件和不等式约束条件共同组成电力系统无功优化的两个约束条件。大量文献资料中常用的等式约束条件为

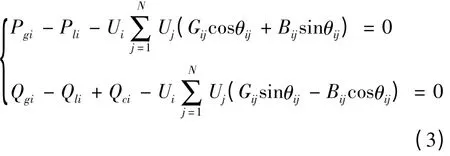
式中:N 为系统节点数;θij，Gij和Bij分别为节点i，j 之间的电压相角差、电纳和电导;Qci为无功补偿功率;Qli，Pli分别为负荷的无功功率和有功;Pgi为发电机的有功功率。

常用的不等式约束为

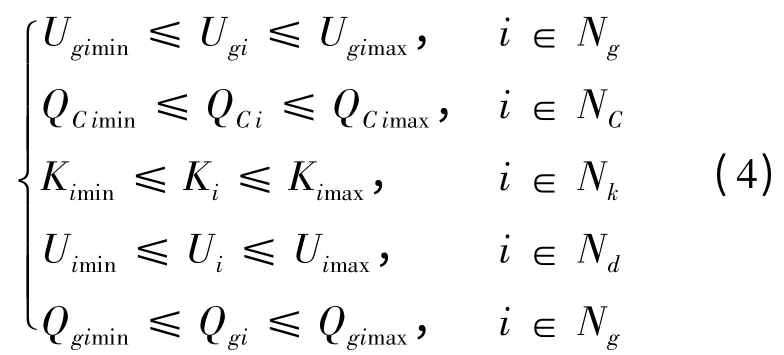
式中:Nd，Nk，NC和Ng分别为负荷节点数、有载变压器数、无功补偿装置数和系统发电机节点数;Ugimin，Ugimax，QCimin，QCimax和Kimin，Kimax分别为对应量的上下限;Qgi，Ui分别表示两个状态变量，即发电机无功功率和负荷节点电压;Ki，QCi和Ugi分别表示3 个控制变量，即给定的有载变压器特定变比、电力无功补偿装置的实际配置容量以及并网发电机的机端电压。

2 改进小生境帝国竞争算法

2.1 小生境帝国竞争算法

与其他进化算法具有一定的相似性，小生境帝国竞争算法定义的初始种群个体被称为国家，国家又被分为帝国和殖民地两类，它们的权利大小不同。迭代过程中，首先形成一系列的小生境国家联盟，使用小生境形成技术得到不同国家的竞争程度;其次建立国家共享机制，调整每个国家联盟中不同国家的竞争力;最终形成联盟内部和联盟与联盟之间的竞争环境。

该算法是一种全局性优化的进化算法，借鉴了人类政治社会殖民阶段国家之间竞争并最终占领殖民地的过程。

第1 阶段:帝国形成。国家由h 维决策变量组成country = ［x1，x2，…，xh］，国家的函数值用fcountry表示，第n 个国家的标准化权利定义为

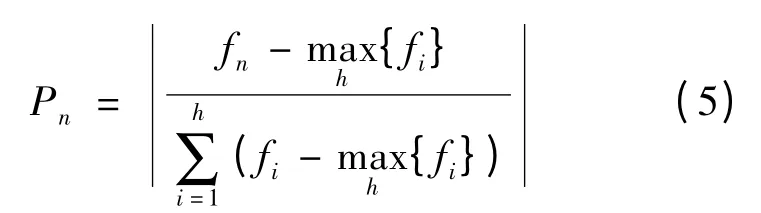
式中:i 表示第i 个国家。

第2 阶段:吸收殖民地。假设每块殖民地移动的距离l 服从均匀分布l ～U(0，δ×lD)，帝国周围的殖民地逐渐向帝国靠近。其中，δ ＞1，lD为殖民地与帝国之间的距离;帝国与殖民地移动方向之间的连线偏移夹角为θ，服从分布θ ～U(- ψ，ψ)，其中，ψ 为偏移夹角调整系数。

第3 阶段:帝国竞争。帝国的总权利值定义为

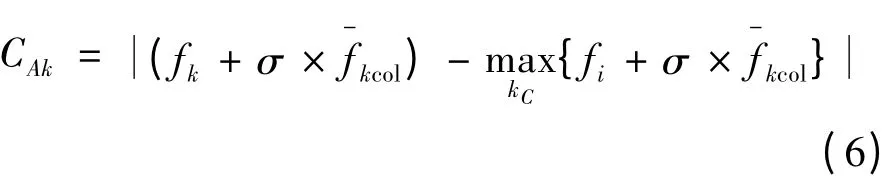
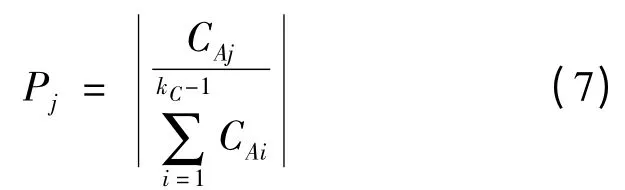
第4 阶段:帝国消亡。经过帝国之间的相互竞争之后，权利较小的帝国所拥有的殖民地会被权利比其强大的帝国侵占，当殖民地全部被占领后则该帝国就会自动灭亡，在算法中消除其位置。当各个帝国之间的竞争结束时，有且仅有一个帝国建国，且其余所有殖民地均被该帝国侵占，此时算法迭代停止并得到最优解;否则，返回2)。

2.2 国家联盟的动态聚类与竞争度共享技术

为了实现国家联盟的形成，采用模糊动态聚类方法实现。将1 个包括M 个n 维个体的国家联盟记为Xi= ［xi1，xi2，…，xin］(i = 1，2，…，M)。模糊动态聚类形成国家联盟遵循以下步骤:

(1)归一化处理各个国家个体不同量纲的变化范围;

(2)采用最值法确定关系矩阵，基于个体Xi和个体Xj的模糊相似关系，进而得到相似系数Rij，其表达式如式(8):

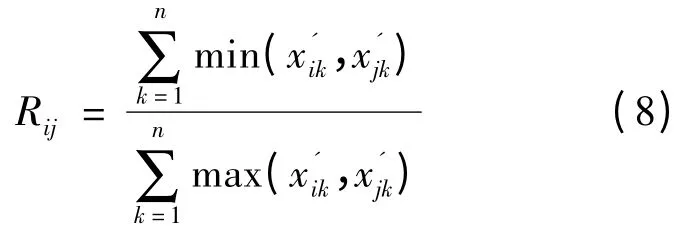
(3)动态聚类国家群体，对相似度系数λ(0 ＜λ ≤1)进行调整。相似度系数由式(8)确定:

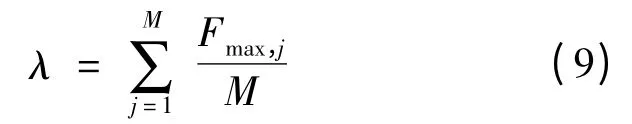
此步骤遵循以下过程:

从i = 1 时开始动态聚类分析国家联盟中的第1 个国家;当λ ≤Rij(j = i +1，i +2，…，M)时，Xi与Xj被认为是同一类型的国家个体;依次选取i = i +1，当已经对Xi进行了归类后，则将迭代计算转至下一步，当没有归类Xi后，则所做的聚类分析需要按照上上一步中的方法;重复上一步，直到聚类分析完最后一个国家个体。最终动态调整每次迭代中的相似度，从而聚类划分成若干国家联盟。

通过反映个体间相似程度的共享度来调整群体中个体的竞争度，该技术可以很好的维护群体的多样性。群体个体之间的密切程度用共享函数表示，它们之间的关系属于正向型。共享度Si表示国家个体与国家联盟内其他各个体之间共享函数的和。)

式中:S(dij)表示共享函数。

在得到群体中各个体的共享度后，还需要调整各个体的竞争度。

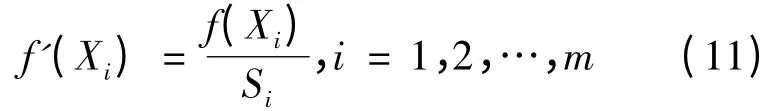
式中:f(Xi)为个体Xi共享前的竞争度函数;f′(Xi)为个体Xi共享后的使用度函数。

联盟中的相似国家个体通过以上技术就可以很大程度上提高自身的竞争力度，从而避免了在迭代计算过程中若干相似个体被重复选择的可能性，算法的局部收敛和早熟问题得以解决。

2.3 改进算法的步骤

本文所提改进算法主要结合了当前主流的竞争度共享技术和聚类分析方法，整个算法的改进计算过程如下:

(1)初始化程序参数，生产初始随机国家联盟，并计算各国家个体的竞争度。初始群体记为

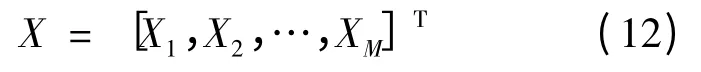
(2)对群体X 进行帝国形成、吸收殖民地、帝国竞争度运算，在此基础上，形成新的国家联盟X′并计算其国家个体的竞争度。

(3)当国家联盟中出现竞争力最大的国家时，将其作为超级大国保留至到下一步迭代计算;

(4)竞争度共享运算，调整各国家个体的竞争度;

(5)判断终止条件。若满足终止条件，则计算结束并输出计算结果;若不满足终止条件，则跳转至步骤(2)，重新迭代计算。

改进小生境帝国竞争算法在无功优化问题的求解过程中，按照如图1 的步骤进行。

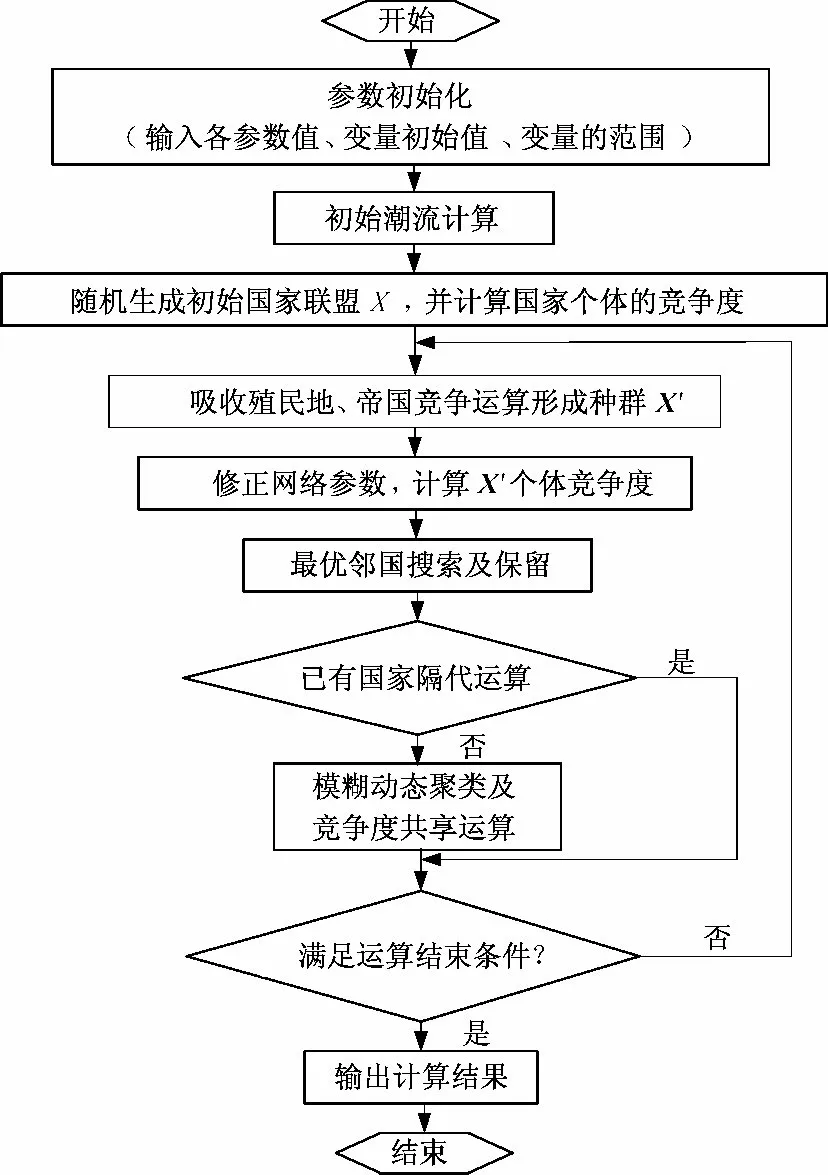
图1 基于INICA 的算法流程图Fig.1 Algorithm flow chart based on INICA

3 算例分析

为了验证本文所提算法和无功优化方法的有效性，对IEEE－30 和IEEE －57 节点测试系统进行编程仿真，仿真软件采用Matlab7.0。

3.1 IEEE-30 节点系统

测试系统的节点和支路数据及拓扑结构图详见文献［20］。该测试系统中有负荷节点21 个，发电机节点6 个，支路共有4 条。其中，节点1 设定为优化计算中的平衡节点，PV 节点设定为4，7，14，16 和19 节点，剩余节点为平衡节点［21］。取系统的基准容量为100 MVA，初始国家数为150，初始帝国数为20 个，δ = 1.75，σ = 0.2，ψ = π/2 。网络中各变量的选取范围参见文献［22］。网络初始系统总有功负荷Pl= 2.846 p.u.，无功负荷Ql= 1.273 p.u.;初始有功网损Ploss= 0.048 768 p.u.。

选用遗传算法(genetic algorithm，GA)、帝国竞争算法(ICA)和本文改进小生境帝国竞争算法(INICA)进行比较，对所提算法进行有效性验证。优化计算50 次，取其收敛结果最优值作为最终的计算结果，如表1 和表2 所示，各变量单位为标幺值单位(p.u.)。

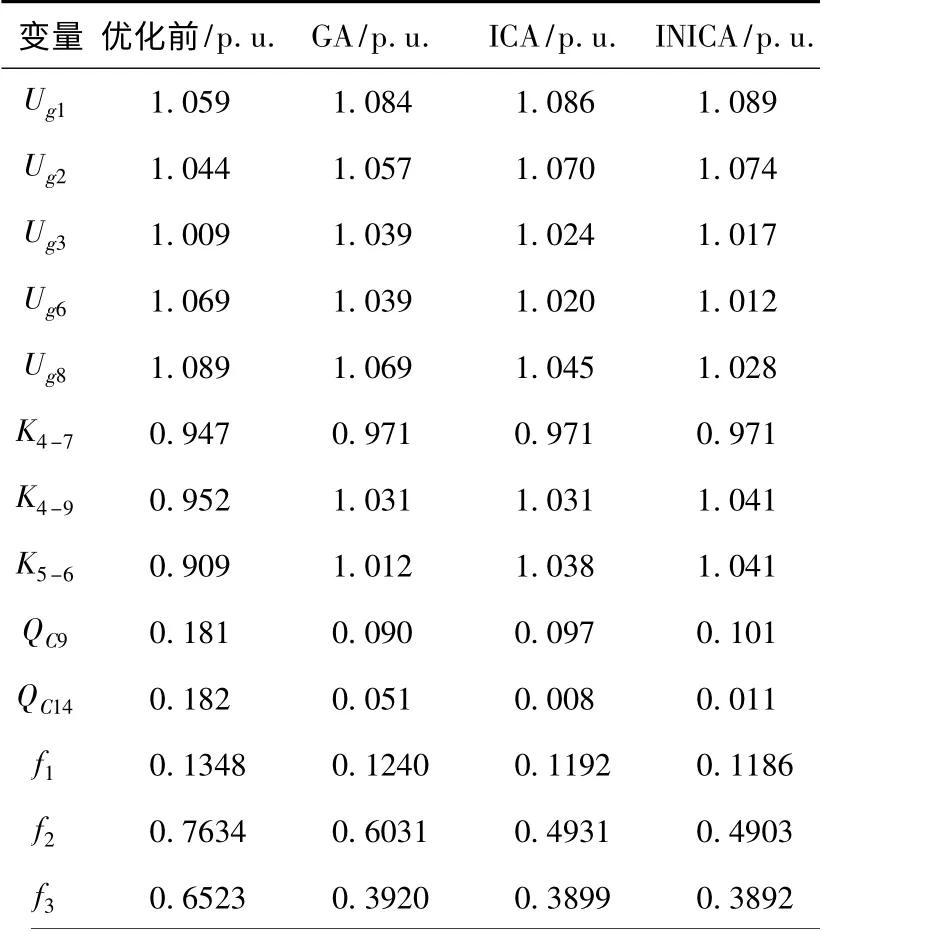
表1 3 种算法的变量优化结果对比Tab.1 Variable optimization results comparison of three kinds of algorithms

由表1 可知，ICA 和INICA 的变量优化结果比较接近，且均比GA 效果好，但INICA 的优化效果更为理想。GA 优化后系统的网损降低8.01 %，而ICA 优化后网损降低为11.57 %，INICA 优化后系统的网损降低12.02 %;电压偏差越接近于0表明电能质量越好，由f2的数据可知，INICA 的优化结果较其他两种方法占优;电压裕度指标越小系统越稳定［23］，由f3的数据可知，INICA 的优化结果较其他两种方法也是占优的。

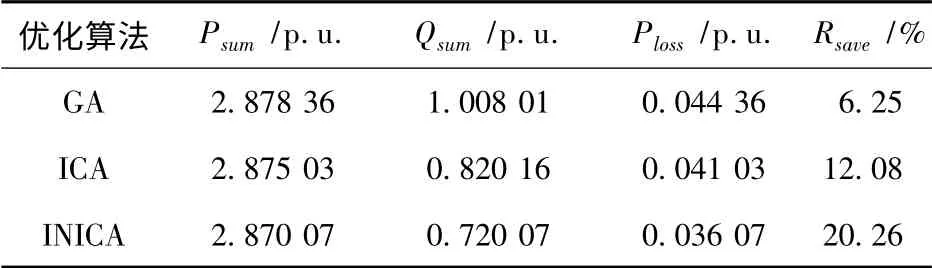
表2 3 种算法的优化结果对比Tab.2 Optimization results comparison of three kinds of algorithms

表中:Psum，Qsum为节点注入功率，Rsave为网损下降率。从表1 中可以看出，采用GA 和ICA 算法得到的系统网损分别为0.044 和0.041，而采用本文INICA 算法的网损下降为0.036;采用GA 和ICA算法得到的网损下降率分别为6.25 %和12.08%，而采用本文INICA 算法的网损下降率为20.26%，优化结果比其他两种算法更有优势。

为了验证INICA 算法的性能，选取3 种算法分别对目标函数各优化计算80 次，优化的结果如表3所示。其中，平均网损指标指的是80 次迭代中所有收敛迭代结果的平均值，单位为标幺值单位(p.u.)。3 种算法系统网损变化曲线如图2 所示。

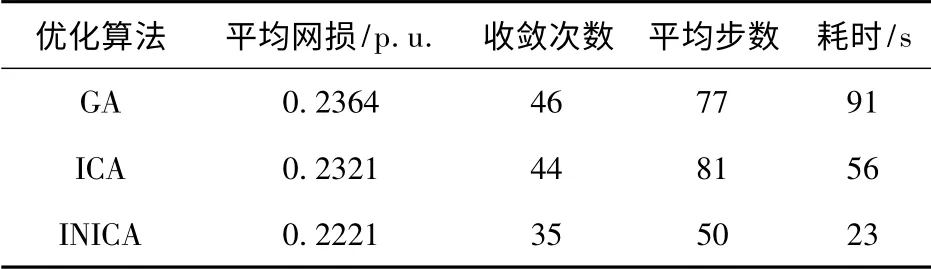
表3 3 种算法的性能比较Tab.3 Performance comparison of three kinds of algorithms

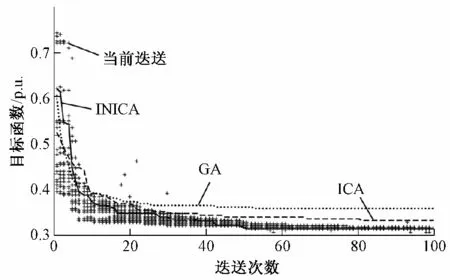
图2 IEEE－30 节点系统的无功优化收敛曲线Fig.2 Reactive power optimization convergence curve of IEEE－30 nodes system

从表3 和图2 可以看出，3 种优化算法最终都能收敛到一个最优解。尤其是在15 次之前的迭代过程中，收敛速度都较快，其中INICA 算法收敛速度最快;在随后的深入寻优过程中，GA 算法和ICA 算法的稳定迭代次数分别为80 次和70 次，而本文INICA 算法约在50 次左右就已经迭代到了稳态值，说明其具有更快的全局寻优能力。从计算耗时上来看，INICA 算法比其他两种算法分别节省了约68 s 和33 s，搜索速度最快。因此，相比其他两种算法，本文算法的全局寻优能力和搜索速度都得到了较好验证。

3.2 IEEE-57 节点系统

选取经典IEEE－57 节点系统进行仿真，对比仿真 前后各个指标的计算结果，表4 中优化后系统网损和电压越限个数均有较大幅度的减少。

表4 IEEE-57 节点系统计算结果Tab.4 Calculation results of IEEE－57 nodes system

从表4 中可以看出，采用GA 和ICA 算法得到的系统网损分别为1.145 4 和1.081 1，而采用本文INICA 算法的网损下降为1.036 1;采用GA 和ICA 算法得到的网损下降率分别为7.38 % 和14.57 %，而采用本文INICA 算法的网损下降率为22.39 %，优化结果比其他两种算法更有优势。

图3 为IEEE－57 节点系统3 种算法在收敛速度上的比较。可以看出，简单遗传算法进化到150 代左右时陷入了局部最优解，而改进小生境帝国竞争算法有效地避免了早熟，最终在100 次迭代后收敛到全局最优解。

对两个测试系统进行20 次独立计算，结果如表5 所示。可以看出，该算法每次基本都可以收敛到最优解，系统节点越多相应的迭代次数也会增多，但最终均能满足求解的范围。

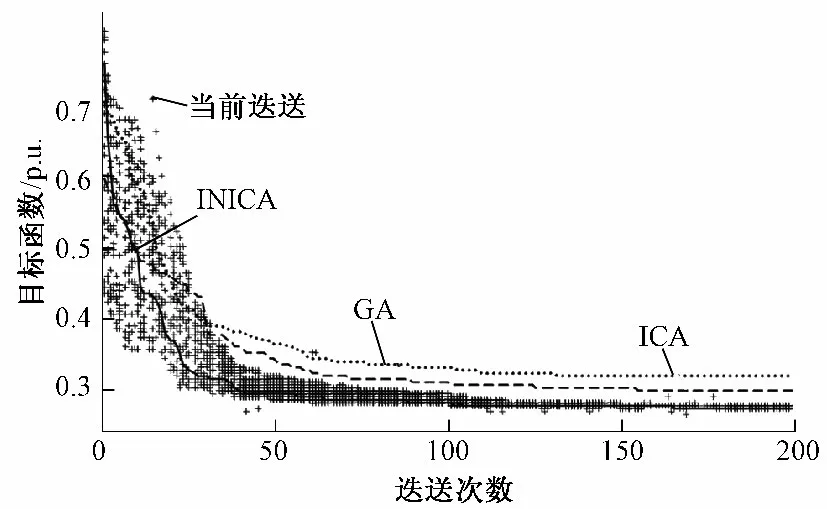
图3 IEEE－57 节点系统的无功优化收敛曲线Fig.3 Reactive power optimization convergence curve in IEEE－57 nodes system

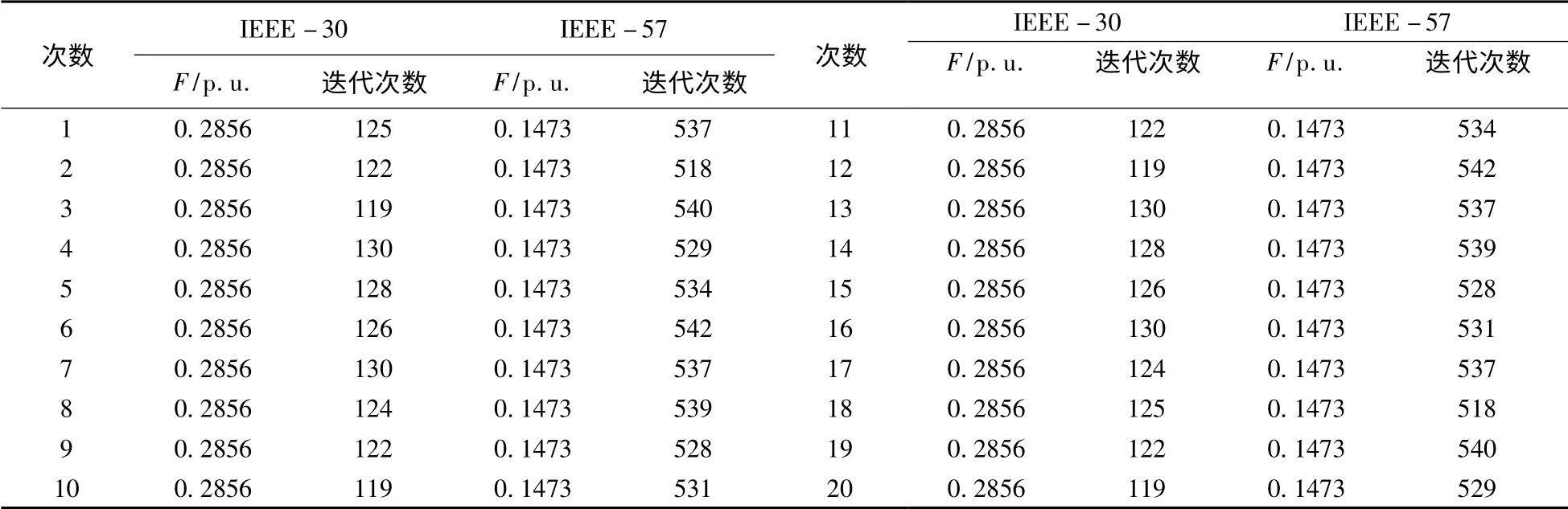
表5 20 次独立运行的仿真结果Tab.5 Simulation results of the independent operation within 20 times

4 结 论

本文提出了一种基于改进小生境帝国竞争算法的电力系统无功优化方法。算法首先需要对所有国家进行结盟，采用动态聚类分析法进行划分，进而得到国家个体的竞争度，在此基础上，采用竞争度共享技术对联盟内的国家进行竞争度共享，最终实现提高全局搜索能力的目标。选用了两个经典无功优化模型进行优化仿真计算，验证了本文所提方法的优越性，以期对电力系统无功优化问题解决方法提供一定的借鉴价值。

［1］崔挺，孙元章，徐箭，等.基于改进小生境遗传算法的电力系统无功优化［J］.中国电机工程学报，2011，31 (19):43 －50.

［2］邱晓燕，张子健，李兴源.基于改进遗传内点算法的电网多目标无功优化［J］.电网技术，2009，33(13):27 －31.

［3］张晓辉，卢志刚，秦四娟.基于改进细菌群体趋药性算法的电力系统无功优化［J］.电网技术，2012，36 (2):109 －114.

［4］柳进，常修猛，柳焯.内点法在偶对潮流优化中的应用［J］.电力系统自动化，2007，31 (5):29 －33.

［5］丁明，张晋波，汪兴强.提高预处理共轭梯度法计算大型电网潮流时并行性能的方法［J］.电网技术，2008，32 (13):15 －19.

［6］Delson J K，Shahidehpour S M.Linear programming applications to power system economics ［J］.Planning and operations，IEEE Transactions on Power systems，1992，7 (3):1155 －1163.

［7］徐建亭，王秀英，李兴源.电力系统电压无功的序列二次规划算法［J］.电力系统自动化，2001，25(23):4 －7.

［8］刘佳，李丹，高立群，等.多目标无功优化的向量评价自适应粒子群算法［J］.中国电机工程学报，2008，28 (31):22 －28.

［9］Lee Kwang Y，Bai Xiaomin，Park Y M.Optimization method for reactive power planning by using a modified simple genetic algorithm ［J］.IEEE Transactions on Power Systems，1995，10 (4):1843 －1850.

［10］Ma Xin，Liu Ruilan.Reactive power optimization in power system based on improved niche genetic algorithm［C］.International Conference on Computer Design and Applications.Qinhuangdao: IEEE，2010.413 －416.

［11］王秀云，邹磊，张迎新，等.基于改进免疫遗传算法的电力系统无功优化［J］.电力系统保护与控制，2010，38 (1):1 －5.

［12］熊虎岗，程浩忠，李宏仲.基于免疫算法的多目标无功优化［J］.中国电机工程学报，2006，26(11):102 －108.

［13］周鑫，诸弘安，马爱军.基于多种群蚁群算法的多目标动态无功优化［J］.电网技术，2012，36(7):231 －236.

［14］王韶，周鑫.应用层次聚类法和蚁群算法的配电网无功优化［J］.电网技术，2011，35 (8):161 －167.

［15］Subbaraj P，Rajnarayanan P N.Optimal reactive power dispatch using self － adaptive real coded genetic algorithm ［J］.Electric Power Systems Research，2009，79 (2):374 －381.

［16］Yan Wei ，Liu Fang ，Chung C Y，et ，al.A hybrid genetic algorithm:interior point method for optimal reactive power flow ［J］.IEEE Transactions on Power Systems，2006，21 (3):1163 －1168.

［17］向铁元，周青山，李富鹏，等.小生境遗传算法在无功优化中的应用研究［J］.中国电机工程学报，2005，25 (17):48 －51.

［18］杨楠，王波，刘涤尘，等.计及大规模风电和柔性负荷的电力系统供需侧联合随机调度方法［J］.中国电机工程学报，2013，33 (16):63 －69.

［19］张国华，张建华，彭谦，等.电网安全评价的指标体系与方法［J］.电网技术，2009，33 (8):30 －34.

［20］张勇军，任震，钟红梅，等.基于灾变遗传算法的无功规划优化［J］.电力系统自动化，2002，26(23):29 －32.

［21］马玲，于青，刘刚，等.基于量子差分进化算法的电力系统无功优化［J］.电力系统保护与控制，2013，41 (17):39 －43.

［22］Wu Q H，Cao Y J，Wen J Y.Optimal reactive power dispatch using an adaptive genetic algorithm ［J］.Electric Power Energy Systems，1998，20 (8):563 －569.

［23］李如琦，李芝荣，王维志，等.基于差分策略的多目标电力系统无功优化［J］.电网技术，2012，36(12):170 －175.