交直流互联系统对电流差动保护的影响分析及对策

申洪明，黄少锋，费 彬

(华北电力大学 新能源电力系统国家重点实验室，北京102206)

0 引 言

随着高压直流输电(high voltage direct current，HVDC)的迅速发展，交直流混合输电电网在我国已逐步形成。HVDC 在实现远距离、大容量、非同步电网互联等方面具有独特优势［1～3］。但交直流互联系统使得交流侧故障过程中出现了许多新的电气特征，这对交流电网的继电保护产生了重大影响。

文献［4］在电磁暂态框架下研究交直流系统相互影响机理和交流故障特征的变异机理，给出了暂态功率倒向的计算模型和方法;文献［5］通过开关函数法分析了换相失败情况下直流系统注入交流电网等值工频及工频变化量电流的特性;文献［6］分析了换相失败对突变量选相元件的影响;文献［7 ～9］详细分析了换相失败对纵联差动保护、距离保护和纵联方向保护的影响;文献［10］以一起误动事故为例详细分析了换相失败对交流侧继电保护的影响，特别是对纵联方向保护的影响。上述文献虽然很好的分析了交直流互联系统换相失败对继电保护的影响，但并没有提出相应的措施，而且对于连接开关站和逆变换流站的线路缺乏相应研究。

本文首先详细分析了仅发生交流侧故障时直流系统等值工频变化量电流的特征，然后将交直流互联系统分成3 部分，详细探讨了仅发生交流侧故障时对与直流系统直接相邻的交流系统电流差动保护的影响。分析结果表明仅发生交流侧故障时对稳态量的电流差动保护影响最大。并提出了仅基于幅值判据的防范措施。最后基于PSCAD/EMTDC 仿真验证了分析结果的正确性。

1 直流系统等值工频变化量电流ΔIdc.eq1的暂态特性分析

图1 为交直流互联系统等值电路图，对于逆变侧受端交流系统而言，直流系统可以等效成一个由逆变站交流侧母线电压控制的受控电流源［8］。图中idc.eq为考虑无功补偿等装置时流入交流系统的直流系统等值电流。

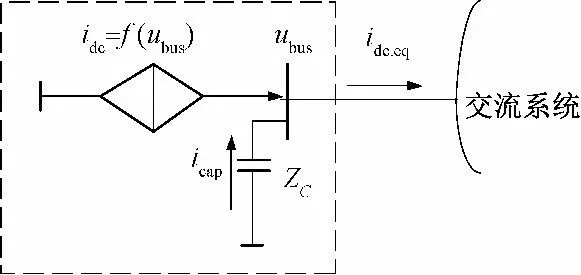
图1 交直流互联系统等效图Fig.1 Equivalent diagram of AC/DC interconnected system

图1 中idc为逆变器交流侧等值电流，icap为流过交流滤波器及无功补偿装置的电流，ubus为交流母线电压。当下标出现1 时，表示对应的工频分量，如idc1表示逆变器交流侧等值工频电流。

交流侧故障发生后直流系统的暂态响应主要分为不引发换相失败和引发换相失败两类。当交流侧故障引发换相失败时，文献［7 ～9］已经对直流系统等值工频变化量电流ΔIdc.eq1的暂态特性进行了详细的研究，研究结果表明:换相失败期间ΔIdc.eq1的幅值和相角都会发生显著的变化，从而对交流侧继电保护产生不利影响。下面重点分析交流侧故障不引发换相失败时ΔIdc.eq1的暂态特性。

图2 所示为正常稳态时的A 相电压及阀电流波形，其中相电流以流入交流系统为正，此时逆变器交流侧等值工频电流Idc1和交流相电压U1的相位差φ 为［1］

图2 正常运行的电压电流波形Fig.2 Waveform of voltage and current under normal operation

式中:β 为越前触发角;μ 为换相角。

显然正常运行时，Idc1超前于相电压U1，若以相电压U1为基准，则Idc1位于第一象限。需要指出的是，由于直流受端一般靠近区域电网的负荷中心，因此逆变侧通常采用全补偿的无功补偿方式［5］，则正常运行工况下的Idc.eq1与U1可视为同相位。正常运行时的电压电流关系矢量图如图3所示。

图3 正常运行时的电压、电流相量图Fig.3 Phase diagram of voltage and current under normal operation

当交流侧故障发生时，由于逆变侧直流电压随交流电压的降低而减少，因此直流电流必然有一个逐渐增大的过程，与此同时由于电流增大和换相电压的降低使换相角μ 也随之增大［1］。逆变器通常采用定γ 角控制，将有:

式(2)中:Δμ 为换相角的变化值;β′ 为换相失败后的越前触发角。

由式(1)、(2)可得故障发生后Idc.1超前相电压的角度为

因此，Idc1超前相电压的角度将增大，因而在相角方面，此时Idc1将逆时针转过Δμ/2 的电角度。由于没有引发换相失败，所以直流电流变化有限，Δμ 数值理应较小;与此同时，由于换流母线电压降低，无功补偿电流Icap.1也将相应减小，因此Idc.eq1转过的角度也较小;在幅值方面，由于没引发换相失败时换流母线压降十分有限［11］，所以低压限流环节VDCOL 仍然将直流电流稳定在额定值附近，因此Idc.eq1的幅值变化不大。综上所述可以看出，仅发生交流侧故障时Idc.eq1的幅值和相角变化都不大，所以造成了等值工频变化量电流ΔIdc.eq1较小，如图4 所示。由于对交流母线电压U1扰动很小，所以可以认为U1的相角不变。图4中I′

dc.eq1表示仅发生交流侧故障时直流系统等值工频电流。理论上讲，I′dc.eq1的幅值在故障暂态过程中可能大于或小于Idc.eq1，下面分情况进行讨论:

图4 未发生换相失败时ΔIdc.eq1 的变化Fig.4 Change of ΔIdc.eq1 under AC faults without causing commutation failure

需要指出的是，对于继电保护Ⅰ段而言，通常要求动作速度在30 ms 以内，对于未引发换相失败的交流故障，由于直流控制的作用将呈现先增大后减小的变化趋势，但在保护I 段时间内，一般大于即属于上述情形(1)，如图5所示。其中图5 是CIGRE HVDC 标准模型中设置B 相在0.5 s 发生150 Ω 过渡电阻接地故障得到的，t0为故障时刻。

图5 等值工频电流的变化曲线Fig.5 Change curve of equivalent power frequency current

2 交直流互联系统对电流差动保护的影响分析

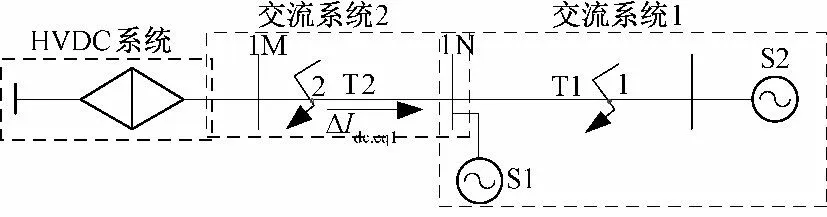
图6 交直流互联系统图Fig.6 The diagram of AC/DC interconnected network

图6 表示的是简化的交直流互联系统图，为了便于说明问题，将交直流互联系统分为3 部分:HVDC 系统，交流系统1 和交流系统2。对于交流系统2 而言，通常线路T2 很短，一般用来连接开关站和换流站;而在交流系统1 中T1 为长距离的输电线路［8］。对于T1，T2 而言，在区外故障时显然电流差动保护能准确判断，因此主要考虑区内故障受直流馈入的影响。在仅发生交流侧故障时，由于ΔIdc.eq1很小，因此对交流系统1 而言，此时HVDC 系统与正常运行时差异不大，因此当交流系统1 中发生F1 内部故障时，此时电流差动保护影响不大;考虑到T2 为短线路，所以此时两侧同步问题并不突出，因此一般都要配置差动保护作为短线路的主保护。但在交直流互联系统中，对于交流系统2 而言，如果发生F2 内部故障，此时两侧感受到的电气量差异很大，此时对差动保护的影响就会十分突出，下面重点分析交流系统2仅发生内部故障时对电流差动保护的影响。

2.1 故障分量的电流差动保护的影响分析

为了分析交流系统2 电流差动保护在交直流互联系统中的动作行为，将图6 等效为图7，如图7所示。

图7 等效电路图Fig.7 Equivalent circuit

图7 中ZLM表示M 侧保护安装处到故障点F的阻抗;ZLN表示N 侧保护安装处到故障点F 的阻抗;ZSN表示系统N 的系统阻抗。

输电线路中电流差动保护在实际应用中为了确保在外部故障时保护不误动，通常采用具有制动特性的保护判据。同时为了克服全电流差动保护在重负荷高阻抗情况下灵敏度不足的问题，还利用故障分量电流实现差动保护，其判据如下

式中:ΔIM，ΔIN分别表示M 侧和N 侧工频电流的故障分量;k 表示制动系数，k 的取值并无一个确定的值。但由于基于故障量的电流差动保护消除了负荷分量的影响，因此为了提高保护的灵敏性，相对于稳态量而言可以将制动系数降低;但同时考虑到故障量的计算可能引入误差，为了确保保护不误动，又需要将制动系数在稳态量的基础上提高一些，根据现场制动系数的整定情况，k 一般可取0.3 ～1.0。仅发生交流侧故障时虽然没有引发换相失败，但也会引起直流系统相应控制的调节，即HVDC 系统表征出了类似于故障的扰动源。由于换流站电力电子器件的非线性及直流控制保护系统的快速调节，在此暂态过程中，直流系统电气量处于时刻变化之中，但对于一个给定的时间窗，总可以将其分解为基波和各次谐波分量之和，即ΣIdceq.n，因此若将直流系统视作一个外部故障电源，且仅就其中的工频量进行分析，则整个受端网络仍可以视为线性的，它在故障时的暂态响应仍然可以按照叠加原理求得，因此可以把图7 分解成图8 所示的3 种系统状态的叠加。图中表示故障前短路点处空载电压，显然与相电压U1同相位，IL表示正常运行下的负荷电流。

图8 叠加等效电路图Fig.8 Superposition circuit diagram

由图8 可以得到:

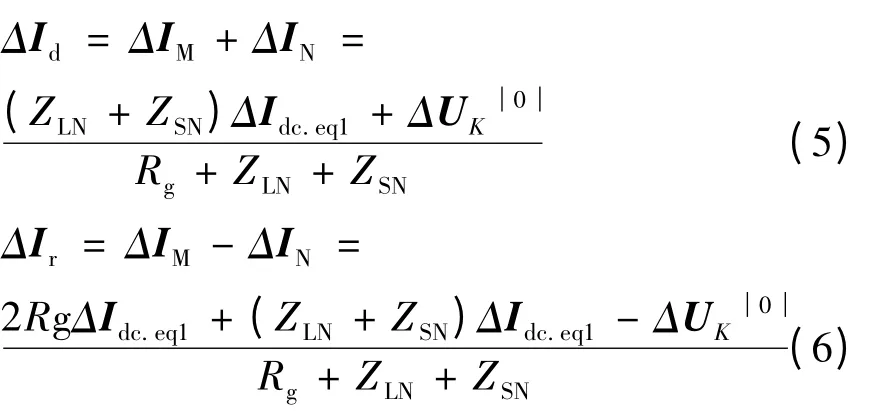
对于动作量ΔId而言，由于是短线路，并且ΔIdc.eq1较小，所以一般情况下(ZLN+ ZSN)ΔIdc.eq1对于制动量ΔIr而言，由于Rg数值较为可观(短线路下发生故障并没有引发换相失败，意味着过渡电阻比较大)，所以此时2RgΔIdc.eq1不能忽略，此时(5)、(6)进一步化简为

通过式(7)可以看出，在故障形式一定的情形下，此时动作量一般比较稳定，波动较小;通过第1部分的分析可知，由于交流侧发生故障但未引发换相失败的暂态过程中一 般 大 于因此ΔIdc.eq1与U1之间的夹角一般小于90°，另外由于随着Idc.eq1逆时针转动的过程中增大，所以制动量也会逐渐增大，一旦大于动作量，就会引发保护的拒动。

2.2 稳态量的电流差动保护的影响分析

由故障分析理论可知，故障分量加上负荷分量即稳态量。此时稳态量的动作量跟故障分量的动作量相同，而制动量增加了2IL，此时基于稳态量的电流差动保护可以写为

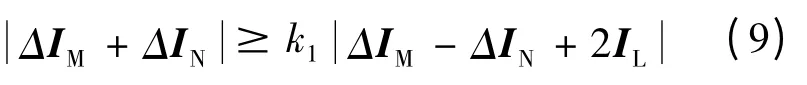
式中:k1表示制动系数，一般取0.5 ～0.7。

与故障分量判据相比，稳态量判据只是在制动量中增加了2IL。通过第1 节的分析可知，ΔIdc.eq1的幅值较小，所以ΔIM幅值较小，同时考虑到大过渡电阻情况下ΔIN大小也非常有限，因此负荷电流的加入会大大增加制动量的大小，非常容易造成动作量小于制动量，造成保护的拒动。

2.3 减少保护区内故障拒动的措施

传统的电流差动保护实际上利用了电流的幅值和相角特征来识别区内故障和其他工况。在交直流互联系统而言，保护一侧连接等值直流系统，另一侧连接的是交流系统，无论交流侧故障是否引发了换相失败，由于直流控制的原因，此时两侧电流的幅值差异很大，而且与故障位置无关。另一方面，无论是正常运行还是区外故障，两侧电流的幅值几乎相等，即IM/IN≈1。考虑到测量误差等因素的影响，可以取K = IM/IN∈(0.95，1.05)。当幅值的比值K 位于该区间以外时，则判为区内故障。即新的差动保护的判别逻辑如图9 所示。

图9 新的保护判别逻辑Fig.9 New protection logic

新的判别逻辑不仅限于交流系统2，对任何位置的受端系统都成立。新的判据可能无法做到在任何工况下都能准确动作，但至少比单一的利用传统保护判据的性能有所提高。

3 仿真验证

3.1 模型说明

利用PSCAD/EMTDC 搭建如图7 所示的仿真模型，图中直流系统采用国际大电网会议CIGRE的HVDC 标准模型，受端交流系统短路比SCR =4.4，线路MN 全长为20 km，参数为:r1=0.025e－3(Ω/m)，x1=0.3e－3(Ω/m);r0=0.075e －3(Ω/m)，x0=0.9e－3(Ω/m)。采样频率4 000 Hz，所有故障均设置在0.5 s 发生，持续时间为0.05 s。为了在最极端的情况下保证保护动作的可靠性，稳态量判据和故障量判据的制动系数分别取为0.7 和1。

3.2 基于故障量的仿真分析

图10 故障分量仿真结果Fig.10 Simulation results of current differential protection based on fault component

图10 是在线路中点经120 Ω 过渡电阻发生A相接地故障下形成的仿真分析图。图10(a)表示的是动作量和制动量的大小;图10(b)表示的是动作量和制动量的比值;图10(c)表示的是故障后的大小。由图10(c)可以看出，此时所以ΔIdc.eq1与之间的夹角小于90°，因此制动量随着数据窗的移动越来越大，如图10(a)虚线所示。同时由于动作量几乎保持不变，从而使得两者的比值越来越小，如图10(b)中在0.525 s 后两者的比值将小于1，可能低于整定的制动系数而造成保护的拒动。

3.3 稳态量的仿真分析

图11 是在线路15 km 处发生经150 Ω 过渡电阻A 相接地故障时计及负荷分量的动作电流Id与制动量Ir的实际值及两者的比值。由图11(a)可以看出此时制动量远大于动作量，从而使得制动系数远小于整定值0.7，如图11(b)所示，因此将造成保护的拒动。

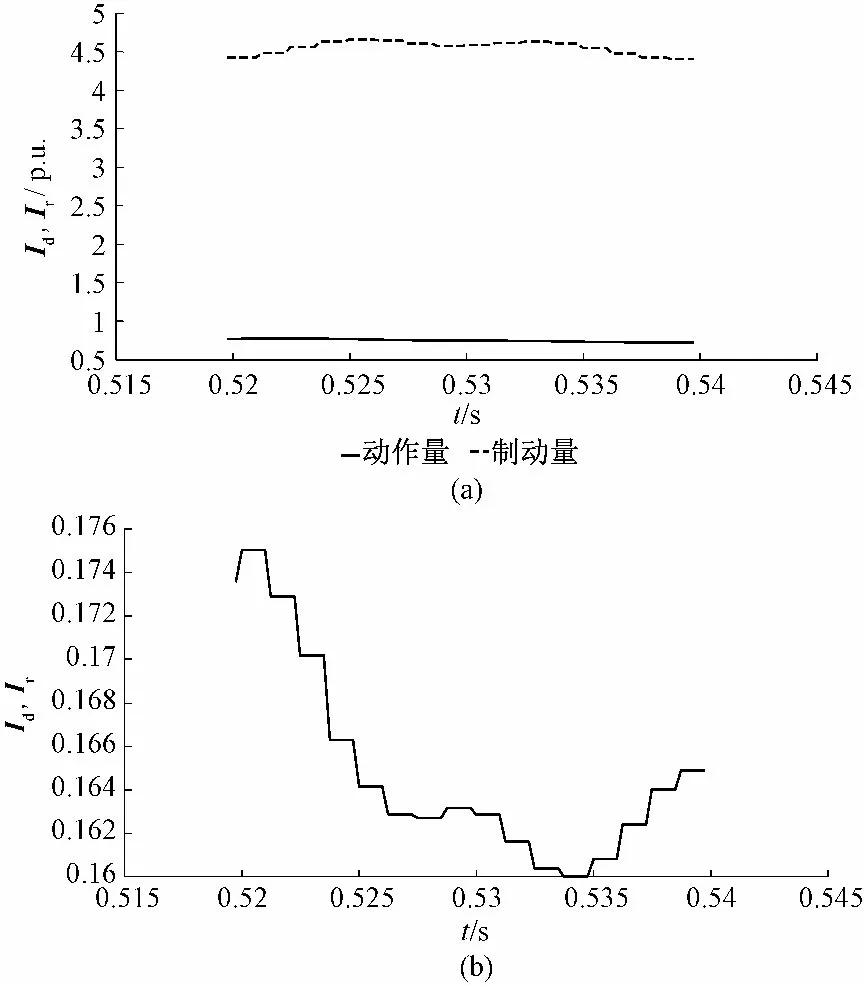
图11 稳态量仿真结果Fig.11 Simulation results of current differential protection based on steady component

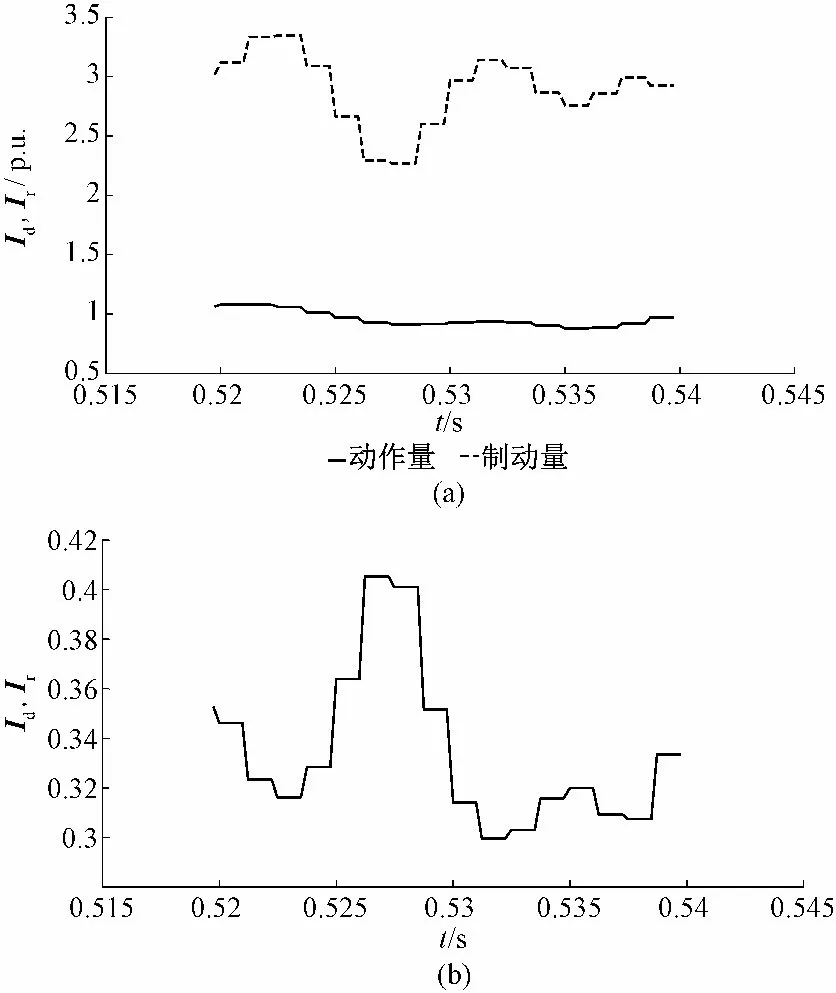
图12 稳态量仿真结果Fig.12 Simulation results of current differential protection based on steady component

图12 是在线路15 km 处发生经100 Ω 过渡电阻A 相接地故障形成的仿真图形，此时恰好未引发换相失败故障。由图12(a)可以看出此时制动量仍远大于动作量，从而使得制动系数远小于整定值0.7，从而造成保护的拒动。

通过图11 与图12 的仿真结果可以看到，交流侧发生故障但未引起换相失败时，对于与直流系统直接相连的输电线路，稳态量差动保护的制动量要远大于动作量，容易导致保护拒动。

3.4 防范措施的仿真分析

图13(a)、(b)故障类型与图11，12 相同。此时两侧电流幅值的比值IM/IN∉(0.95，1.05)，所以判为内部故障，新的判据能可靠动作。

图13 幅值判据仿真结果Fig.13 Simulation results of the amplitude criterion

4 结 论

本文对交直流互联系统下输电线路电流差动保护进行了详细的分析，可以得出如下结论:

(1)仅发生交流侧故障，即使未引发换相失败，也会对电流差动保护的稳态量判据和故障量判据产生影响，其中对稳态量判据的影响最为严重。因此在交直流互联系统中采用差动保护作为短线路的主保护并不可靠。

(2)随着数据窗的移动，基于故障量的电流差动保护中的动作量变动不大，但制动量可能会增大，导致保护的灵敏性逐渐降低。仅利用两侧幅值作为新的辅助判据，可以有效的提高差动保护的动作性能。

［1］浙江大学直流输电科研组.直流输电［M］.北京:水利电力出版社，1985:181 －182.

［2］刘济豪，郭春义，刘文静，等.基于改进换相面积的直流输电换相失败判别方法［J］.华北电力大学学报，2014，41 (1):15 －21.

［3］蔡泽祥，朱浩骏，白雪峰，等.多馈入直流输电系统的动态特性及稳定性控制与分析［J］.华北电力大学学报，2004，31 (5):1 －8.

［4］李晓华，蔡泽祥，黄明辉，等.交直流电网故障暂态功率倒向解析［J］.电力系统自动化，2012，36(10):61 －67.

［5］刘俊磊，王钢，李海峰，等.HVDC 系统换相失败对交流电网继电保护影响的机理分析［J］.中国电机工程学报，2013，33 (19):111 －119.

［6］张健康，索南加乐，焦在宾，等.交直流混联电网突变量选相元件动作性能分析［J］.电力系统自动化，2011，35 (17):76 －80.

［7］张璞，王钢，李海峰，等.直流馈入下的输电线路电流差动保护动作特性分析［J］.电力系统保护与控制，2010，38 (10):1 －5.

［8］张璞，王钢，李海峰.直流馈入下的输电线路距离保护动作特性分析［J］.电力系统自动化，2012，36 (6):56 －62.

［9］李海锋，张璞，王钢，等.直流馈入下的工频变化量方向纵联保护动作特性分析［J］.电力系统自动化，2009，33 (9):41:46.

［10］邵震，王炳炎.直流输电换相失败对交流侧继电保护的影响［J］.高电压技术，2006，32 (9):42 －45.

［11］C V Thio，J B Davies，K L Kent.Commutation failures in HVDC transmission systems［J］.IEEE Trans.Power Del，vol.11，No.2，pp:946 －957，April 1996.

［12］刘强，蔡泽祥，刘为雄，等.交直流互联系统暂态功率倒向及对继电保护的影响［J］.电力系统自动化，2007，31 (7):34 －38.