基于混沌搜索的AMPSO-BPNN在光伏功率预测中的应用研究

张建成，李 倩，周春霞，庞春江，丁晓哲

(1.华北电力大学 电气与电子工程学院，河北 保定071003;2.唐山供电公司，河北 唐山063500;3.中国电力科学研究院，北京100192)

0 引 言

太阳能是一种清洁、绿色、可持续利用的新能源，且光伏发电是太阳能的一种有效利用方式。燃而光伏发电系统的输出功率具有不确定性和波动性，大规模光伏发电系统并网运行会影响电力系统的安全、稳定、经济运行。如何更加准确地预测光伏发电系统的输出功率，进而采取有效的应对措施是学术界和工程界关注的焦点［1～5］。

常见的光伏功率预测方法有很多，如回归模型预测法、时间序列预测法、支持向量机预测法、灰色预测法、人工神经网络预测法等。文献［6］将BP 神经网络模型引入太阳能逐时总辐射预测中，模型的预测效果优于美国ASHRAE、ARIMA 等太阳逐时辐射模型;文献［7］基于气象数据和同期太阳总辐射数据，按照天气类型，采用不同修正因子，对未来一天逐时太阳总辐射进行了预测;文献［8］建立了基于支持向量机回归的光伏发电功率预测模型，实现对未来一天整点时刻的功率预测，但建模过程中未考虑同一天气类型下辐照强度、温度等因素对光伏功率的影响;文献［9］分析了光伏阵列的输出特性，建立了基于最小二乘支持向量机的光伏功率预测模型，但建模过程中对气象因素的处理不够精细，预测精度还有待提高;文献［10］利用粒子群优化BP 神经网路，建立了基于PSO-BP 神经网络的短期光伏功率预测模型，虽对BP 网络有所改进，但PSO 算法仍存在一定的局限性，预测算法还有待完善。

本文针对BP 神经网络和PSO 算法的不足，利用混沌序列的随机性、遍历性及对初值的敏感性等特点，将混沌搜索和自适应变异思想引入到粒子群算法中，提出了一种混沌搜索的自适应变异粒子群优化算法(AMPSO)以提高全局收敛的概率和速度，最终建立了混沌搜索的AMPSO-BP 神经网络的光伏功率预测模型，并利用所提模型预测光伏电站的输出功率，取得了较好的效果。

1 混沌搜索的自适应变异粒子群算法

1.1 自适应变异粒子群算法

标准PSO 算法通过跟踪个体极值和全局极值点来更新各粒子的速度和位置，更新公式如式(1)、(2)所示，但其存在着容易陷入局部极值、收敛速度慢等缺陷［11］。

式中:ω 为惯性权重;c1，c2为学习因子(r1，r2∈［0，1］分别为粒子i 在第k 次迭代中第d维的速度和位置;pk

id为粒子i 在第k 次迭代中第d维的个体极值的位置;pk

gd为种群在第k 次迭代第d维的全局极值的位置。

国内外学者从不同角度对标准PSO 算法进行了改进［12～16］，大致可分为:

(1)基于惯性权重调整策略的改进，如线性递减惯性调整策略、非线性递减惯性调整策略、随机惯性调整策略等;

(2)基于早熟判断机制的改进，如对陷入早熟的粒子进行混沌变异操作等。本文考虑从惯性权重和飞行时间两方面改进粒子更新公式，并结合个体变异策略提出了一种自适应变异粒子群算法。该算法通过动态调整惯性权重和飞行时间，能很好地平衡算法的全局搜索能力及局部搜索能力，个体变异策略又能在不影响种群深度搜索能力的前提下，很好地提升其广度搜索能力，提高了算法的收敛速度，并有效避免了粒子陷入局部极值。

惯性权重作为PSO 算法中调整全局搜索与局部搜索的重要参数，合理设置惯性权重，是避免算法陷入局部最优并高效搜索的关键［17］。采用的自适应惯性权重调整策略如式(3)所示。当粒子适应度值优于当前种群平均适应度值时，赋予粒子较小的惯性权重，以提升局部搜索能力;反之，赋予粒子较大的惯性权重，以提升全局搜索能力。

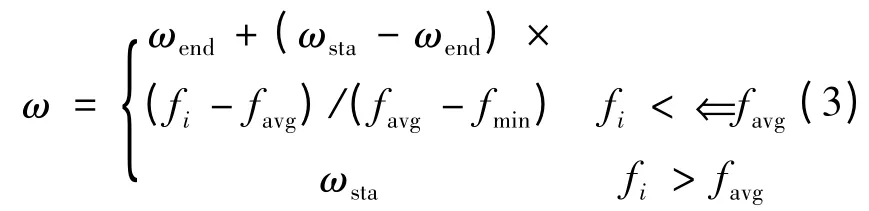
式中:fi为粒子i 的适应度值;favg为当前种群的平均适应度值;fmin为当前种群的最小适应度值。

由于迭代初期粒子离最优位置比较远，较长的飞行时间可以加速粒子向最优位置“靠拢”;而随着迭代次数的增加，粒子离最优位置越来越近，较短的飞行时间可以减小粒子“飞过”最优位置的可能性，有效地避免“振荡”现象的产生。动态的调整飞行时间能有效地解决陷入局部极值等缺点，其调整策略如式(4)所示。

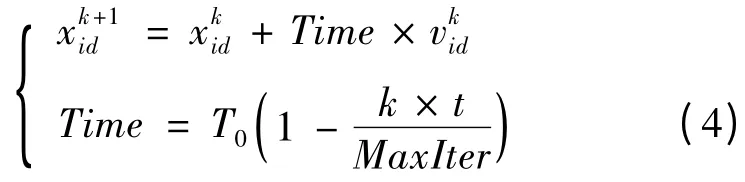
式中:Time 为粒子的飞行时间;T0为初始飞行时间(T0=0.9);k 为比例调节因子(k =0.9);t 为当前迭代次数;MaxIter 为最大迭代次数。

在PSO 的迭代过程中，常用群体适应度方差或种群在一定迭代次数内是否进化来判断“早熟”现象，相应的改进方法或是针对当前适应度值差的粒子进行变异操作，或是随机初始化种群中的部分粒子。然而当前适应度值差并不表明该粒子对种群进化的贡献小，而且随机初始化部分粒子往往会导致进化的中断，即上次寻优搜索还未完成，又要重新初始化种群，开始新的搜索。因此提出一种个体变异策略:在PSO 进化过程中记录个体的更新次数，若个体粒子更新不频繁，说明粒子所处位置较差，不会对种群全局最优值的更新做出贡献。所以，当种群在一定迭代次数内未进化时，要重新初始化更新最不频繁的个体粒子。这样把重新初始化对象由种群转为个体，既保证了种群的多样性，又防止了进化过程屡屡被中断，有效地提高算法的搜索性能。

1.2 混沌搜索策略

混沌优化算法是一种随机性的智能优化算法，由于其具有遍历性、随机性、规律性，较之其他随机性的智能优化算法获得最优解的可能性更强。为了提升PSO 算法的深度搜索能力，引入混沌搜索策略，以每代全局最优解为基点，进行k 次混沌搜索，产生k 个个体，若产生的个体粒子的适应度值由于全局最优适应度值，则替换当前种群的全局最优解。

混沌优化算法直接采用混沌变量进行搜索，混沌变量按照式(5)所示的表达式产生，且bk≠{0.25，0.5，0.75}。混沌搜索原理［18］如式(6)所示。

式中:bk为混沌变量;xgbest为每代的全局最优解;Ud，Ld为混沌搜索空间的上限和下限;Pm为变异率，通常取值0.5。

2 光伏功率预测模型的建立

2.1 光伏发电功率的影响因素分析

由于受到辐照强度、温度等气象环境因素以及光伏阵列安装位置、转换效率等地理因素的影响，光伏发电系统的功率变化过程是一个非平稳的随机过程，既有一定的波动性和随机性，又有一定的周期性。不同季节的太阳入射角、日照时间、光照强弱等存在差异性，到达地面的辐照强度明显不同，光伏系统输出功率的大小会随着辐照强度的变化而变化，这种差异性变化也正是季节类型对光伏发电系统功率影响的具体体现。除了季节类型，天气类型对输出功率的影响也是不容忽视的。图1 是相同天气类型下，某任意两天的输出功率与辐照强度的对应曲线，其中前一天对应的季节类型是夏季，后一天对应的季节类型是冬季，为了增强对比的明显性，对输出功率和辐照强度进行了归一化处理。图2 是同一季节类型下，不同日期的光伏系统的输出功率曲线，对应日期的气象信息如表1 所示。

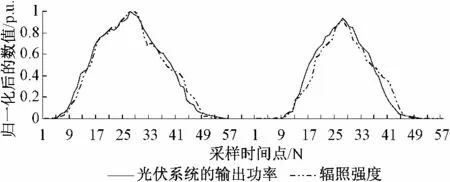
图1 输出功率与辐照强度的对应曲线Fig.1 Corresponding curves of output power and radiation intensity

图2 不同日期的光伏系统的输出功率曲线Fig.2 Output power curve of PV system in different dates

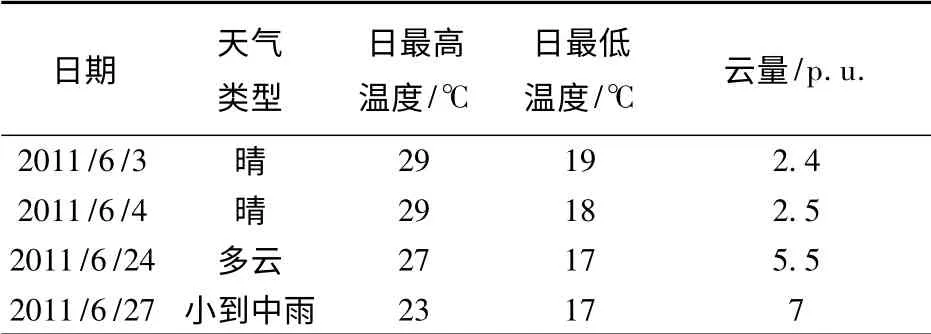
表1 对应日期的气象信息Tab.1 Meteorological information of corresponding date

结合图1、图2 和表1 可知，光伏系统输出功率的变化曲线与辐照强度大致相同，二者之间具有较强的相关性;不同季节或天气类型的输出功率曲线差别很大，这种差异性既体现在曲线变化趋势上，也体现在功率数值大小上;相同季节和天气类型输出功率的变化曲线具有一定的相似性，但随着辐照强度、温度等气象因素的差异性变化，输出功率也呈现一定的差异性变化。

2.2 样本的选取及输入变量的确定

目前我国太阳辐射观测站点较少，较难获得大量的辐照强度数据，且辐照强度会随气象条件的变化而变化，云量作为描述天空遮蔽程度的气象因子，它的增加会导致地面辐照强度的减小，但云量对光伏功率的作用机理比较复杂，本文只简单考虑把云量作为一个影响因子输入模型，云量这一测量数据来自当地气象观测站。大量研究表明辐照强度与光伏功率的变化趋势基本一致，光伏功率的变化趋势可以映射辐照强度的变化趋势［4，9，19］，图1 也很好地体现了输出功率与辐照强度的这一对应关系。本文选取日最高温度、日最低温度和云量作为主气象影响因素，为了提高不同天气类型下的预测精度，采用相似日原理确定样本，具体相似日［20，21］的选取步骤如下:

(1)根据预测日的季节及天气类型初步确定训练样本。

(2)统计初步样本的日最高温度、日最低温度和云量信息，每日的气象特征模式向量为

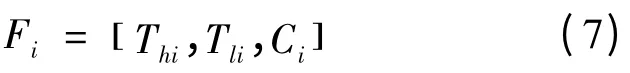
式中:Thi为第i日的日最高温度;Tli为第i日的日最低温度;Ci为第i日的云量。

(3)对气象特征模型向量进行最大最小法归一化处理，并按照灰色关联系数法计算预测日和第i日第k 个气象特征向量的关联系数，计算式如式(8):

式中:ρ 为常数，一般取值为0.5;f0(k)，fi(k)分别为预测日和第i日第k 个气象特征向量的分量。

(4)按式(9)计算整日的关联度ri，选取关联度最大的历史日最为预测日的相似日。

对于既定的光伏电站，光伏阵列安装位置、转换效率等可以看作是隐含在光伏功率数据中的变量，于是确定利用相似日的光伏功率和预测日及相似日的气象信息实现对预测日光伏功率的预测。为了满足电网调度要求，采样时间间隔为15 min，采样时间段为6:00`20:00，1 天共57 个采样时间点。则模型的输入、输出变量如表2 所示。

表2 模型的输入、输出变量Tab.2 Input and output variables of model

2.3 预测模型的结构及训练

为了克服BP 网络训练速度慢、极易陷入局部极值的缺陷，采用混沌搜索的自适应变异粒子群算法优化BP 网络，不仅增强了BP 网络的泛化映射能力和稳定性，也提高了网络的收敛速度和预测精度。预测模型的结构如图3 所示。

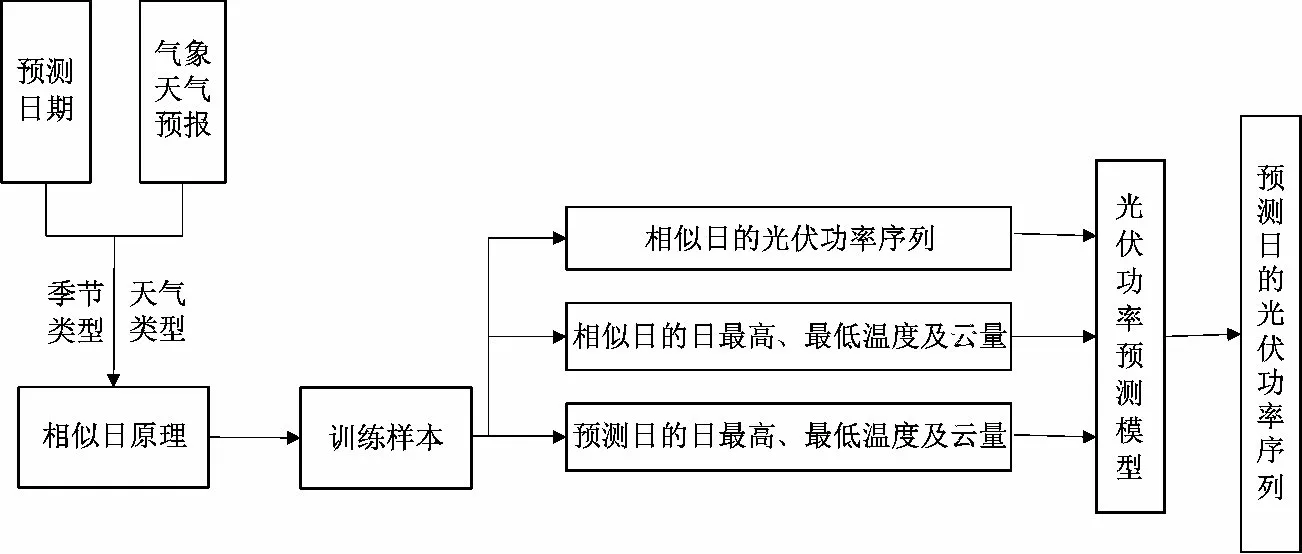
图3 预测模型的结构框图Fig.3 Block diagram of prediction model

基于混沌搜索的AMPSO-BPNN 算法的实质就是将输入、输出问题转化成非线性映射问题，利用混沌搜索的自适应变异粒子群初始化BP 算法的权重阈值，再利用BP 算法进行局部寻优。训练的大致过程如下:

(1)初始化BP 网络的结构，设定其输入、输出和隐层神经元个数及相关参数，其中隐层神经元个数根据误差最小原则确定。

(2)采用混沌优化算法产生一系列初始解，择优选出初始种群初始化种群中各粒子的速度和位置，以提高初始种群的多样性和粒子搜索的遍历性。

(3)根据混沌搜索的自适应变异粒子群算法寻找全局最优解，并初始化BP 网络的权重阈值。

(4)凭借BP 网络较强的逼近能力和局部搜索能力，构建基于混沌搜索的AMPSO-BPNN 的光伏功率预测模型，实现对未来的光伏功率预测。基于混沌搜索的AMPSO-BPNN 的光伏功率预测模型的训练过程如图4 所示。

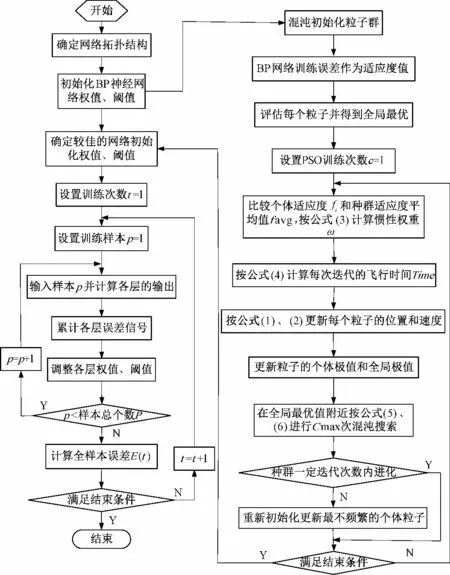
图4 混沌搜索的AMPSO-BPNN 预测模型的训练过程Fig.4 Training process of prediction model based on chaos search and AMPSO-BPNN

3 实例分析

本文选取2011年7月份的连续7 天作为预测日，其中晴天2 天、多云天3 天、阴雨天2 天，采用所提方法进行预测。预测模型采用Microsoft Visual C+ + 6.0 编程实现，以某光伏电站结合气象观测数据为例进行验证，以15 min 为步长，预测上述7 天的6:00 ～20:00 时间段的光伏发电出力。

为了验证所建模型在光伏功率预测中的有效性，采用相同训练样本进行不同模型的分析比较，模型1 为基于BP 算法神经网络的预测模型，模型2 为基于标准PSO 优化BP 神经网络的预测模型，模型3 为基于混沌搜索与AMPSO 优化BP 神经网络的预测模型。预测曲线如图5 所示，a.是模型1 的预测值与实际值的对比曲线，b.是模型2 的预测值与实际值的对比曲线，c.是模型3 的预测值与实际值的对比曲线;对应的相对误差曲线如图6 所示，a.是模型1 的相对误差曲线，b.是模型2 的相对误差曲线，c.是模型3 的相对误差曲线。

结合图5 和图6 可知:3 种模型基本都能预测光伏功率的变化趋势;多云天和雨天等复杂天气的相对误差明显大于晴天，即多云天和雨天的预测效果远不如晴天;预测误差较大的时刻多发生在早晚时间段，原因在于此时间段水汽凝结产生轻雾、城市污染等比较严重，使得大气透明度降低，辐照强度较小，气象因素对光伏功率的影响机理更为复杂。

图5 模型的预测曲线Fig.5 Prediction curve of model

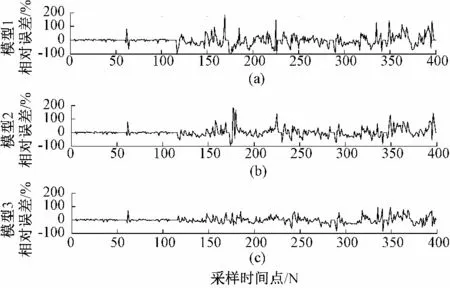
图6 模型的相对误差曲线Fig.6 Relative error curve of model

考虑到夜间时段的光伏出力为零，本文采用改进的平均绝对百分比误差(IMAPE)及均方根误差(RMSE)评价模型的整体性能，计算公式如式(10)、(11)所示。公式(10)的定义方法将误差限定在［0，1］范围内，避免了当实际值为零而预测值不为零时相对误差无限大的情况。此处，当实际值和预测值均为零时，不存在预测误差，即认为相对误差为零。3 种模型的预测误差结果如表3 所示。

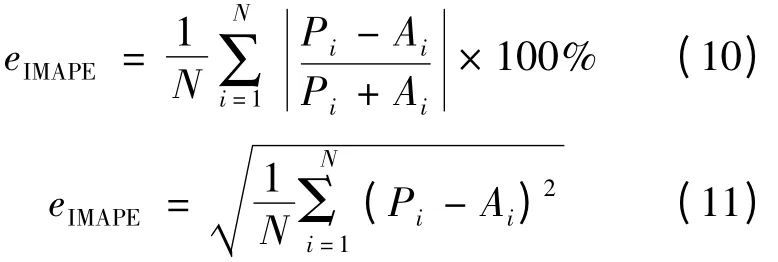
式中:Pi为第i 时刻光伏发电功率实际值;Ai为第i时刻光伏发电功率预测值。

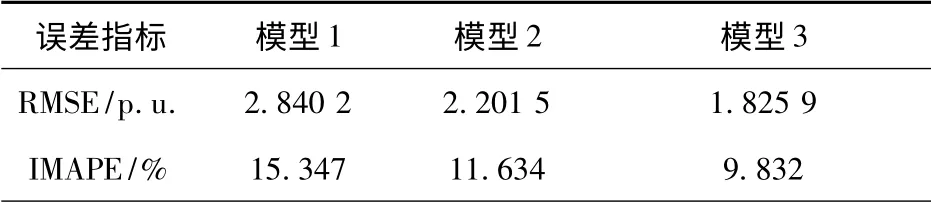
表3 模型的预测误差Tab.3 Prediction error of model

从表2 可以看出，经混沌搜索的自适应粒子群优化后模型的RMSE 由2.840 2 降为1.825 9，IMAPE 由15.347 %降为9.832 %，无论是均方根误差，还是改进平均绝对百分比误差，模型3 的预测误差最小，模型2 次之，模型1 最大。可见，基于混沌搜索的AMPSO-BP 神经网络算法能较好地改善传统BP 算法和PSO 算法的缺陷，提高算法的预测精度和收敛速度，有力地验证了所提模型及算法在光伏功率预测中的有效性。

4 结 论

针对光伏发电系统输出功率的随机性和波动性，建立了基于混沌搜索的AMPSO-BPNN 的光伏功率预测模型。利用混沌搜索的自适应变异粒子群算法初始化BP 网络的权重阈值，既能提高算法的广度搜索能力，又能提高其深度搜索能力，保证了BP 网络的稳定性;在建模过程中充分考虑季节、天气类型及辐照强度、温度和云量等气象因素的影响，有效地提高模型在不同天气类型下的预测精度;最后利用实例数据进行模型计算分析，预测结果满足工程应用需求，同时验证了所提模型和算法在光伏功率预测中的可行性。

［1］陈炜，艾欣，吴涛，等.光伏并网发电系统对电网的影响研究综述［J］.电力自动化设备，2013，33(2):26 －32.

［2］王飞，米增强，杨奇逊，等.基于神经网络与关联数据的光伏电站发电功率预测方法［J］.太阳能学报，2012，33 (7):1171 －1177.

［3］M Riley D，K Venayagamoorthy G.Characterization and modeling of a grid-connected photovoltaic system using a recurrent neural network ［C］.2011 International Joint Conference on Neural Network (IJCNN)，San Jose，CA，USA，2011.1761 －1766.

［4］王守相，张娜.基于灰色神经网络组合模型的光伏短期出力预测［J］.电力系统自动化，2012，36(19):37 －41.

［5］王哲，王飞，刘力卿，等.基于多元回归分析的光伏电站太阳辐射曝辐量模型［J］.华北电力大学学报，2011，38 (5):53 －58.

［6］曹双华，曹家枞.太阳逐时总辐射混沌优化神经网路预测模型研究［J］.太阳能学报，2006，27 (2):164 －169.

［7］T Shimada，K Kurokawa.Grid-connected photovoltaic systems with battery storages control based on insolation forecasting using weather forecast ［J］.Renewable Energy，2006:228 －230.

［8］栗然，李广敏.基于支持向量机回归的光伏发电出力预测［J］.中国电力，2008，41 (2):74 －78.

［9］朱永强，田军.最小二乘支持向量机在光伏功率预测中的应用［J］.电网技术，2011，35 (7):54 －59.

［10］张佳伟，张自嘉.基于PSO-BP 神经网络的短期光伏系统发电预测［J］.可再生能源，2012，30 (8):28－32.

［11］王晓霞，王涛，谷根代.基于改进粒子群优化的神经网络及应用［J］.华北电力大学大学学报，2009，36 (5):99 －102.

［12］王贺，胡志坚，张翌晖，等.基于IPSO-LSSVM 的风电功率短期预测研究［J］.电力系统保护与控制，2012，40 (24):107 －112.

［13］陈刚，简华阳，龚啸.自适应混沌粒子群算法在PSS设计中的应用［J］.电力系统及其自动化学报，2012，24 (4):82 －87.

［14］H Siahk ali，M Vak ilian.Electricity generation scheduling with large-scale wind farms using particle swarm optimization ［J］.Electric Power System Research，2009，79 (5):826 －836

［15］周孝法，陈陈，杨帆，等.基于自适应混沌粒子群优化算法的多馈入直流输电系统优化协调直流调制［J］.电工技术学报，2009，24 (4):192 －201.

［16］董勇，郭海敏.基于群体适应度方差的自适应混沌粒子群算法［J］.计算机应用研究，2011，28 (3):854 －856.

［17］邓爱萍，王会芳.动态改变惯性权重的自适应粒子群算法［J］.计算机工程与设计，2010，31 (13):3062 －3065.

［18］易文周，田立伟.一种基于混沌搜索和鲶鱼效应策略的粒子群算法［J］.计算机应用与软件，2013，30 (5):311 －315.

［19］张艳霞，赵杰.基于反馈型神经网络的光伏系统发电功率预测［J］.电力系统保护与控制，2011，39(15):96 －101.

［20］王晓兰，葛鹏江.基于相似日和径向基函数神经网络的光伏阵列输出功率预测［J］.电力自动化设备，2013，33 (1):100 －103.

［21］傅美平，马红伟，毛建容.基于相似日和最小二乘支持向量机的光伏发电短期预测［J］.电力系统保护与控制，2012，40 (16):65 －69.