对中国产业资本劳动替代弹性的估计

范晓静

（上海理工大学 管 理学院，上海 2 00093）

0 引言

在CGE模型的均衡分析中，相比较超越对数、Leontief函数、标准二次函数，CES函数更适合于CGE模型的均衡分析（Perroni等，1998）。但相对于其他函数形式，CGE模型的模拟结果对CES函数参数的取值也更为敏感（Mckitrick et al，1998），因此，采用适合的、科学的方法对模型中产业部门的弹性值的确定是非常重要的。

CES函数是常替代弹性生产函数的简称，其标准格式为：

其中，q为产出，xi为投入的要素，参数A为转移参数，衡量要素投入转化为最终产出的效率，因此也称为全要素生产率。δi为第i种要素的份额，有参数ρ与替代弹性相关，其与替代弹性的关系为替代弹性就是指一个生产系统中，不同生产要素替代的难易程度，替代弹性越大，要素之间越容易替代，反之，越不容易替代。

可以看到，在CES函数的三个主要参数——转移参数、份额参数以及替代弹性中，替代弹性是最为关键的参数，这一方面是因为转移参数、份额参数在一定程度上由替代弹性决定，另一方面则是因为替代弹性反映了CES函数的经济意义，决定了不同投入要素之间的相对地位关系。尽管替代弹性如此重要，但替代弹性的获得却较其他两个参数更为复杂。替代弹性值的确定需要依据以往数据，采用计量方法获得。在数据缺失的情况下，研究者们也常依靠相关文献资料确定替代弹性的采用值。本文对CES生产函数中的要素替代弹性进行估计。

CES函数弹性估计通常采用两种方法进行估计实验，然后依据经济背景确定最终值。这两种方法是贝叶斯（Bayesian）方法和广义最大熵（Generalized Maximum Entropy，GME）方法。简便起见，本文在计算CES生产函数弹性值时只考虑资本和劳动力两要素数据进行估计。

1 广义最大熵（GME）方法对资本劳动替代弹性的估计

在信息论中，随机变量的不确定性可以用熵来衡量。当系统处于不同状态，每种状态出现的概率为Pi(i=1，2，…，n)，那么该系统的熵的定义就为：

Jaynes（1957）提出了最大熵（Maximum Entropy，ME）原则，其基本思想是：在非适定问题的所有解中，应选取符合约束条件，但熵值最大的一个。这是唯一正确选择，任何其他选择都意味着对未知信息做了随意假设。广义最大熵（Generalized Maximum Entropy，GME）是对ME原理的扩展，由Golan等（1996）提出。一般认为，ME原则是针对系统内的一个随机变量的，而GME则是同时最大化系统内所有随机变量的信息熵，也所谓“广义”的含义。GME除了利用已知信息外，不对任何未知信息做先验假设，在其框架内，参数估计转换为有约束的最优化问题，目标函数是最大化未知参数和误差项的联合熵（Golan等，1999）。

GME的基本思想是把所有未知参数变换为概率形式：首先把未知参数和误差重新参数化为离散型随机变量的凸组合，然后用新参数重写模型作为一致性约束条件，然后构造GME目标函数，结合正则化约束条件和一致性约束条件后，进行数值求解，参数的GME解是一致性约束的拉格朗日乘子、参数的支持空间和样本数据的函数（Zhang等，2001）。其优点是在小样本情况下，GME对未知参数和误差性同时估计比只估计参数更有效。

在运用GME方法对CES函数进行估计时，需要首先对资本和劳动力通过CES函数形式结合而成的生产函数（等式(1)）：

通过对其两边取对数进行线性化，在ρ=0处进行泰勒级数展开，取二阶线性部分，并舍去二阶以上高阶项，得到CES函数的线性近似表达为：

其中，β0=lnA，β1=δ，β2=1-δ，β3=-0.5ρδ(1-δ)。这样就可以利用GME方法对其进行估计了。本文利用SAS软件中的GME估计模块进行估计，数据来源于中国统计年鉴各年产业数据。模拟结果如表1所示。

2 贝叶斯方法对资本劳动替代弹性的估计

贝叶斯定理的文字描述如下：

联合后验概率密度∝先验概率密度×似然函数

其中，∝表示成比例。从该式中可以看到，先验概率密度描述了所有先验信息，而有关样本的所有信息则通过似然函数表达。因此，得到的后验概率密度集中了总体、样本和先验中有关参数的一切信息，同时又排除了一切与参数无关的信息（茆诗松，1999；泽尔纳，2005）。在获得相关参数的先验信息后，就可以通过贝叶斯方法估计CES函数中资本劳动替代弹性。此外，该方法可以较容易地扩展到两个以上投入要素的参数估计中，也可以用了估计嵌套的CES函数（泽尔纳，1971；Tsurumi et al，1976；Mckibbin et al，1999）。本文以Lancaster（2004）的方法进行贝叶斯估计。在两要素CES函数中：

对上式两边取对数，引入误差项ε，并假设K、L为外生变量且独立于ε，得到：

其中，q=lnQ，k=lnK，l=lnL，α=lnA。假设误差项ε服从均值为零、方差为τ的正态分布，记参数向量θ=(α,β,δ,τ)。则似然函数为：

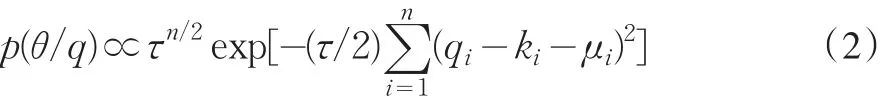
对于先验信息的概率密度

p(θ)=p(α,β,δ,τ)，假设α服从正态先验分布，τ服从Gammar先验分布；由于δ的取值范围在0和1之间，假设其在该区间上服从均匀分布作为其先验分布；对于ρ，根据σ=1/(1+ρ)，根据郑玉歆等（1999）年计算的中国不同部门的生产弹性值的大致范围在0.1和2之间，故取对应的（-0.5，9）区间上的均匀分布作为其先验分布（赵永，王劲松，2008）。这样，在给定Q、K、L观测数据的基础上，就可以得到参数向量的联合后验概率密度：

对此式进行积分，就可以得到参数的后验密度。通过对等式（2）中的τ进行积分，可以得到参数α,β,δ的联合后验密度；继续对α进行积分，可以得到β,δ的联合后验密度。

本文运用WinBUGS软件利用我国统计年鉴中各产业历年的数据值，对上CES生产函数参数进行估计，代码可参见赵永，王劲松（2008），得到的各产业部门资本劳动替代弹性值如表1所示，其后验分布核密度和收敛性诊断图如图1至图16所示。

图1-1 采掘业σ后验分布核密度

图2-1 农业σ后验分布核密度

图1-2 采掘业σ收敛性诊断图

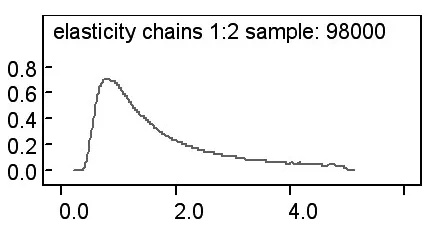
图3-1 制造业σ后验分布核密度

图2-2 农业σ收敛性诊断图

图4-1 电热水业σ后验分布核密度

图3-2 制造业σ收敛性诊断图

图5-1 建筑业σ后验分布核密度

图4-2 电热水业σ收敛性诊断图

图5-2 建筑业σ收敛性诊断图

图6-1 交通运输业σ后验分布核密度

图7-1 软件通信业σ后验分布核密度

图6-2 交通运输业σ收敛性诊断图

图7-2 软件通信业σ收敛性诊断图

图8-1 零售餐饮业σ后验分布核密度

图8-2 零售餐饮业σ收敛性诊断图

图9-1 金融业σ后验分布核密度

图10-1 房地产业σ后验分布核密度

图9-2 金融业σ收敛性诊断图

图10-2 房地产业σ收敛性诊断图

图11-1 租赁业σ后验分布核密度

图11-2 租赁业σ收敛性诊断图

图12-2 社会服务业σ收敛性诊断图

图12-1 社会服务业σ后验分布核密度

图13-1 教育业σ后验分布核密度

图13-2 教育业σ收敛性诊断图

图14-1 卫生服务业σ后验分布核密度

图14-2 卫生服务业σ收敛性诊断图

图15-1 文化娱乐业σ后验分布核密度

图15-2 文化娱乐业σ收敛性诊断图

图16-2 公共管理业σ收敛性诊断图

3 模拟结果比较

从表1对CES生产函数劳动与资本的替代弹性进行估计的结果来看：

表1 Bayesian方法和GME方法估计的弹性值的统计结果

农业：两种方法估计的σ值相差不大，同时收敛性统计图也表明弹性值趋于收敛，且稳定。但是GME方法估计出的σ值与相关文献更为接近，因此，农业部门的σ值采用GME方法的估计结果。

采掘业：贝叶斯方法计算出的σ值为负值，故采用GME方法的估计结果。

制造业：两种方法得到的σ值相差不大，但GME方法得到的标准差比贝叶斯方法得到的要大很多，贝叶斯方法的收敛性诊断图显示σ参数的收敛性很好，因此，制造业部门的σ值采用贝叶斯方法的估计结果。

水电热业：两种方法得到的σ值的统计数据均较理想，但贝叶斯方法的收敛性诊断图显示σ参数的收敛性很好，同时更接近于相关文献的数据，因此，选择贝叶斯方法的估计结果作为水电热业的估计值。

建筑业：两种方法得到的σ值较为接近，但从贝叶斯方法的收敛性诊断图可以看到建筑业的σ参数的收敛性并不好，因此，选择GME方法估计的结果作为建筑业的σ参数值。

交通仓储业：两种方法得到的σ值较为接近，但贝叶斯收敛性诊断图显示σ参数开始时收敛性较好，但后期收敛性并不好，因此，交通仓储业的σ参数值采用GME方法的估计结果。

通信软件业：贝叶斯方法得到的σ参数值为负数，GME方法得到的σ参数各项指标较满意，因此，通信软件业的σ参数值采用GME方法估计的结果。

批发零售业：两种方法得到的σ参数值的统计数据均较理想，但从贝叶斯方法的收敛性诊断图可以看到，σ参数的收敛性可以接受，但到后期并不稳定，因此，选择GME方法估计的结果作为批发零售业的σ值。

金融业：两种方法得到的σ参数值相差较大，但两种方法的各项统计指标都比较理想，σ参数的估计值的收敛性也很好且稳定。参考相关文献，贝叶斯方法估计的参数值偏小，GME方法得到的结果更为理想，因此采用GME方法估计的结果。

房地产业：两种方法估计的结果很接近且各项统计值也比较理想，但贝叶斯方法得到的收敛性诊断图显示σ参数的收敛性较好但并不稳定，因此，采用贝叶斯方法作为房地产业的σ参数值。

租赁服务业：两种方法估计的结果较为接近，但贝叶斯方法得到的收敛性诊断图显示σ参数的收敛性并不稳定，因此，采用GME方法估计的结果。

社会服务业：两种方法估计的结果相差较大，从相关的统计项来看，贝叶斯方法中得到的σ参数的标准差过大，并且收敛性诊断图显示其收敛性也并稳定，因此，采用GME方法估计的结果作为σ的参数值。

教育业：贝叶斯方法得到的σ参数值为负数，并且从收敛性统计图来看，该值也并不收敛，因此，教育业的σ值采用GME方法的估计结果。

卫生：从收敛性统计图来看，卫生与社会保障业的σ参数值收敛且稳定，但其估计得到的σ参数值为负数，因此，采用GME方法估计的结果作为σ参数值。

文化娱乐业：两种方法得到的σ参数值很接近，但从收敛性统计图来看，文化娱乐业的σ参数值收敛性欠佳，因此，采用GME方法的估计结果。

社会管理：采用贝叶斯方法估计的社会管理业的σ值为负数，并且从收敛性统计图来看，该行业的σ参数值也并不收敛，而GME方法估计的结果各项统计值较好，因此，采用GME方法估计的结果作为σ参数值。

综合以上分析，得到的各个产业部门的CES生产函数资本劳动的替代弹性值如表2所示。

4 结论

本文利用贝叶斯方法和广义最大熵方法对常替代生产函数中的资本劳动替代弹性值进行了估计，通过比较确定了我国16个产业部门的资本劳动替代弹性。本文的估计结果对利用常替代弹性函数刻画我国产业部门的生产具有参考意义。而对嵌套的资本劳动替代弹性的估计则是未来的研究方向。

表2 各产业的CES生产函数资本劳动替代弹性值

[1]赵永,王劲峰.经济分析CGE模型与应用[M].北京:中国经济出版社,2008.

[2]张欣.可计算一般均衡模型的基本原理与编程[M].上海：格致出版社，2010.

[3]茆诗松.贝叶斯统计[M].北京：中国统计出版社，1999.

[4]泽尔纳著，张尧庭译.计量经济学贝叶斯推理引论[M].上海：上海财经大学出版社，2005.

[5]郑玉歆,樊明太.中国CGE模型及政策分析[M].北京:社会科学文献出版社,1999.

[6]McKitrick,Ross R.The Econometric Critique of Computable General Equilibrium Modeling:The Role of Functional Forms[J].Economic Modeling,1998,（15）.

[7]Prroni C.,T.F.Rutherford.A Comparison of the Performance of Flexi⁃ble Functional Forms for LES in Applied General Equilibrium Model⁃ling[J].Computational Economices,1998,(11).

[8]Jaynes E.T.Information Theory and Statistical Mechanics[J].Physical review,1957,106(4).

[9]Golan A.,G.Judge,D.Miller.Maximum Entropy Econometrics:Robust Estimation with Limited Data[M].Chiehester,England:John Wiley&Sons Ltd,1996.

[10]Golan A.,E Moretti,J.M.Perloff.An Information-Based Sample-Se⁃lection Estimation Model of Agricultural Workers’Choice between Piece-Rate and Hourly Work[J].American Journal of Agricultural Economics,1999,81(3).

[11]Zhang X.,S.Fan.Estimation Crop-Specific Production Technologies in Chinese Agriculture:A generalized Maximum Entropy Approach[J].American Journal of Agricultural Economics,2001,83(2).

[12]Tsurumi H.A Bayesian Estimation of Macro and Micro CES Produc⁃tion Fuctions[J].Journal of Econometrics，1976,4(1).

[13]Mckibbin W.J.,R.Shackleton.,P.J.Wilcoxen.What to Expect from an International System of Tradable Permits for Carbon Emissions[J].Resource and Energy Economics,1999,(21).

[14]Lancaster T.An Introduction to Modern Bayesian Econometrics[M].Cambridge Blackwell Publishing Ltd,2004.