共轴载流正三角形线圈间的相互作用

呼格吉乐 王桂斌 邱为钢

（湖州师范学院理学院，浙江 湖州 313000）

载流线圈间电磁相互作用的研究是电磁学中的常见问题.常见的模型是平行共轴相似的两个载流线圈，理论上讨论线圈之间的作用力与距离的关系［1，2］.对于圆形线圈来说，绕轴线转动任意角度，对于系统作用量（互感产生的磁能）没有任何影响，不需要克服力矩来恢复到原有位形，这意味着共轴平行圆形线圈之间是没有力矩的.对于矩形线圈，文献［3］提出把互感磁能当作系统的作用量.这个作用量与线圈的距离有关，对距离的偏导数就是两个线圈的相互作用力.文献［3］忽略了更一般的情况，即两个矩形线圈有交错角度，这样系统作用量不仅与距离有关，也与角度有关.系统作用量对于角度的偏导数，就是两个线圈的力矩.为简单起见，我们以共轴平行正三角形线圈为例，研究线圈之间相互作用力和力矩与线圈距离，交错角度的关系.交错角度载流正三角型线圈存在力矩这个理论预言，也得到文献［4，5］上的实验验证.

1 三角形载流线圈互感系数的坐标表示

稳恒线段电流元在空间任意一点产生的磁感应强度由毕奥-萨伐尔定律给出，由此可以得到线段电流元在一个三角形上的磁通量的表达式，虽然这个表达式不一定有解析表示，但对于数学软件（如Mathematica）来说，只要给出表达式，就可以数值求值.所以先给出线段电流元通过三角形磁通量的坐标表达式.

设（i，j，k）是通常三维直角坐标系中的正交单位矢量，考虑起点在r1＝x1i＋y1j＋z1k，终点在r2＝x2i＋y2j＋z2k稳恒线段电流元在场点r＝xi＋yj＋zk所产生磁感应强度的表达式，电流线段上任意一点的参数表达式是

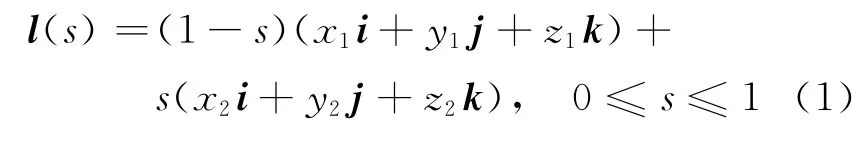
由此得到电流元的表达式是

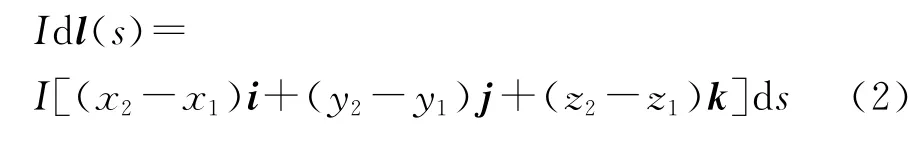
场点到电流元的位移是

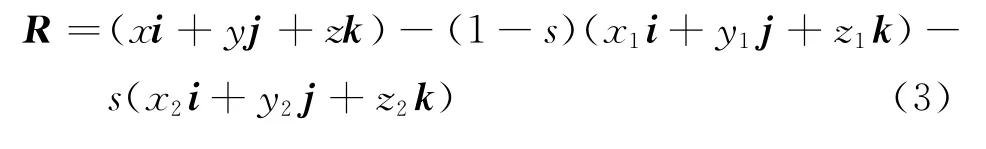
电流元在场点产生的磁感应强度是

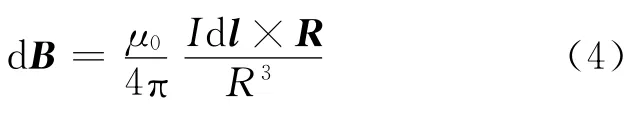
由式（2），（3），（4），得到磁感应强度的第三分量是

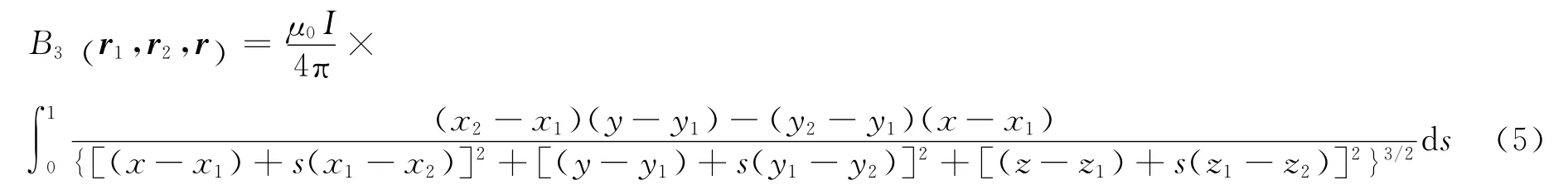
设场点r＝xi＋yj＋zk在三角形内部，三角形三个顶点坐标分别为zk，r3＝x3i＋y3j＋zk，r4＝x4i＋y4j＋zk.那么（x，y）的两参数表示为

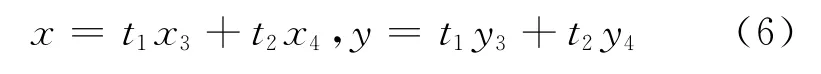
其中，参数 （t1，t2）满足0≤t1＋t2≤1.设三角形的面积为A，三角形的面元为dA＝2Adt1dt2.由（4），（5），（6）三式，得到互感系数的坐标表达式是

2 共轴正三角形载流线圈的相互作用力

设两个共轴平行的正三角形载流线圈ABC和A′B′C′，分别通以电流Ⅰ，Ⅰ′，线圈中心相距z.顶点坐标分别为

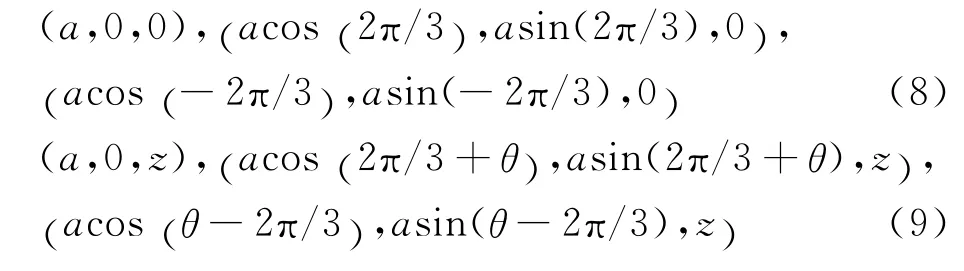
把上面的三角形A′B′C′分成三个以轴线为顶点的小三角形，然后利用式（7），（8），（9），形式上（可以方便编程数值计算，具体细节请参考文献［4］）得到互感系数的表示

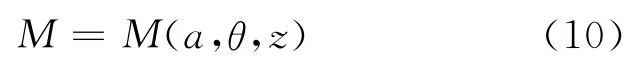
由此得到共轴平行正三角形载流线圈的相互作用力为

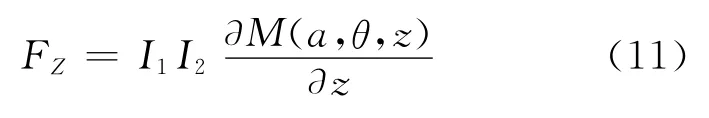
当两个正三角形线圈没有交错角度时，相互作用力与线圈中心距离z的关系曲线如图1所示.

当两个正三角形线圈存在不同的交错角度时，相互作用力与线圈中心距离z的关系曲线如图2，3所示.

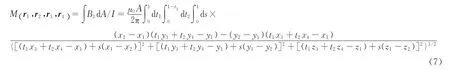
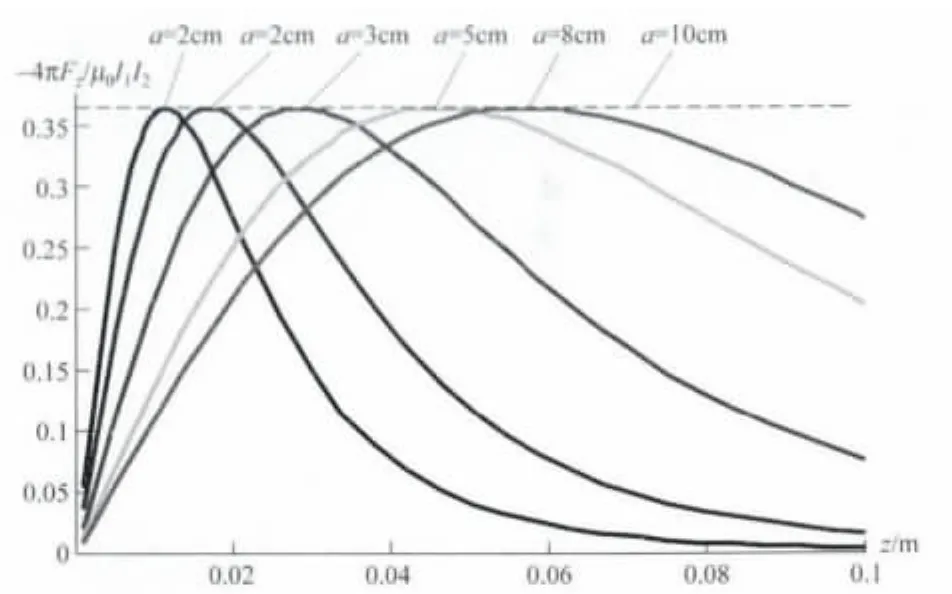
图1 对称正三角形载流线圈相互作用力与距离的关系

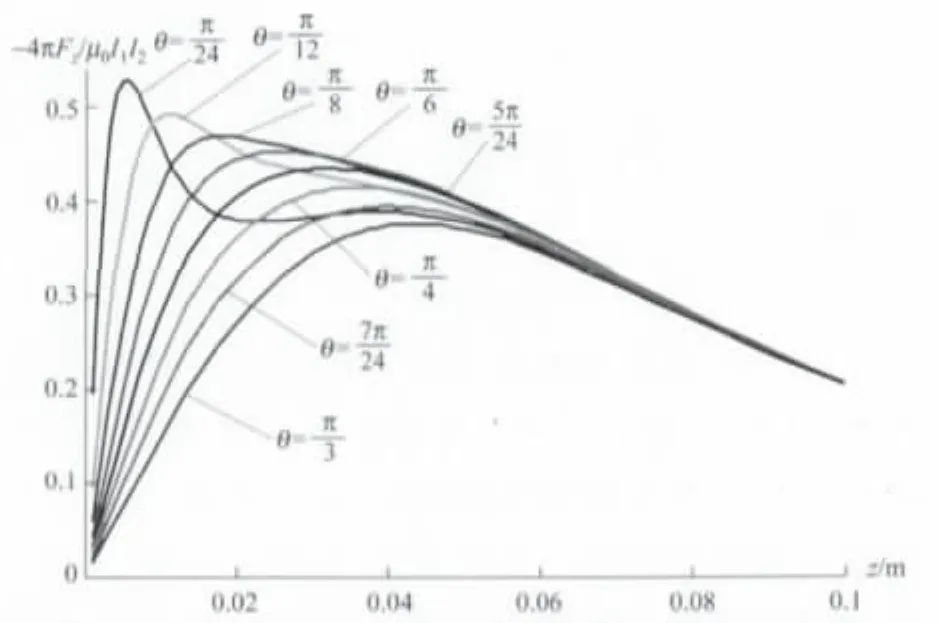
图2 正三角形载流线圈相互作用力与距离的关系

数值计算发现，当两个正三角型线圈角度较小或较大时，线圈的相互作用力随线圈距离变化，有极大和极小值，这与对称情况下只有一个极大值有明显不同.当线圈距离很大时，线圈可以看作两个磁偶极距（只与线圈的面积有关），这时候，交错不同角度线圈的相互作用力就趋向于同一个极限值.

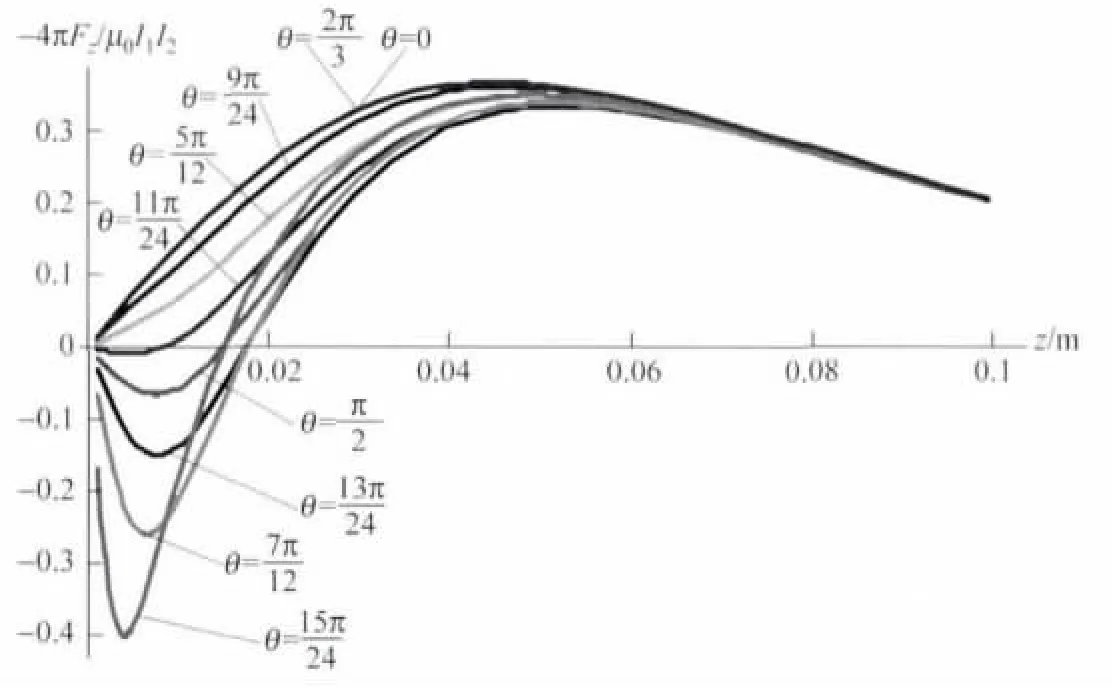
图3 正三角形载流线圈相互作用力与距离的关系

3 共轴正三角形载流线圈间的力矩

根据虚位移原理，共轴正三角形载流线圈间的电磁力矩为

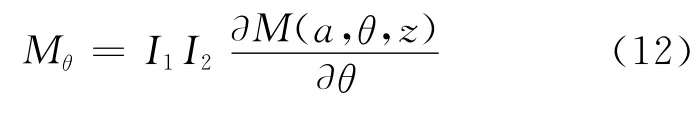
当两个正三角形线圈存在交错角度时，力矩与交错角度θ的关系曲线如图4所示

由图4可以发现，虽然两个正三角形线圈间距离不同，但力矩Mθ随θ是周期变化的，且周期都是2π／3.力矩的极大值出现在θ＝0位置，即对称位置；力矩的极小值出现在θ＝π／3位置，即反对称位置.

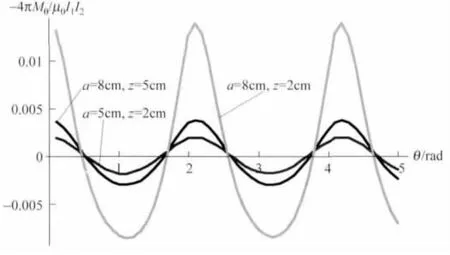
图4 正三角形载流线圈力矩和线圈间转角的关系

4 结论

对于共轴正三角形载流线圈间相互作用力和力矩，均作了数值计算.通过绘制关系曲线，两共轴对称正三角形载流线圈间的相互作用力与圆形线圈［2］或矩形线圈［3］间的相互作用力规律基本一致.但是，当相对转角取得某一值时，曲线出现了正负两个极值.我们还研究了共轴载流线圈间的力矩，得到力矩随线圈转角的变化周期不随线圈间距离变化，固定为2π／3角度.

［1］张伟，陈俊斌.同轴等大线圈互感系数及相互作用力的近似解析公式［J］.大学物理，2004，23（8）：36-40.

［2］朱思华，杨万民.两共轴平行圆环电流之间的电磁作用力［J］.大学物理，2005，24（10）：24-26.

［3］王树平，崔红娜，范虹，等.共轴载流矩形线圈间的相互作用力［J］.物理与工程，2007，17（5）：12-16.

［4］王桂斌.三角形线圈间的相互作用［D］.湖州师范学院2010届毕业论文.

［5］呼格吉乐，邱为钢.三角形旋转跳环［J］.大学物理实验，2012，25（6）：57-58.