核磁共振实验和铁磁共振实验的搭建思想分析

邱正明 杨 旭 梁 燕

（中国科学技术大学物理实验教学中心 ，安徽 合肥 230026）

由于磁共振能反映物质结构和物质内部的动态信息又不破坏物质结构本身，而且具有较高的灵敏度和分辨本领，因而在物理、化学、生物、医学、计量等领域得到了广泛的应用.

核磁共振实验和铁磁共振实验是本科大学物理实验的基本实验，但是有些大学在物理实验过程中大多忽略实验的设计性，学生往往只对数据进行测量和分析，多是验证性试验，而忽略实验系统的组成和搭建，而恰恰实验的搭建思想才是实验的精华，它是理论和工程知识相结合的产物，是培养学生理论与实践相结合的重要环节.

本文介绍核磁共振实验和铁磁共振实验的搭建思想.

1 核磁共振的基本原理

自旋不为零的粒子，如电子和质子，具有自旋磁矩.如果把这样的粒子放入稳恒的外磁场中，粒子的磁矩就会和外磁场相互作用使粒子的能级产生分裂，分裂后两能级间的能量差为

其中：γ为粒子的旋磁比，为约化普朗克常数，B0为稳恒外磁场的磁感应强度.

如果此时再在稳恒外磁场的垂直方向给粒子加上一个高频电磁场，该电磁场的频率为ν，能量为

当该能量等于粒子分裂后两能级间的能量差ΔE时即

则低能级上的粒子就要吸收高频电磁场的能量产生跃迁，即所谓的核磁共振.

2 核磁共振实验搭建思想和装置

由公式（3）可知，为了实现核磁共振有两种实验方法：

1）固定外磁场B0，调节高频电磁场频率ν，实现核磁共振，此为扫频法.

2）固定高频电磁场频率ν，调节外磁场B0，实现核磁共振，此为扫场法.

本实验用的是第二种实验方法，即扫场法.核磁共振实验装置如图1所示.

（1）样品（sample）水：提供实验用的粒子，氢（1H）核.

（2）永磁铁：提供稳恒外磁场，中心磁感应强度B0约为0.55T.

（3）边限振荡器：产生射频场，提供一个垂直于稳恒外磁场的高频电磁场，频率νHz.

（4）边限振荡器同时也具有放大器的作用，将探测到的共振电信号放大后输出到示波器，边限振荡器的频率由频率计读出.

（5）绕在永磁铁外的磁感应线圈：其提供一个叠加在永磁铁上的扫场.

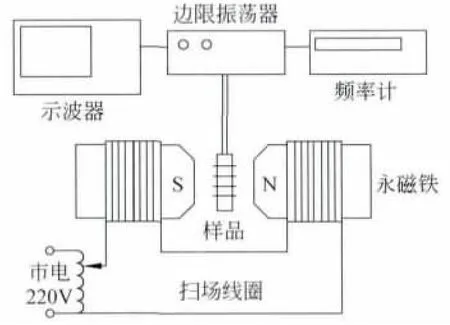
图1 核磁共振实验装置示意图

（6）调压变压器：为磁感应线圈提供50Hz的扫场电压.

（7）频率计：读取射频场的频率.

（8）示波器：观察共振信号.

3 核磁共振实验的搭建

本实验要测的一个物理量是氢质子的γ因子，由公式（3）可知，只要知道B0、ν即可求得γ，B0在实验设备中已标定（如0.55T），ν可由频率计测出.

由公式（3）搭建实验时仅需用磁铁、射频振荡电路、频率计即可完成该实验的搭建，其中样品水作为振荡电路中电感线圈中的介质，绕在线圈中，这样可使线圈中的高频电磁场加在氢质子上.

但是仅此，在本实验中γ是无法用实验求出的.因为本实验中两能级的能量差ΔE＝γB0是一个精确稳定的量.而实验用的高频振荡器的频率ν只能稳定在103Hz量级.其能量hν很难固定在γB0这一值上.实际上等式（3）在实验中很难成立.

为实现核磁共振，改进搭建，在永磁铁上绕一线圈，经由调压变压器通以50Hz的市电，使永磁铁B0上叠加一个低频交变磁场Bmsinωt，即所谓的扫场（ω为市电频率50Hz，远低于高频场的频率ν其约几十 MHz），使氢质子两能级能量差γ（B0＋Bmsin100πt）有一个连续变化的范围.调节射频场的频率ν，使射频场的能量hν进入这个范围，这样在某一时刻等式

总能成立，见图2.

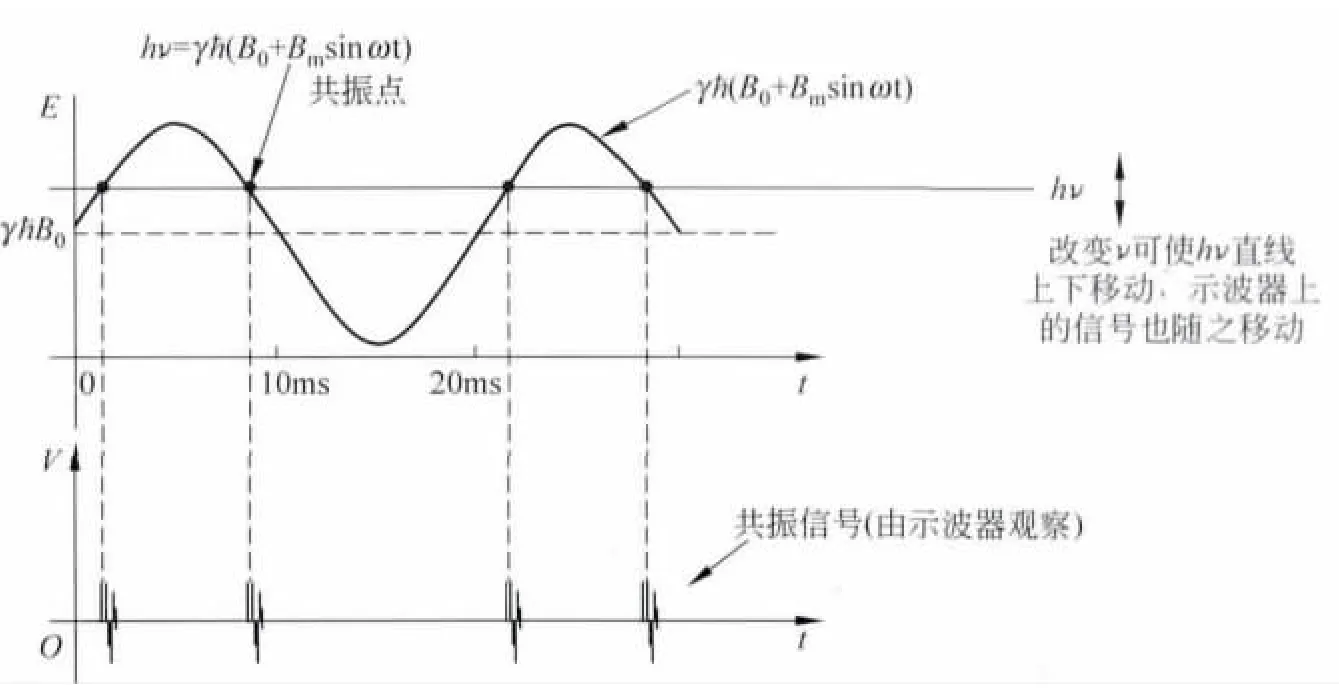
图2 核磁共振函数曲线及其示波器共振信号示意图

此时通过边限振荡器的探测装置在示波器上可观测到共振信号（见图2）.

调节射频场的频率ν使共振信号等间距，共振点处的相角，代入等式得：此时的ν为共振信号等间距时的频率，由频率计读出值可求（见图3）.

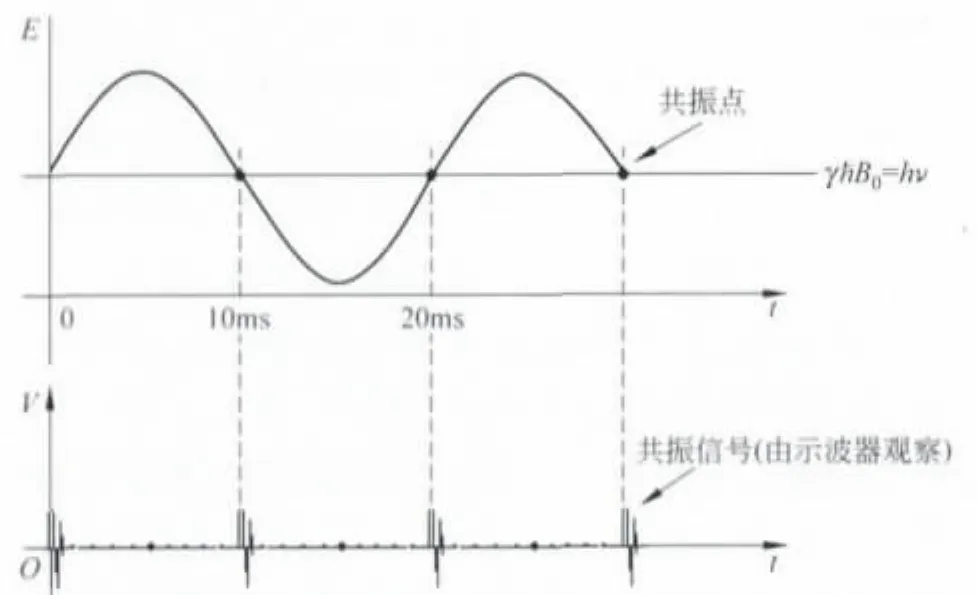
图3 示波器上共振信号等间距时对应的函数关系图

4 探测装置的工作原理

实验中实际边限振荡器的电路简图如图4所示，它是一个等幅震荡的LC并联电路.

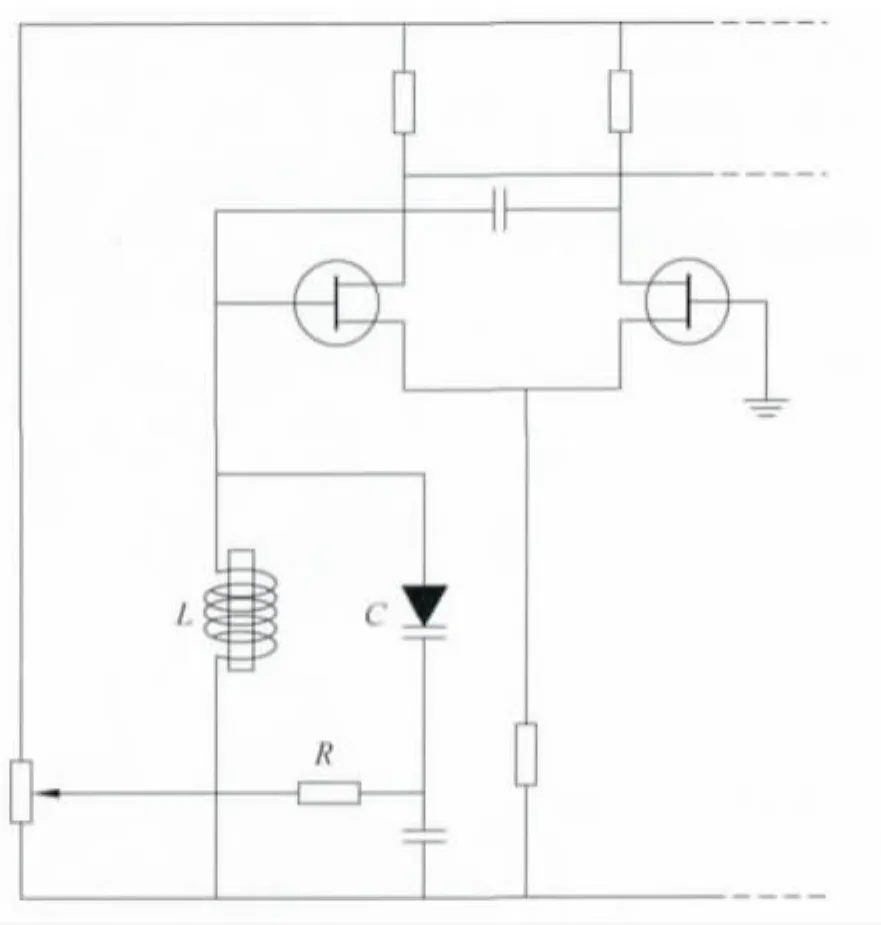
图4 边限震荡器中LC并联振荡电路简图

图4中绕在样品上的线圈是边限震荡器电路的一部分，在非磁共振状态下电路处在边限震荡状态（即似振非振的状态），线圈把电磁能加在样品上，方向与外磁场垂直.当磁共振发生时，样品中的粒子吸收了震荡电路提供的电磁能使振荡电路的发生变化，使振荡电路产生显著的振荡，在示波器上产生共振信号.

如果对振荡电路的Q值的变化作进一步讨论，可从磁共振经典力学的观点加以研究（见图5（a））.

具有磁矩μ和角动量的粒子在稳恒外磁场B0中受到一个力矩作用，粒子磁矩μ绕外磁场B0进动，如在外磁场B0的垂直方向加一旋转磁场B1，其旋转频率与粒子磁矩μ进动频率一致为ω0，则旋转磁场相对于磁矩μ也为一恒定磁场B1，磁矩也要绕旋转磁场B1进动，结果使磁矩μ与稳恒外磁场B0的夹角变大θ1＞θ0（见图5（b））.粒子的磁矩方向发生了变化，沿旋转磁场B1的磁矩加强，增加了电感量，使Q值增加选频特性加强，沿外磁场B0的磁矩减小，由于方向垂直对电感无影响.

图5

在振荡电路中，载有粒子的样品作为介质处于振荡电路的线圈中，与线圈一起组成振荡电路的电感，共振时介质的磁矩发生变化，振荡电路的电感也发生变化，振荡电路的Q值随之变化（电路的选频特性发生变化）.以介质共振吸收时的电感设计电路，使它作为电路的起振电感，则电路在共振吸收发生时将显著振荡，探测到振荡电路的振荡信号，就可间接判断粒子共振吸收的产生.

只有样品的磁矩发生变化，电路才会显著振荡.如果撤去稳恒的外磁场，样品失去共振条件，使得振荡电路的电感不变化，则无论怎样调节振荡电路的电位器来改变电路的可变电容，都不会使电路振荡.

同样维持稳恒的外磁场，撤去样品，调节振荡电路的电位器，电路也不会振荡.

这些都证明，共振吸收确实使样品的磁性发生了变化，即样品的磁矩发生了变化，使电路的电感发生变化.

5 铁磁共振试验的搭建

实验装置如图6，铁磁共振实际上是铁原子的电子自旋顺磁共振，在相同的外磁场中电子能级裂距约为核磁能级裂距的1840倍.所以能级间跃迁所需的能量要比核磁共振需要的能量hν（ν约为30MHz）大得多，因此实验用微波（约ν＝9GHz）来提供电子跃迁所需的能量.

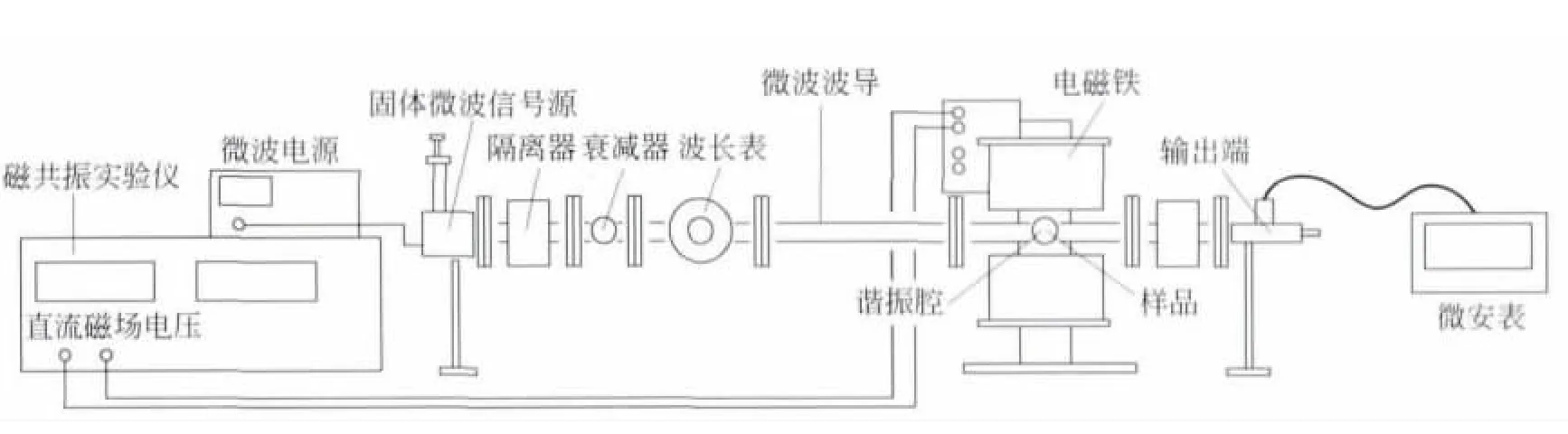
图6 铁磁共振实验的装置示意图

在实验中微波的频率ν是固定的，其在谐振腔的样品处磁场方向垂直于外磁场，能量hν也是固定的.

要产生磁共振，电子能级间的能量差γB必须等于该值，改变励磁电流值，使外磁场磁感应强度B变化，因而使电子能级间的能量差γB随之改变，当其接近于微波能量值hν时，电子就要吸收微波磁场的能量，产生铁磁共振，表现为检波二极管的输出电流减小，电流最小值对应的外磁场Br为谐振时的磁感应强度值，此时等式hν＝γBr成立，Br由实验所测得的共振吸收曲线求得，ν由波长表测出，γ即可求出.

这里检波二极管输出的电流正比于输入微波功率（见图7），没共振时，粒子不吸收微波能量，微波可完全越过粒子到达二极管，使其输出一个较大的电流.

图7 产生铁磁共振吸收曲线的装置简图

调节B，当粒子两能级间的能量差γB等于粒子处微波能量hν时，粒子吸收微波能量使输出电流减小，其最小值对应的外磁场Br即为核磁共振时的磁感应强度值.

6 结语

本文定性地讨论了大学物理核磁共振实验和铁磁共振实验的搭建思想，从基本原理出发分析了磁共振实验的搭建过程和实验装置各组成部分的物理作用.这样的分析讨论能使学生更清晰地了解实验的设计思想，拓展学生的知识，激发学生的学习兴趣，提高实验教学的水平和质量.

［1］李志超，轩植华，霍剑青.大学物理实验［M］.第三册.北京：高等教育出版社，2001：125-151.

［2］别业广，吕桦.再谈核磁共振在医学方面的应用［J］.物理与工程，2004，14（2）：34，61.

［3］霍剑青.应用信息技术培养创新型人才实验教学模式的思考与实践［J］.物理与工程，2013，23（6）：26-29，37.