“保守系统平衡位置微振动”案例教学的探讨与实践

宋海珍 王爱华 赵彤帆 李根全

（1南阳师范学院物理与电子工程学院，河南 南阳 473061；2河南省教育厅电教馆，河南 郑州 450004）

当前地方高等师范院校的理论力学教学中，由于师资质量和实践条件相对不足，知识的传授与掌握仍是教学目标的主要部分，传统的知识传授模式仍是主要的课堂教学模式.这种模式追求知识的完整系统而忽视探索过程、重视理论而忽视实践，它无法适应学生实践创新能力培养的现实需求［1］.案例教学作为一种典型的师生互动教学模式，可以弥补传统教学模式的缺陷，是创新本科课堂教学模式的有效途径［2-6］.理论力学作为高师物理学专业学生接触的第一门理论物理课程，其突出特点是理论性强，具有高度的抽象性和概括性，侧重于以严密的逻辑推理建立完整的理论体系.如何取舍内容，整合知识点，使之成为一个案例，直接影响到案例教学的成败.我们以周衍柏老师理论力学教材中“小振动”内容为基础［7］，联系我院实际，构成“保守系统平衡位置微振动”案例，对案例教学进行了探索和尝试.

1 案例教学的定义

案例教学是教师组织学生通过对案例的阅读、思考、分析、讨论、交流和评价等活动，提高学生分析、解决问题能力的一种教学模式［8］.它主要包括以下几个环节：（1）提出问题，介绍案例；（2）分析案例，提炼理论；（3）应用理论，审视案例；（4）评价总结，形成体系.通过这4个环节完成教学内容.

2 提出问题，介绍案例

为何讨论微振动？因为振动在机械、电磁（包括光）、原子和分子的运动中都普遍存在，它们具有许多相同的规律［9］.大多数机械振动的力学系统是非线性系统，不太可能对其运动得出完整的一般解，作为求解的试探，常常是对系统在平衡位置有微小偏离的运动求解，使非线性问题近似成为线性问题达到求解的目的，况且有些系统本身就是在平衡位置附近做微振动，例如分子或晶格处的原子［10］.对一维单自由度的振子，在无耗微振动时符合简谐振动的规律.如图1所示，一个弹簧和一个质点构成单自由度弹簧振子，两个弹簧和一个质点仍构成单自由度弹簧振子，对3个弹簧和两个质点构成的系统，是两个弹簧振子通过弹簧耦合的自由度为2的振动系统.对N＋1个弹簧和N个质点构成的系统就是N个弹簧振子的耦合系统，自由度为N［11-14］.（图中所有弹簧都相同，倔强系数为k，小球质量为m，弹簧质量、小球半径及水平面的摩擦均不计）.

对于两个或多个弹簧振子耦合在一起所构成的系统，各个振子可能有不同的固有频率，整个系统将怎样运动？它们将按某个或某几个统一频率振动？还是系统内各部分各行其是呢［15］？“保守系统平衡位置微振动”阅读思考提纲：（1）基本概念和方程：微振动、平衡位置、线性化近似、固有频率、简正频率、简正模式，拉格朗日方程、微振动方程、频率方程.（2）通过单个弹簧振子的求解得出单个自由度系统微振动理论.（3）通过两个弹簧振子耦合的求解，得出两个自由度系统微振动理论.（4）应用理论对N个弹簧振子耦合系统求解，检验完善理论.（5）评价总结，给出多自由度微振动的理论体系.

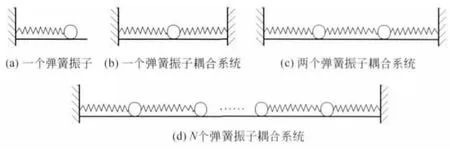
图1 弹簧振子系统

3 分析讨论案例，提炼理论

对“微振动”力学问题的分析，应向学生提出以下问题：（1）解决问题有几种途径？（2）各种途径的优劣比较？解决问题有矢量力学和分析力学两种理论.矢量力学求解时可用牛顿运动定律也可以用能量守恒；分析力学求解时可用拉格朗日方程也可用哈密顿方程.对自由度比较小的力学系统，牛顿运动定律和拉格朗日方程求解无大区别，对于自由度比较多的系统，拉格朗日方程相对牛顿运动定律来说较容易.

3.1 单个自由度微振动

3.1.1 两种途径求解

矢量力学求解：以图1（b）为例，选平衡位置为坐标原点，x为相对平衡位置的位移.只要弹簧是严格线性的，则f＝-2kx，由牛顿定律-2kx＝m，运动微分方程为

3.1.2 引导讨论

（1）平衡分几种类型？对振动问题有实际意义的是哪种平衡？保守系统稳定平衡所满足的条件？平衡分为稳定平衡（势能取极小值）、不稳定平衡（势能取极大值）和随遇平衡（势能取常数）3种类型.对振动问题有实际意义的是稳定平衡.保守系统稳定平衡位置需满足拉格朗日定理：自由度为1时，势能V满足是稳定平衡.对多自由度体系也有是稳定平衡.

（2）牛顿方程求解力的线性表示是微振动条件，而拉格朗日方程求解中动能、势能为、q的二次函数是微振动条件，两种条件等价吗？原因如何？为何要强调可线性化的微振动？两种条件等价，因拉格朗日方程中动、势能要对、q求偏导数.可线性化的微振动系统是经典力学中少有的可通过积分求严格解析解的几个系统之一（其他可积分系统如平方反比律作用的系统、自由刚体问题、对称陀螺等），不能线性化的振动系统需借助数值计算的方法确定系统运动情况，有兴趣的同学可编程计算单摆小角摆动、大角摆动运动微分方程的求解.

3.1.3 提炼理论

对于单个自由度的保守系统，q为广义坐标，则将势能V（q）在q0＝0附近作泰勒展开，选q0处为零势能点，仅保留q的二阶项：由拉格朗日方程得到：方程的解为：

3.2 两个自由度微振动

两个弹簧振子的运动是耦合的，方程也是耦合的，求解方程组（2）的方法有几种呢？答案是3种.方法一为试探解，是一种基本方法；方法二是对微分方程分析变形；方法三是动、势能化为平方和的形式.

3.2.1 3种方法求解方程组

方法一：设试探解为

式（3）代入式（2）得到A1、A2的代数方程组得

式（4）有解的条件是

式（6）代入式（4），对ω1，有A1＝A2；对ω2，有A1＝-A2，微分方程组（2）的通解为

方法二：直接对方程组（2）变形求解，对方程组（2）中的两个方程分别相加、减得到

式（9）的通解是两个谐振动

方法三：直接把动、势能化为平方和.一般情况下，根据线性代数理论，如果两个二次型的系数是实对称的，其中一个是正定的，则一定可以找到一个线性变换，使两个二次型同时变为平方和.微振动的动、势能满足条件，一定存在一个x和ξ的线性变换，代入动、势能中让交叉项系数等于零，就可把动、势能化为平方和的形式，进而用拉格朗日方程得到单一振动模式的动力学方程.设组（9）.

3.2.2 引导讨论

（1）总结简正频率、简正坐标、简正模式的概念，分析为何试探解式（3）中cos（ωt＋φ）都相同呢？不同行吗？答案是必须相同.从数学上讲，这正是线性齐次微分方程的特点，用不同的cos（ωt＋φ）则不能满足方程组，方程组（2）各项含t的因子不能相消，最多只能在某些时刻为零.从物理上讲，不同的ω对应不同的振动频率，若式（3）中各项的ω不同，则它们对应不同频率的振动，不同频率振动的任意线性组合都不可能等于零，即方程组（2）中各个方程不能成立.

（2）两个简正振动模式分别代表何种运动？对简正振动模式ω1：ξ1＝x1＋x2＝A1cos若表示两质点同相振动，反映整体振动情况.对简正振动模式ω2：若x1（0）＝则有ξ1＝0，ξ2＝2x0cosω2t，表示两质点反相振动时的相对运动，ξ2表示1对2的相对运动，反映两个振子通过中间弹簧耦合的情况.

（3）系统的任一振动与简正振动的关系？系统的任一种振动状态是各种简正振动的线性叠加，看初始时哪些被激发，哪些没有激发？若初始只激发一个，其余没有激发，就只有一个简正模式振动，简正坐标不仅使方程求解容易，而且反映了系统振动的物理本质.对于一个微观系统，由于热运动引起的能量涨落，以致温度足够高，各简正模式都会在一定程度上激发起来.在这种意义下，简正模是凝聚态物理学中重要概念“元激发”的萌芽.

（4）耦合效应使共同频率ω0分成两个不同本征频率ω1和ω2，若m2固定，m1振动，则ω0＝固定，m2振动，则两个振子没有耦合时振动情况完全相同，具有相同的振动频率ω0，耦合效应使ω0分成ω2和ω1两个频率.

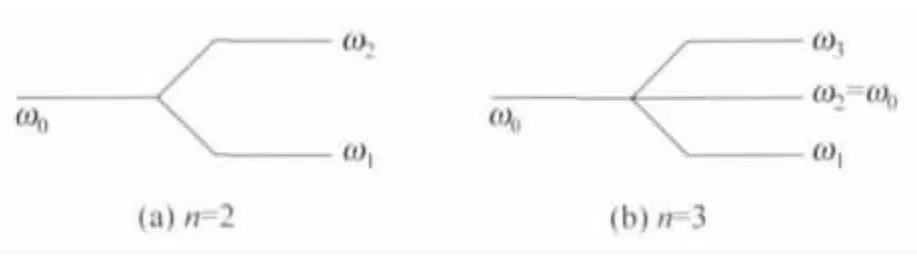
图2 耦合弹簧振子的频率

如图2（a）所示，这种频率的分裂类似于原子光谱中的塞曼效应，在那里相互作用是通过施加磁场.如果对于3个质点，4个弹簧构成的系统，通过类比猜想或求解，也得到本征频率分成图2（b）所示.

3.2.3 提炼理论

对两个自由度的保守系统，q1，q2为广义坐标，势能在平衡位置处展开，线性近似略去高于二阶的微量，引入对稳定约束力学系统：利 用广义速 度变换，代入拉格朗日方程

式（12）有解的条件是

4 应用理论，审视案例

4.1 应用理论

通过类比，把两个微振动求解理论应用到N个自由度微振动系统，如图1（d）所示，选qs（表示某一瞬时第s个质点偏离平衡位置位移，s＝1，2，…，N）为广义坐标，因边界是固定的，q0＝qN＋1

设试探解为

在近代物理中，用复数表示简谐振动比较方便，复数的实部或虚部就是经典力学中的谐振动.

式（15）的A可以是复数，与位置无关，qs＝sa是第s个质点平衡时的位置，a是平衡时相邻两质点间的距离.k波（波矢）和φ（相位）由边界条件决定.确定ω：式（15）代入式（14）得mω2＋k（e-ik波a-2＋确定φ：由q0任何时候都成立，得eiφ＝0，或它们的奇数倍，取保证式（15）中qs实部不出现负号.确定k波：由qN＋1＝任何时候都成立，则k波（N＋1）a＝απ，α＝1，2，…，N.得其中，α＝1，2，…，N，式（15）的实部解为

可见，对N个自由度的系统，解决的方法步骤与两个质点完全相同，有几个自由度，就有几个简正频率，也就有几个简正模式和简正坐标.

4.2 拓展与延伸

N个质点系统在固体物理中用来研究一维晶体振动性质，它反映系统在最近邻相互作用下的特性：

不出现质点的序号s，证明系统中所有质点都具有这种频率与波矢的关系，通常称为色散关系.ωα的最大值表示质点振动频率增加到（ωα）max时自然截止，频率大于（ωα）max的振动不可能在一维系统中存在并传播.

（3）经典力学方法求解一维N体振动，其结果部分说明晶体的性质，对晶体性质的全面描述，必须用量子理论描述.简正坐标描述的一维谐振子，量子力学处理方法中把力学量用算符表示，得到量子力学描述，谐振子能量是分立的，定义分立能量hωα为声子，声子是晶格集体激发的玻色型准粒子，它具有能量hωα和准动量hk波.

（4）对两个或多个弹簧振子耦合的系统，整个系统不按某个或某几个振子的频率振动，而是存在简正振动模式，且按简正频率振动，系统任意振动是这一系列简正振动的线性叠加.

5 评价总结，形成理论体系

结合单自由度、两个自由度微振动的处理方法，我们用拉格朗日方程给出s个自由度保守系统微振动的一般理论.对s个自由度的力学系统，受保守力稳定约束，相对平衡位置qα0＝0的广义坐标qα，α＝1，2，…，s，势能在qα0附近展开，线性近似后，设有V＝将L＝T-V代入拉格朗日方程，得到设试探解qβ＝Aβcos（ωt＋α），β＝1，2，…，s，代入运动微分方程得这是关于振幅Aβ的方程组，Aβ有非零解必须满足频率方程

小振动的频率不能任意取值，只能由频率方程确定.它是ω2的s次方程，一般有s个根，这些根与振动的初始条件无关，仅决定于惯性和劲度系数，也叫力学系统的固有频率，固有频率求出后，代入振幅Aβ方程，确定s个Aβ的比值，进而得到对应的某一频率的特解.因微振动的动力学方程是线性的，故整个力学系统的解一定是这些特解的线性组合.理论的使用条件是：保守系统，稳定约束，可线性化处理.

6 结语

地方高等师范院校专业课中的案例教学，有利于从问题出发，促成学生成功的体验，激发主动学习的积极性，提高学生的综合素质和创新实践能力.通过多阶段的案例分析实践过程，不仅使理论来源于实践，应用于实践，在实践中强化理论的应用和理解.而且通过案例整合知识，使知识应用整体化，打破了力学、理论力学和固体物理学中各部分知识相对独立的局面.同时对师范生的教育教学技能进行了培养，起到了示范课的作用.但由于案例教学的难度大，需要教师广博深厚的专业知识，花费更多时间，投入更多的精力.需要学生做好课前阅读和思考，才能达到较好的效果.在地方高师院校中，部分学生有畏难情绪，放弃课前阅读思考，教师要对课前阅读思考状况准确地把握及时指导，课堂上才会有较好的交流互动.

［1］王华荣.以案例教学推动大学课堂教学模式改革的实践与探索［J］.中国大学教学，2011（4）：62-64.

［2］张萍，刘宇星.同伴教学法在大学物理课程中的作用［J］.物理与工程，2012，22（1）：41-43.

［3］王翀，梁猛，杨祎.一种创新实践教学模式［J］.实验室研究与探索，2011，30（7）：152-154.

［4］段志刚，彭志敏.大学物理探究性教学设计策略与方法［J］.物理与工程，2012，22（3）：54-56.

［5］刘良成，许秀英，刘健.研究型教学的探讨与尝试［J］.实验室研究与探索，2011，30（10）：293-295.

［6］高虹.从美国理工科本科教学改革看研究型教学［J］.物理与工程，2004，14（2）：12-14.

［7］周衍柏.理论力学教程［M］.3版，北京：高等教育出版社，2009：224-231.

［8］郭易圆，彭慧莲，王琪.理论力学探究型教学模式的探索与实践［J］.力学与实践，2011，23（3）：70-72.

［9］金尚年，马永利.理论力学［M］.2版，北京：高等教育出版社，2002：172-207.

［10］鞠国兴.理论力学学习指导与习题解析［M］.北京：科学出版社，2008：220-267.

［11］鲁兴举，彭学锋，郑志强.提高自动化专业学生工程素质——以倒立摆实验为例［J］.实验室研究与探索，2011，30（10）：272-275.

［12］刘正波，夏清华，刘思平.不同控制参数下的弹簧摆［J］.大学物理，2011，30（5）：23-26.

［13］尹新国，柯远贵，公丕锋，等.倒置摆的运动研究［J］.大学物理，2011，29（11）：16-20.

［14］柯正波，夏清华，刘思平.多弹簧振子耦合系统运动研究［J］.大学物理，2010，29（4）：29-32.

［15］赵凯华，罗蔚茵.力学［M］.2版，北京：高等教育出版社，2004.249-260.

［16］胡安，章维益.固体物理学［M］.2版，北京，高等教育出版社，2011.78-96.