范德瓦尔斯气体的气压公式

蓝风华

（武警工程大学理学院，陕西 西安 710086）

大学物理教科书中，一般都给出了理想气体恒温气压公式［1］

其中，M为气体摩尔质量，T为热力学温度，p0为地面高度h＝0处的压强.

实际上大气温度是随地面高度而变化的，同时理想气体与大气实际气体也有出入，因此用式（1）计算出的压强只能是近似结果.为了得到比较接近实际的结果，不妨将大气近似为范德瓦尔斯气体，用多方过程取代等温过程，这样推导出的气压公式会更接近实际.

1 范德瓦尔斯气体的多方过程

设1mol范德瓦尔斯气体的压强为p，体积为V，温度为T，其状态方程为

其中，R为普适气体常数；a、b为范德瓦尔斯修正量.

由热力学第一定律

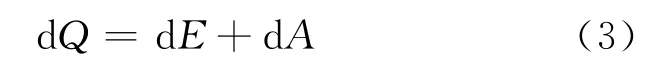
其中，

式中，C为摩尔热容；CV为等体摩尔热容，它们都是温度的函数.通常实际问题中，由于温度变化不大，C、CV变化很小，因而近似视作常量.

式（3）即为再利

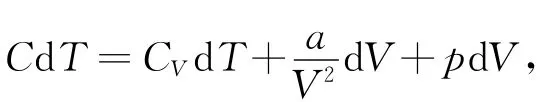
用式（2）可得

对上式积分并整理，可得范德瓦尔斯气体的多方过程的T、V关系为

利用式（2）还可得到多方过程的p、V关系，即

若令

则式（4）、（5）可分别写成

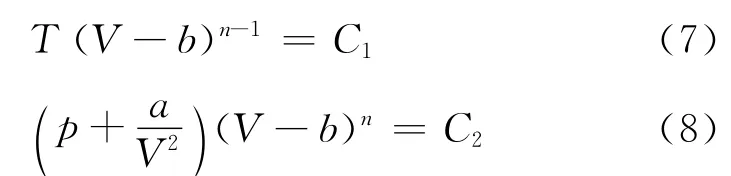
通常称n为多方指数.

2 范德瓦尔斯气体的气压公式推导

如图1所示，设在高度h处有一薄层空气，其底面积为S，厚度为dh，上下两面的气体压强分别为p＋dp和p，该处空气密度为ρ，根据力学平衡条件

即

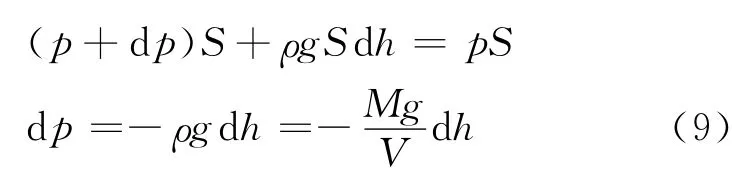
其中，V为摩尔体积，M为摩尔质量

图1 空气层受力图示

若将大气近似为范德瓦尔斯气体，则由式（8）中的p代入式（9），可得

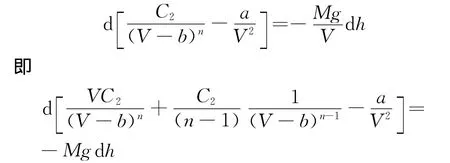
利用式（8）和式（2），上式还可得

再利用式（7）消去V，可得

设地面高度为零时，温度为T0，摩尔体积为V0；地面高度为h时，温度为T，摩尔体积为V，对式（10）两边积分，并利用式（7），可得

式（11）反映了温度随高度变化的函数关系.

由式（2）及式（7）可得范德瓦尔斯气体处于多方过程的气压公式为

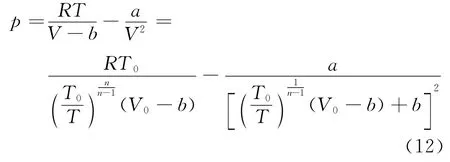
式（12）反映了压强随温度T即随高度h变化的函数关系.

3 讨论

1）若将大气视为理想气体，则a＝0、b＝0，式（11）变为

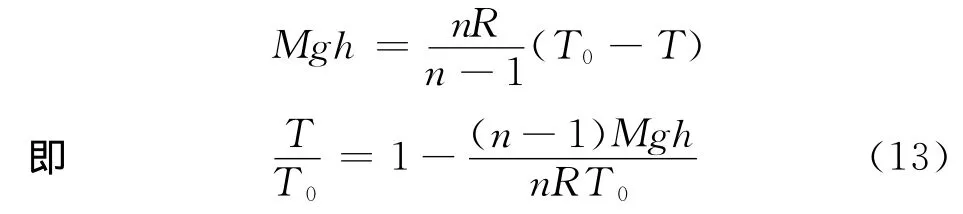
将式（13）代入式（12）可得

它与文献［2］的结果一致.即在同一高度下，压强随多方指数的增加而减少.

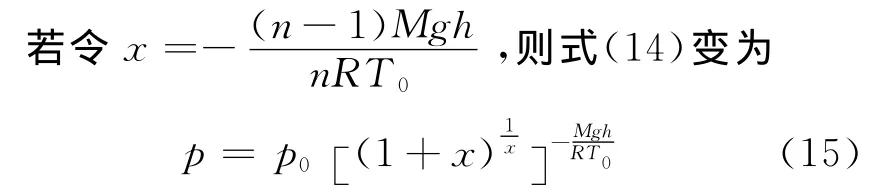
当n→1，即x→0时，式（15）变为

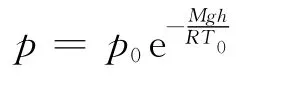
这正是理想气体的恒温气压公式.

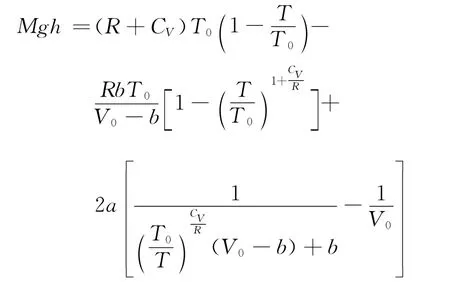
式（12）变为

它与文献［3］结果一致.

若将大气视作理想气体绝热模型，则式（14）变为

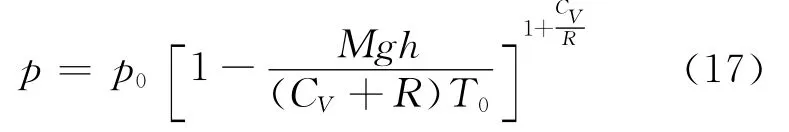
对于范德瓦尔斯气体与理想气体的绝热过程的气压公式的比较，文献［3］做了详细的阐述，本文就不一一赘述.

总之，范德瓦尔斯气体处于多方过程的气压公式，确实是对理想气体气压公式的一种很好的修正.

［1］张三慧.大学物理：第二册［M］.2版.北京：清华大学出版社，1999：14.

［2］魏国柱，顾永伟，杜安.对气体等温气压公式的修正［J］.大学物理，2006，25（17）：28.

［3］穆良柱，史寒朵.重力场中的范德瓦尔斯气体［J］.大学物理，2011，30（10：）：5-6.