Fε-I类凸半无限规划的最优性

杨 勇

(陕西科技大学 理学院， 陕西 西安 710021)

0 预备知识与新广义凸函数的定义

凸函数在最优化理论中起着重要作用，近年来已得到各种形式的推广，并由此得到众多的广义凸函数类.其中有两大类广义凸函数值得关注.其一就是由Hanson和Mond[1]首次引入的Ⅰ类和Ⅱ类广义凸性函数，这些广义凸函数也被应用于非线性规划、半无限规划等各类规划问题.随后，这两类函数又多次被进一步的推广和应用[2-5].另一大类就是由孙永忠和康开龙[6]引入的广义凸函数；Liang Z A等[7]将其推广为(F,α,ρ,d)-凸函数.随后，这些函数也得到了各种形式的推广和应用[8-12].

受这些文献的启发,本文首次引入Fε-I类、拟Fε-I类和伪Fε-I类等广义凸性概念，并在这些广义凸性假设下，研究下列半无限规划问题:

其中U⊆Rm是一个无限参数集，记

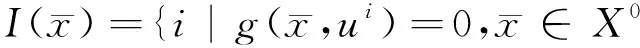
Ω={λi|λi≥0,i∈Δ,仅有有限个λi≠0}，

Δ={i|g(x,ui)≤0,x∈X0,ui∈U},

X={x|g(x,ui)≤0,x∈X0,ui∈U⊆Rm},

U*={ui|x∈X0,g(x,ui)≤0,ui∈U,i∈Δ}

为U的任意可数子集.

为了方便起见，在下文中我们设函数g:X0×U→R,f:X0→R是局部Lipschitz的，对于局部Lipschitz函数f,它在x0处沿方向d的广义方向导数和广义梯度如下：

∂f(x0)={ξ∈Rn:〈ξ,d〉≤f(x0,d),∀d∈Rn}

在下文中，我们还要用到次线性函数的概念，函数F:X0×X0×Rn→R是次线性的，即对∀x1,x2∈X0函数F满足下列条件：

F(x1,x1,α1+α2)≤F(x1,x1,α1)+F(x1,x1,α2),∀α1,α2∈Rn

F(x1,x1,rα)=rF(x1,x1,α),∀α∈Rn,r∈R+

定义1设函数F：C×C×Rn→R为次线性的，称(f,g)在u∈X0处是Fε-I类凸的，若对∀x∈X0,∀ε,εi>0有：

f(x)-f(u)≥F(x,u,ξ)+ε∀ξ∈∂f(u)

(1)

-g(u,ui)≥f(x,u,η)+εi∀η∈∂g(u,ui)

(2)

若(f,g)在X0中的任意一点都是Fε-I类凸的，则称(f,g)在集X0上是Fε-I类凸的.若当x≠u时，不等式(1)是严格不等式，则称(f,g)在u∈X0处或者在X0上是半严格Fε-I类凸的.

定义2设函数F：C×C×Rn→R为次线性的，称(f,g)在u∈X0处是拟Fε-I类凸的，若对∀x∈X0,∀ε>0,εi>0及一些λi∈Ω有：

f(x)-f(u)≤0⟹F(x,u,ξ)+ε≤0

∀ξ∈∂f(u)

(3)

∀η∈∂g(u,ui)

(4)

若(f,g)在X0中的任意一点都是拟Fε-I类凸的，则称(f,g)在X0上是拟Fε-I类凸的.若当x≠u时，(3)式中的第二个不等式是严格的，则称(f,g)在u∈X0处或者在X0上是严格拟Fε-I类凸的.

定义3设函数F：C×C×Rn→R为次线性的，称(f,g)在u∈X0处是伪Fε-I类凸的，若对∀x∈X0,∀ε>0,εi>0及一些λi∈Ω有：

F(x,u,ξ)+ε≥0⟹f(x)-f(u)≥0

∀ξ∈∂f(u)

(5)

∀η∈∂g(u,ui)

(6)

若(f,g)在X0中的任意一点都是伪Fε-I类凸的，则称(f,g)在X0上是伪Fε-I类凸的.若当x≠u时，(6)式中的第二个不等式是严格的，则称(f,g)是严格伪Fε-I类凸的.

定义4设函数F：C×C×Rn→R为次线性的，称(f,g)在u∈X0处是伪拟Fε-I类凸的，若对∀x∈X0,∀ε>0,εi>0及一些λi∈Ω有：

F(x,u,ξ)+ε≥0⟹f(x)-f(u)≥0

∀ξ∈∂f(u)

(7)

∀η∈∂g(u,ui)

(8)

若(f,g)在X0中的任意一点都是伪拟Fε-I类凸的，则称(f,g)在X0上是伪拟Fε-I类凸的.若当x≠u时，(7)式中的第二个不等式是严格的，则称(f,g)在u∈X0处或X0上是严格伪拟Fε-I类凸的.

定义5设函数F：C×C×Rn→R为次线性的，称(f,g)在u∈X0处是拟伪Fε-I类凸的，若对∀x∈X0,∀ε>0,εi>0及一些λi∈Ω有：

f(x)-f(u)≤0⟹F(x,u,ξ)+ε≤0

∀ξ∈∂f(u)

(9)

∀η∈∂g(u,ui)

(10)

若(f,g)在X0中的任意一点都是拟伪Fε-I类凸的，则称(f,g)在X0上是拟伪Fε-I类凸的.若当x≠u时，(10)式中的第二个不等式是严格的，则称(f,g)在u∈X0处或X0上是严格拟伪Fε-I类凸的.

1 最优性条件

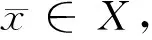
∀ξ∈∂f(x0)

(11)

又由题设②中函数的凸性可知：

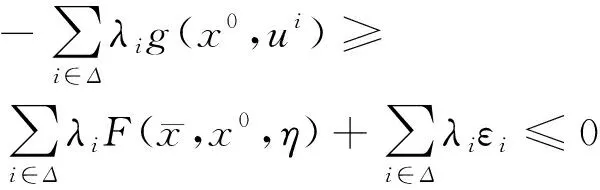
∀η∈∂g(x0,ui)

由函数F的次线性性质可得：

由此可得：

∀η∈∂g(x0,ui)

(12)

将(11)式与(12)式相加，并由函数F的次线性性质可得：

∀ξ∈∂f(x0),∀η∈∂g(x0,ui)

(13)

当i∈I(x0)时，g(x0,ui)=0;当i∈ΔI(x0)时，由题设①可知λi=0,从而有：

结合(13)式可知

∀ξ∈∂f(x0),∀η∈∂g(x0,ui)

但根据题设可知

∃ξ′∈∂f(x0),η′∈∂g(x0,ui)使得

这是一个矛盾!所以x0为规划(SIP)的最优解.

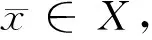
∀ξ∈∂f(x0)

(14)

∀η∈∂g(x0,ui)

当i∈ΔI(x0)时，由题设①可知λi=0从而有

∀η∈∂g(x0,ui)

所以有

∀η∈∂g(x0,ui)

(15)

将(14)式与(15)式相加，并由函数F的次线性性质可得

∀ξ∈∂f(x0),∀η∈∂g(x0,ui)

由此可得

∀ξ∈∂f(x0),∀η∈∂g(x0,ui)

这与题设矛盾，所以x0为规划(SIP)的最优解.

类似可以证明下列定理.

[1] Hanson M A.On sufficiency of the Kuhn-Tucker condition[J].J.Math.Anal.Appl,1981,80:545-550.

[2] Jeyakumar.V,Mond.On generalized convex mathematical programming[J].J.Austral Math.Soc.ser B,1992,34(1):43-53.

[3] Kaul.R.N,Suneja S.K.Optimality criteria and duality in multiple objective optimization involving generalized invexity[J].J.Optim.Theory Appl,1994,80:465-482.

[4] 李 伟,张可村.一类不可微广义凸多目标规划的最优性条件和对偶[J].工程数学学报,2012,29(3)：419-422.

[5] 张庆祥，刘鹏辉．一类广义J类不变凸半无限规划的最优性条件[J]．延安大学学报(自然科学版)，2002，21(4)：1-4．

[6] 孙永忠,开龙非.滑广义F-凸多目标半无限规划的最优性条件[J].工程数学学报,1996,13(1):117-121.

[7] Liang Z A,Huang H X,Pardalos P M.Optimations and duality for a class of nonlinear fractional programming problems[J].JOTA,2001,110(3):611-619.

[8] 杨 勇,连铁艳,穆瑞金.凸分式半无限规划的最优性[J].西南师范大学学报(自然科学版),2008,33(6):1-4.

[9] 杨 勇.凸分式半无限规划的最优性条件[J].辽宁师范大学学报(自然科学版),2009,30(3)：280-283.

[10] Yong Yang.Optimality solutions for a class of convex fractional semi-infinite programming[C]//Proceedings of 3rd International Joint Conference on Computational Sciences and Optimization.Los Alamitos:IEEE Computer Society,2010:13-15.

[11] Yong Yang,LiHua Liu,TieYan Lian.Duality in fractional semi-infinite programming withconvexity[C]//Proceedings of 3rd International Conference on Information and Computing.Edgbaston:World Academic Press of WAU,2010:37-39.

[12] 高晓艳.某些非光滑半无限规划的最优性与对偶性[D].延安：延安大学，2005．