高等代数中的反例研究

谢余波

(咸宁市高级中学，湖北 咸宁 437100)

一、基于弱化命题条件下的反例研究

高等代数中的命题有些条件是必不可少的。当弱化命题条件时，会降低结论的可靠性，甚至会导致命题的错误。因此这就要求我们对命题的条件尽可能的简化，抓住中间最主要的推理关系，只要命题中缺少必要的条件时，就可以对结论得以反驳。而推翻结论需采用列举反例的证明方法，即举出特定的例子来加以说明。以下通过弱化命题条件得出了关于多项式的整除、不可约多项式、线性方程解及空间直和的反例。

命题1.1 如果h(x) 整除f(x)·g(x)，且(h(x),f(x))=1，那么h(x)整除g(x)。但是，当一个多项式整除两个多项式之积时，如果没有互素的条件，这个多项式一般不能整除因式之一。

例设h(x)=x2-1,f(x)=(x+1)2,g(x)=(x-1)2,显然h(x)与f(x)或g(x)都不互素。h(x)整除f(x)·g(x),但h(x)不整除f(x)且h(x)不整除g(x)。

命题1.2 设p(x)是一个不可约多项式，而f(x)是一个任意多项式，那么，或者(p(x),f(x))=1，或者p(x)整除f(x)。若p(x)是可约多项式，则上述性质不成立。

二、基于逆命题的反例研究

高等代数中充要命题有利于解决有关性质和判定的命题。但并非所有的命题都是充要的，本节通过列举有关数域、多项式不可约性、实对称矩阵等反例，对原命题的逆命题的成立性进行了深入的探讨。

命题2.1 设f(x)≠0,h(x)为任意多项式，若(f(x),g(x))=1，则(f(x),g(x)h(x))=(f(x),h(x))，反之不真。

例则有f(x)=x2-1,g(x)=(x+1),h(x)=(x-1)2(x+1)，则有(f(x),g(x)h(x))=(f(x),h(x))=x2-1,但是(f(x),g(x))=x+1≠1。

命题2.2 如果次数≥2的有理系数多项式有有理根，那么在有理数域上它一定是可约的，反之则不然。

例f(x)=x4-4在有理数域上，有f(x)=(x2-2)(x2+2)，所以是可约的，但它无有理根。

三、基于存在性的反例研究

命题3.1[12]艾森斯坦判别法告诉我们：当f(x)=anxn+an-1xn-1+…a0是一个整系数多项式，存在一个素数p，使得：1.p不整除an

2.p/an-1,an-2,a0

3.p2不整除a0.

那么f(x)在有理数域上是不可约的。可是当我们找不到这样的素数p，我们便不能判定其是否是可约的。

例f(x)=x2+3x+2,g(x)=x2+1，对f(x)及g(x)来说，都找不到满足判定法条件的素数p，但f(x)在有理数域上是可约的，g(x)不可约。

四、基于矩阵性质的反例研究

矩阵是高等代数中的一个重要概念，它在其中占有突出的重要的位置，矩阵理论也是高等数学许多分支的不可缺少的工具，在处理许多实际问题上也是很有力的，而我们在学习一个新的知识的时候，为了弄清楚它的性质，往往会选择联系我们之前学过的内容，有时可以起到加强知识点的作用，但不合理的沿用之前的结论或无限的延伸结论往往会得到一些错误的命题。下面举出一些相关的反例。

命题4.1 存在零因子，即A≠0，B≠0，但AB=0。

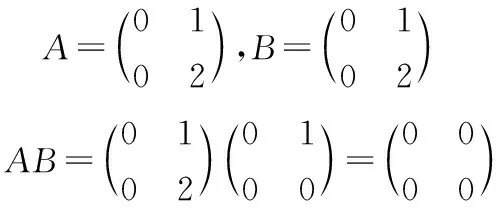
命题4.2 矩阵乘法的消去律不成立，即A≠0，AB=AC，未必有B=C。

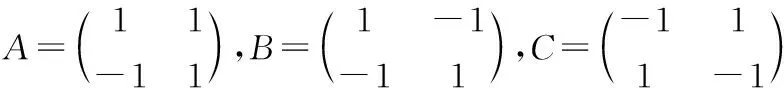
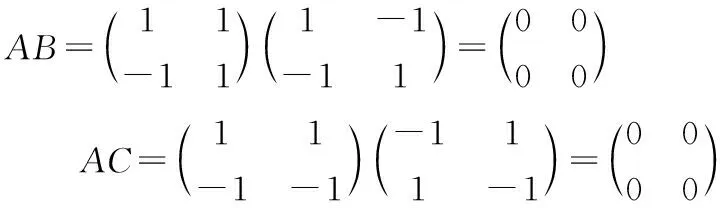
于是AB=AC，且A≠0，但B≠C。

五、基于λ-矩阵特殊性的反例研究

λ-矩阵作为一种特殊的矩阵，它与一般的数字矩阵既有联系又有区别，数字矩阵为λ-矩阵的零次矩阵，而λ-矩阵一般定义上不包含数字矩阵，故其性质往往有所差异，数字矩阵满足的一些性质及关于数字矩阵的一些定理不可以延拓到λ-矩阵，下面就列举一些有关λ-矩阵特殊性质的一些反例。

命题5.1 对于数字矩阵而言，满秩与可逆等价，但对于n阶λ-矩阵，满秩不一定可逆。

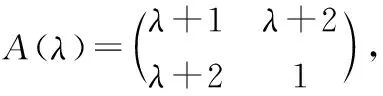
命题5.2 数字矩阵如果满秩，则可表为一系列初等矩阵之积，但满秩λ-矩阵不一定能这么做。

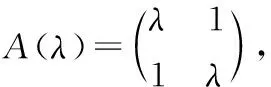
在社会实践和学习的过程中，当我们对一个问题苦思冥想而不得其解时，从反面想一想，常能获得意外的收获。本文就通过综合论述高等代数中五种常见类型的反例，加深了对书中定理和定义的理解和认识，并在此基础上灵活运用于相关的命题中，解决实际生活中的问题。