基于DCT和分块2D2PCA的人脸识别

张秀琴，陈立潮，潘理虎，2，谢斌红

(1.太原科技大学，太原 030024；2.中国科学院地理科学与资源研究所，北京 100101)

人脸识别特指利用分析比较人脸的特征信息进而进行身份鉴别的计算机技术，是一种重要的生物特征识别技术，也是模式识别与图像处理领域的研究热点之一[1]，文献[2-3]讲述了人脸图像识别的主要方法和进展。随着计算机的发展又出现了3D人脸重建和动态特征提取的人脸识别[4]、方法和机器的自动人脸识别[5]、多尺度局部相位量的融合[6]、基于统计学习的人脸识别[7]等人脸识别方法。虽然已经提出了很多人脸识别的算法，但这些算法的性能仍然需要进一步改进。在已有的人脸识别算法中，DCT余弦变换被广泛应用[8-10]。主成分分析法[11](PCA，Principal Component Analysis)又被称为K-L变换，被广泛的认为是成功的线性鉴别法之一。PCA方法不仅能降低人脸图像矩阵的维数，又能保留用于人脸识别的主要信息。但该方法必须将人脸图像转换为一维向量，然后将转换后的一维向量作为原始特征进行提取。由于转换之后的向量维数较高，使得特征提取变得更加困难，后续计算更加复杂。YANG等人提出了二维成分分析(2DPCA)方法提取人脸面部特征[12]，该方法不需要将人脸图像阵转化成一维向量，有效的减少了后续计算的复杂度，文献[13]和文献[14]提出了DCT和2D-PCA相结合的改进算法，有效地保留了对光照、人脸表情以及人脸姿势不敏感信息并缩短了识别的时间；但特征提取的计算量较大[15]；在2009年双向主成分分析法[16]((2D)2PCA，two directional two dimensional Principal Component Analysis)被提出，此算法利用二维PCA方法对人脸图像矩阵的行方向、列方向分别进行降维，得到人脸图像的特征信息；文献[17]应用2D2PCA得到行和列两个不同方向上的人脸图像映射矩阵，并降低了所得特征矩阵的维度，但表征人脸特征的信息不全面，文献[18]提出了加权分块(2D)2PCA方法，应用(2D)2PCA和图像分块思想得到比较全面的人脸特征信息但识别率较差；鉴于此，本文提出了一种基于DCT与分块(2D)2PCA方法进行人脸图像特征的提取并识别人脸图像。

1 算法原理

1.1 二维离散余弦变换

二维离散余弦变换[8](DCT ，Discrete Cosine Transform)，是一种与离散傅里叶变换(DFT for Discrete Fourier Transform)相关的变换，它仅仅用到了实数中。离散余弦变换长度相当于一个两倍于它的离散傅里叶变换。此离散傅里叶变换是对一个实偶函数进行的变换，设图像A的尺寸为M×N则二维离散余弦变换(DCT)定义为：

(1)

其中，Bp,q称为矩阵A的DCT系数，m=0，1，…，M-1；n=0，1，…，N-1；p=0，1，…，M-1；q=0，1，…，N-1；ap，aq的表达式：

(2)

(3)

二维离散余弦变换(DCT)的特点是：图像经DCT变换后，数值大的频谱系数主要集中在DCT系数比较小的范围且其主要分布在频谱较小的左上角区域，这说明有用信息有集中区域，如下图。基于DCT系数重建图像，保留了少数的低频分量 ，而舍掉大部分的高频分量。

图1 人脸原图像及其DCT系数Fig.1 Face image and DCT coefficients

1.2 二维离散余弦逆变换

二维离散余弦逆变换(IDCT)[8]是二维离散余弦变换(DCT)一种可逆变换，则逆变换定义为：

(4)

其中，A称为矩阵Bp，q的IDCT系数，m=0，1，…，M-1；n=0，1，…，N-1；p=0，1，…，M-1；q=0，1，…，N-1，ap，aq的表达式如公式(2)和公式(3)：

利用IDCT，可获得与原始图像相近的重建图像，重建图像与原图像存在一定的差异，但重要的信息都被保存了下来，如图2所示。

图2 原图像和重建图像Fig.2 Face image and the reconstructed face image

1.3 分块(2D)2PCA

1.3.1 2D2PCA

二维主成分分析(2DPCA)[11]是为了缩短提取图像特征的时间和减少训练PCA的时间而提出来的计算方法，此方法直接进行计算二维图像的矩阵，不像PCA方法需要把图像矩阵转换为一维向量，求特征值的计算量大大的减少了。2DPCA的方法直接在二维图像矩阵上得到了协方差矩阵，并求的该协方差矩阵的特征值和特征向量，并将二维图像直接投影到计算出的最优投影方向上，得到一组投影的特征向量。人脸识别中应用的2DPCA被分为特征提取和模式的分类。

二维主成分分析(2DPCA)是提取图像特征的一种方法，算法由图像矩阵得到训练样本图像的总体散布矩阵(协方差)，然后，计算总体散布矩阵的特征值和特征向量。而双向的2DPCA算法[15]是2DPCA的一种，具体算法如下：

设图像矩阵A为M×N，通过线性变换Y=AX将A投影到X上得到一个维度为M维列向量Y，被称为A的投影特征向量。在训练样本中Xij表示第i个人的第j幅图像，则样本的平均值K定义了：

(5)

其中I和J表示训练样本选取的类数和每类的图片数。则可得到样本的协方差矩阵G：

(6)

求出G的特征向量即前d个最大特征值所对应的标准正交特征向量v1v2，…，vd.得到的最优投影矩阵V=(v1v2，…，vd)消除图像矩阵行相关性。为消除图像矩阵列相关性，可由样本的另一协方差矩阵Z，按下式(7)重新求得投影矩阵U：

(7)

计算协方差Z的特征向量即计算得前t个最大特征值所对应的标准正交特征向量分别为u1，…，u2，ut.组成另一个最优投影矩阵U=(u1，…，u2，ut)，消除图像矩阵列相关性，则可得到训练样本的特征矩阵为：

Cij=UTXijV

(8)

将每个训练样本图像同时投影到最优投影矩阵U和V上，得到了训练样本的特征矩阵Cij如公式(8)所示，同样选定一幅测试图像A1，将A1投影到上述所计算的最优投影矩阵U和V上则可得到其特征矩阵C1.

1.3.2 分块(2D)2PCA

分块(2D)2PCA的思想是将一个M×N的图像A矩阵分成p×q个模块的图像矩阵，其中，每个子图像矩阵Ak1是m1×n1矩阵，pm1=M，qn1=N，然后将所有的子图像矩阵看作训练样本，进行(2D)2PCA运算。设有c种类别，分别为ω1，ω2，…，ωc，每个训练样本是M×N矩阵。则所有的训练样本数为W：

(9)

训练样本A的p×q个模块，则训练图像样本的子图像行方向的总体散布矩阵Gcolumn，而训练图像样本的子图像列方向的总体散布矩阵Grow.

(10)

(11)

其中，S=Wpq表示训练样本的子图像矩阵总数，B表示所有训练样本的子矩阵均值矩阵。

(12)

求式(11)(12)行方向、列方向的协方差矩阵的标准正交特征向量即分别计算不同协方差的前d个，前t个最大特征值所对应的标准正交特征向量，V=(v1，v2，…，vd)，U=(u1，u2，…，ut)为最优投影矩阵。然后对训练样本Ai进行特征抽取，则:

(13)

的特征矩阵为Ci：

(14)

若被测试的图像矩阵为A：

(15)

则A的特征矩阵为C：

(16)

1.4 最近邻分类法

通过以上公式(14)、公式(16)提取特得到了训练样本图像矩阵对应的特征矩阵Ci=UT(Ai)klV和测试图像矩阵对应的特征矩阵C=UT(Ai)V，则利用最近邻分类法，特征矩阵Ci与C之间的距离定义为d，实现了图像的分类识别。

d(C,Ci)=‖C-Ci‖

(17)

同时在此实验中，定义了识别相似度，所得距离d为0时，相似度被认为是100%.因此d较大时，通常认为样本图像和测试图像之间没有相似之处。所以本文把d按从小到大的顺序排列且排列在第十个的d值定义为相似度为0%，因此得到相似度为(1-di/d10)×100%.

2 本文算法的人脸识别

本文首先利用二维离散余弦变换(DCT)对训练人脸图像和测试人脸图像分别进行了压缩，去除图像中干扰冗余的信息，保留了有用的特征信息后再利用二维离散余弦逆变换(IDCT)对图像进行重建。然后将重建的人脸图像分成p×q个模块的图像矩阵，并对每一个模块运用2D2PCA得到特征矩阵，2D2PCA在分块的行、列两个方向上分别消除图像数据的相关性。再利用最近邻分类法识别人脸图像，算法流程如下图3所示。

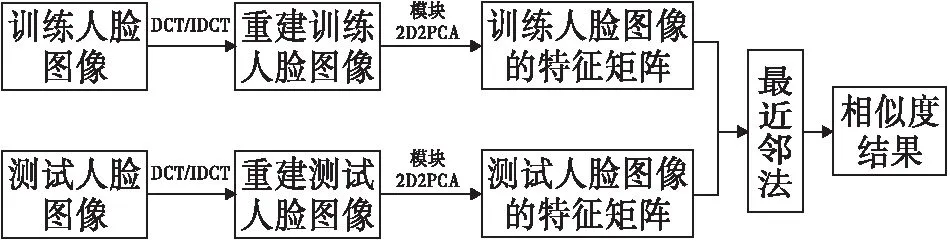
图3 本文流程图Fig.3 The flowchart

本文详细算法步骤如下：

(1)对每一张人脸图像进行DCT变换，将得到的DCT变换系数的左上角10个系数进行保留，并进行IDCT变换利用被保留的DCT变换系数，从而得到重建的人脸图像；

(2)对所有的训练样本图像进行步骤1的处理后，按照公式(10)和公式(11)得到列最优投影矩阵U和行的最优矩阵V，再根据公式(14)得到训练样本图像的特征矩阵；

(3)输入一个测试样本图像，按上述步骤1的方法对测试样本图像进行DCT和IDCT变换，按上述步骤2将重建后的测试样本图像矩阵投影到最优特征向量U和最优特征向量V上，从而得到测试样本图像的特征矩阵；

(4)图像识别是对所得到的特征矩阵进一步分析的过程，用最近邻分类法求得相似度结果从而得到测试样本所属类别。

3 实验结果与分析

本文利用英国剑桥Olivetti实验室的ORL人脸图像数据库，目前被广泛使用的。在这个人脸图像数据库中拍摄了不同的年龄、不同性别和不同种族的人，其中每个人有10幅人脸图像并且是灰度图像，尺寸大小为92×112.其中，人脸图像数据库中的人脸部分有表情和细节的变化，例如表情的变化、眼睛的眼或闭、是否戴眼镜等。

本实验利用ORL人脸图像数据库中的图片在MATLAB中进行了多次测试与对比，将本文算法与DCT和(2D)2PCA结合的算法进行了对比，运用后者算法的实验结果如图3(a)与(b)，有效果图可得图3(b)中相似度虽然很高但出现了误判，出现此结果是由于后者算法中提取的特征信息不完整，识别性能不稳定且鲁棒性差。

图4 DCT+(2D)2PCAFig.4 DCT+(2D)2PCA

而运用本文算法提取的人脸特征信息比较完整且有相当好的稳定性，如图4(a)与(b)，得到的都是正确的识别结果，是本文算法对不同对象的识别效果图。

图5 本文算法(DCT+分块(2D)2PCA)Fig.5 Algorithm of the paper(DCT+ Modular 2D2PCA)

再直接用分块(2D)2PCA的算法进行识别，结果如图5得到的不同对象的识别结果图。与本文算法图4的识别相似度相比，显然，本文算法的识别相似度更高。更能准确的识别正确的人脸图像。

图6 分块(2D)2PCAFig.6 Modular 2D2PCA

实验中选择ORL人脸图像库中的208张图片进行训练，人脸图像库中的其他图片作为测试集图片表1分别列出了上述三种算法的训练时间和每张图片的平均识别时间。表2列出了所用的三种不同算法的识别率与识别正确率。

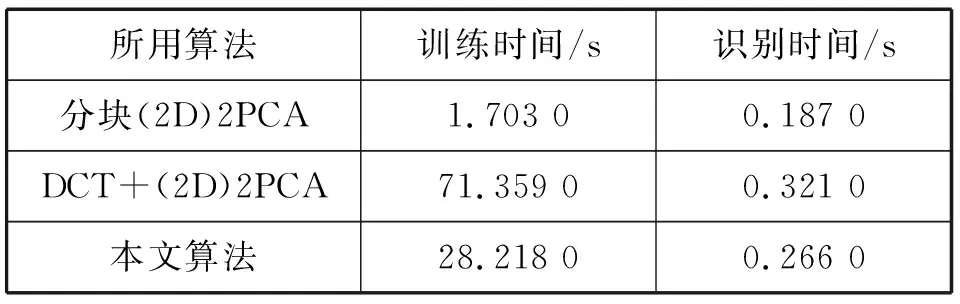
表1 三种不同算法的训练时间和识别时间Tab.1 Training time and recognition time of threedifferent algorithms

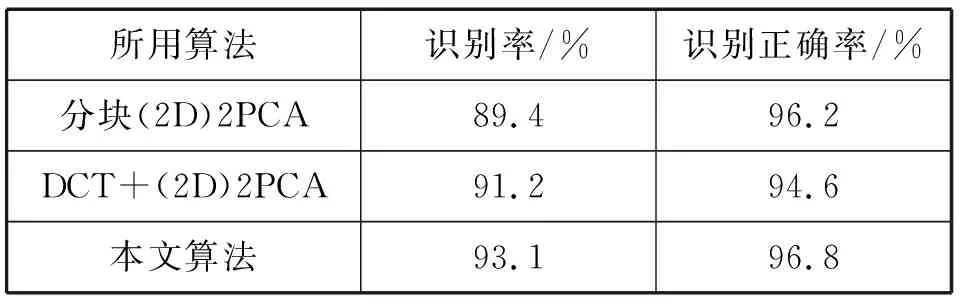
表2 三种不同算法的识别率与识别正确率Tab.2 Recognition rate and correct recognition rateof three different algorithms

实验结果表明，文中算法的训练时间相对较少，识别率和识别正确率相对较高，鲁棒性较强，识别时间相对较少，更适用在实际应用的人脸图像识别中。

4 结论

算法中首先应用二维离散余弦变换(DCT)对图像进行压缩并重建。能更好地利用了人脸的特征信息。然后应用分块(2D)2PCA的人脸特征提取算法，该算法既考虑了人脸图像矩阵的行方向与列方向各自的相关性，又有较小的维度。经过实验表明，本文算法用的特征向量维数较低，识别速率加快，识别的鲁棒性明显增强。在实际应用过程中能有效稳定性并提高了系统的性能指标。

参考文献：

[1] 姜文涛，刘万军，袁姮.一种基于曲量场空间的人脸识别算法[J].计算机学报，2012，35(8)：1739-1750.

[2] ZHAO W，CHELLAPPA R，ROSENFELD A，et al.Face recognition：a literature survey，CART-TR-948[R].Maryland：University of Maryland，2000.

[3] 张有为，甘俊英.人机自然交互[M].北京：国防工业出版社，2004.

[4] VEZZETTI E1，MOOS S，MARCOLIN F，et al.A pose-independent method for 3D face landmark formalization[J].Computer Methods and Programs in Biomedicine，2012，108(3)：1078-1096.

[5] ADAMS H，STEFFENS J，KIYOHARA K，et al.Method and apparatus to incorporate automatic face recognition in digital image collections：U.S.Patent 8，358，811[P].2013-1-22.

[6] CHAN C H，TAHIR M A，KITTLER J，et al.Multiscale local phase quantization for robust component-based face recognition using kernel fusion of multiple descriptors[J].Pattern Analysis and Machine Intelligence，IEEE Transactions on，2013，35(5)：1164-1177.

[7] 刘茜，荆晓远，姚永芳，等.基于统计正交性分析的彩色人脸识别[J].南京邮电大学学报：自然科学版，2013，33(1)：74-78.

[8] CHEN W L，ER M J，WU S Q.PCA and LDA in DCT domain[J].Pattern Recognition Letters，2005，26(15)：2474-2482.

[9] JADHAV D V，HOLAMBE R S.Rotation，illumination invariant polynomial kernel fisher discriminate analysis using radon and discrete cosine transforms based features for face recognition[J].Pattern Recognition Letters，2010，31(9)：1002-1009.

[10] 张娜娜，吴翔，马燕.DCT系数重组在特征脸中的应用研究[J].计算机工程与应用，2011，47(19)：197-199.

[11] TURK M，PETLAND A.Eigenfaces of Recognition[J].Cognitive Neuroscience，1991，3(1)：71-86.

[12] Zhang D，Zhou Z H，Chen S.Diagonal principal component analysis for face recognition[J].Pattern Recognition，2006，39(1)：140-142.

[13] 杨军，袁红照.结合小波变换和图像主元分析的人脸识别[J].计算机工程与应用，2010，46(4)：1-3.

[14] 廖正湘，陈元枝，李强.融合2DDCT、2DPCA和2DLDA的人脸识别方法[J].计算机应用与软件，2012，29(9)：237-239.

[15] 李文举，尉秀芹，高连军.基于分块2DDCT和(2D)2PCA的人脸识别[J].辽宁师范大学学报：自然科学版，2013，36(2)：174-177.

[16] QI Y F，ZHANG J S.(2D)2PCA LDA：An efficient approach for face recognition[J].Applied Mathematics and Computation，2009，213(1)：1-7.

[17] ZHANG D，ZHOU Z H.(2D)PCA：two-directional two dimensional PCA for efficient face representation[J].Neurocomputing，2008，69(1-3)：224-231.

[18] 王玉德，张学志.一种基于图像分块加权的(2D)2PCA人脸特征提取方法[J].激光杂志，2013，34(5)：25-27.