关于4×4分块矩阵的逆矩阵*
王静民,王利广
(①上海大学经济学院,200444,上海市;②曲阜师范大学数学科学学院,273165,山东省曲阜市)
在求较高阶数的矩阵的逆矩阵时,常常对其按照某种规则进行分块,化为一定阶数的分块矩阵[1-9].对矩阵分块是一种非常有效的技巧,使用分块矩阵不仅使表达简洁,而且常常通过把高阶矩阵的运算化为低阶矩阵的运算,可以将一些复杂而量大的计算转化为一系列简单而量小的计算来完成,从而大大简化计算量.同时,若分块恰当,使之出现较多的零矩阵或是单位矩阵等,会使计算得到大大的简化.因此如何求分块矩阵的逆矩阵,就变得非常重要.
文献[3-7]对一些特殊的2×2、3×3和4×4分块矩阵的逆的存在性进行了研究,文献[8]对2×2分块矩阵以及下三角分块矩阵的逆矩阵进行了研究,得到了一系列有意义的结果,但都是针对比较单一的情形.而事实上,当分块矩阵的其他子块可逆且满足一定关系时,矩阵仍有可能是可逆的且有具体的表达形式.在本文中,我们从其他子块来讨论了几类4×4阶分块矩阵的可逆性条件,并在可逆时给出了逆矩阵的表达式.
1 几类4×4分块矩阵的逆矩阵
在本节中,我们考虑几类4×4分块矩阵的可逆性条件,并在可逆时给出了逆矩阵的表达式.
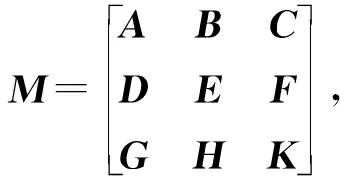
2 主要结果

证明因为

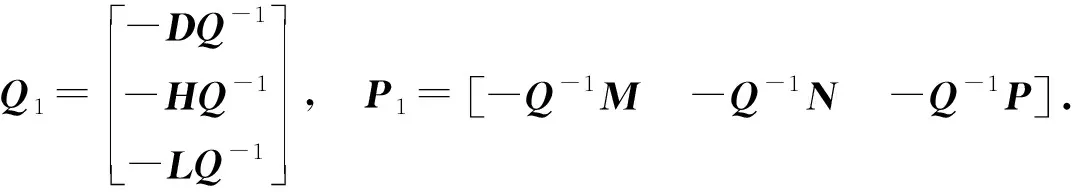
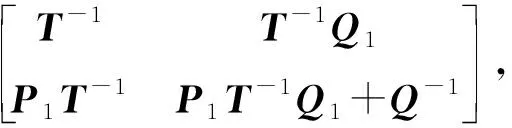


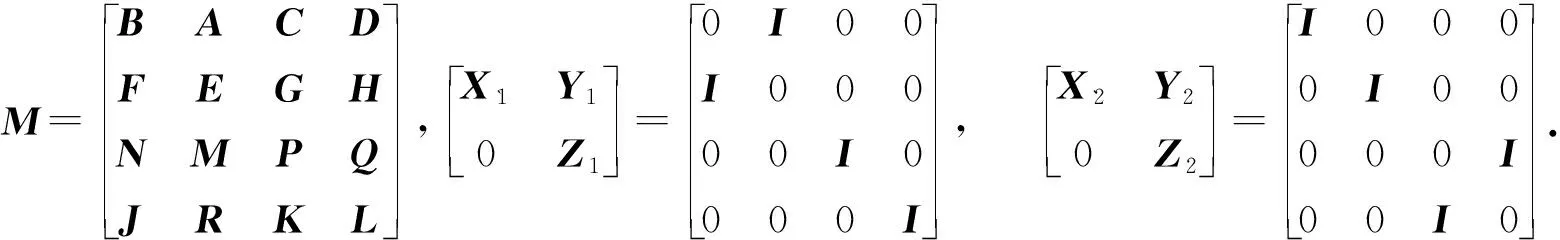

S可逆⟺R-KP-1M-(L-KP-1Q)(D-CP-1Q)-1(A-CP-1M)-[J-KP-1N-(L-KP-1Q)(D-CP-1Q)-1(B-CP-1N)][F-GP-1N-(H-GP-1Q)(D-CP-1Q)-1×(B-CP-1N)]-1[E-GP-1M-(H-GP-1Q)(D-CP-1Q)-1(A-CP-1M)],此时




S可逆⟺Q-NF-1H-(M-NF-1E)(A-BF-1E)-1(D-BF-1H)-[(P-NF-1G)-(M-NF-1E)(A-BF-1E)-1(C-BF-1G)][K-JF-1G-(R-JF-1E)(A-BF-1E)-1×(C-BF-1G)]-1[(L-JF-1H)-(R-JF-1E)(A-BF-1E)-1(D-BF-1H)]可逆,且
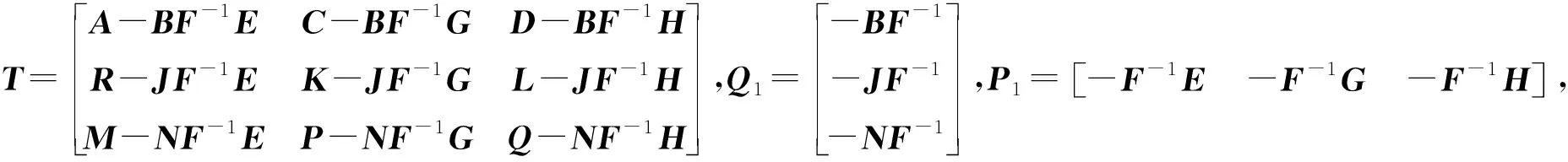
本节中只给出3个定理和3个推论,A、B、C、D、G、H、R、K、L、N可逆的情形可以通过矩阵变换转化成上述的定理和推理,从而求出矩阵的逆.

