基于模糊控制的九桥全地面起重机转向特性

马玉贤，刘中英，贾志绚

(太原科技大学，太原 030024)

九桥全地面起重机具有车身长、吨位大、轴数多等特点，且随着轴数的增加，车长越长，车辆转向难度增加，转向控制越发复杂，对其转向性能要求更高，研究难度也大大增加。目前，国内外对多桥转向技术的研究多在三桥～七桥之间进行[1-4]，对九桥车辆转向研究的文献较少，核心敏感技术都在国外大公司保护中无法获得，因此对九桥转向技术进行研究具有非常重要的理论意义及工程意义。

本文以某九桥全地面起重机转向系统为研究对象，利用MATLAB/Simulink工具箱建立车辆模型，MATLAB/Fuzzy工具箱设计模糊控制器，在模型中进行必要的参数设置，对其转向特性进行仿真分析。

图1 模糊控制原理图Fig.1 Schematic diagram of fuzzy control

1 多桥转向模糊控制器的设计

以九桥全地面起重机全轮转向为例，根据前桥车轮转角和车速来设计模糊控制器，前桥车轮转角通过驾驶者转动方向盘来控制，后八桥车轮转角可以根据一定的控制算法得到，使车辆可以顺利的完成转向，如图1所示。

1.1 设计模糊控制器的结构

车辆模糊控制器有两个输入和八个输出变量；输入量为车速与前桥车轮转角，输出语言变量分别为第二桥车轮转角、第三桥车轮转角、第四桥车轮转角、第五桥车轮转角、第六桥车轮转角、第七桥车轮转角、第八桥车轮转角和第九桥车轮转角。模糊控制器通过车辆的车速和前桥车轮转角实现对后八桥车轮转角的控制。

1.2 确定输入输出语言变量的隶属函数

首先确定控制变量，模糊分割控制器的输入、输出变量空间[5]。为使输出的精度更高，把前桥车轮转角、速度和后桥车轮转角空间划分为九个模糊集合，分别用NZ表示负最大、NB表示负很大、NM表示负中、NS表示负很小、Z0表示中间、PS表示正很小、PM表示正中、PB表示正很大、PZ表示正最大；在隶属函数编辑器中编辑隶属函数如图2-图4所示。

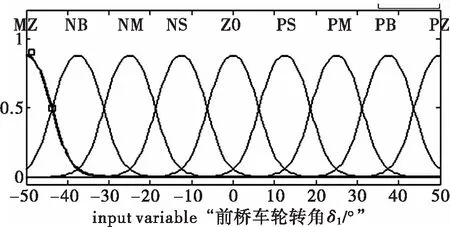
图2 前桥车轮转角隶属函数Fig.2 Subordinate function of front wheel steering angle

图3 车速隶属函数Fig.3 Subordinate function of vehicle speed

图4 后桥车轮转角隶属函数Fig.4 Subordinate function of rear wheel steering angle

1.3 建立模糊规则库

设计的模糊控制器是双输入多输出控制器，控制规则所遵循的原则是建立在对九桥全地面起重机转向特性研究的基础之上，文献[6]中已对九桥全地面起重机的转向特性、各桥转向关系、优化转向半径、全轮转向模式进行了研究。根据已有的结论编写模糊规则语言，建立模糊控制规则。

第二桥车轮转角为例的模糊规则：

第一桥车轮转角和速度都是负最大，第二桥车轮转角是负最大；

第一桥车轮转角是负很大，速度也是负最大，第二桥车轮转角是负很大；

第一桥车轮转角是负中，速度也是负最大，第二桥车轮转角是负中；

第一桥车轮转角是负很小，速度也是负最大，第二桥车轮转角是负很小；

第一桥车轮转角是中间，速度也是负最大，第二桥车轮转角是中间；

第一桥车轮转角是正很小，速度也是负最大，第二桥车轮转角是正很小；

第一桥车轮转角是正中，速度也是负最大，第二桥车轮转角是正中；

第一桥车轮转角是正很大，速度也是负最大，第二桥车轮转角是正很大；

……

规则库内的模糊语法为：

Ifδ1is NZ anduis NZ thenδ2is NZ；

Ifδ1is NB anduis NZ thenδ2is NB；

Ifδ1is NM anduis NZ thenδ2is NM；

Ifδ1is NS anduis NZ thenδ2is NS；

Ifδ1is Z0 anduis NZ thenδ2is Z0；

Ifδ1is PS anduis NZ thenδ2is PS；

Ifδ1is PM anduis NZ thenδ2is PM；

......

该模糊语言规则如表1所示。

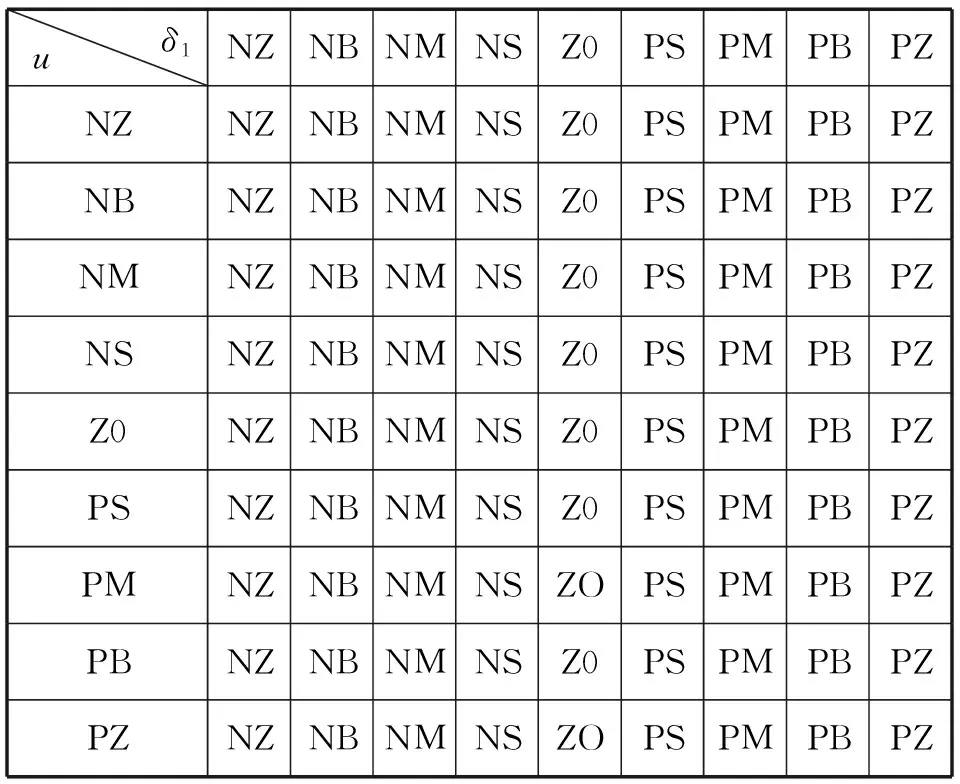
表1 输出第二桥车轮转角的模糊规则Tab.1 The fuzzy rules of the second axle steering angle

表1和表2为建立的第二桥车轮转角和第六桥车轮转角输出的模糊规则库。

同理，可建立其他各桥车轮转角模糊规则库。根据控制规则建立模糊控制器，可以通过模糊规则观察器和曲面观察器观测前后桥车轮转角与速度之间的关系，如图5所示。

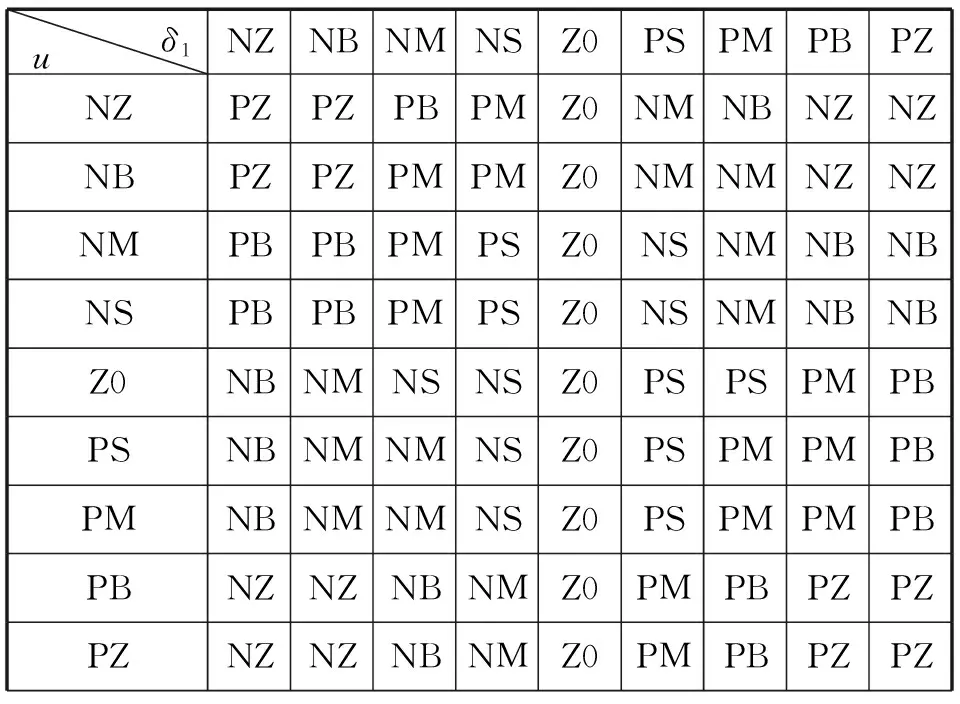
表2 输出第六桥车轮转角的模糊规则Tab.2 The fuzzy rules of the sixth axle steering angle

若发现输入和输出变量结果关系与文献[6]中分析结果出入太多，可及时在法则编辑器中修改，非常直观方便。由图5可知，设计的模糊控制器根据前桥车轮转角和车速对后桥车轮转角实施控制。当车速和前桥车轮转角增加时，第2-9转向桥车轮的转角值也随着变化。可以看到图5(a)-图5(d)中，随着前桥转角和车速的增加各后桥车轮转角也在增大，第2-5桥所有车轮转向与前桥车轮转向一致，而图5(e)-图5(h)中车辆第6-9各转向桥车轮与第1-5桥车轮在车速为高速时转向相同，低速时转向相反。与文献[6]中对九桥全地面起重机各转向桥的转角分析是一致的。

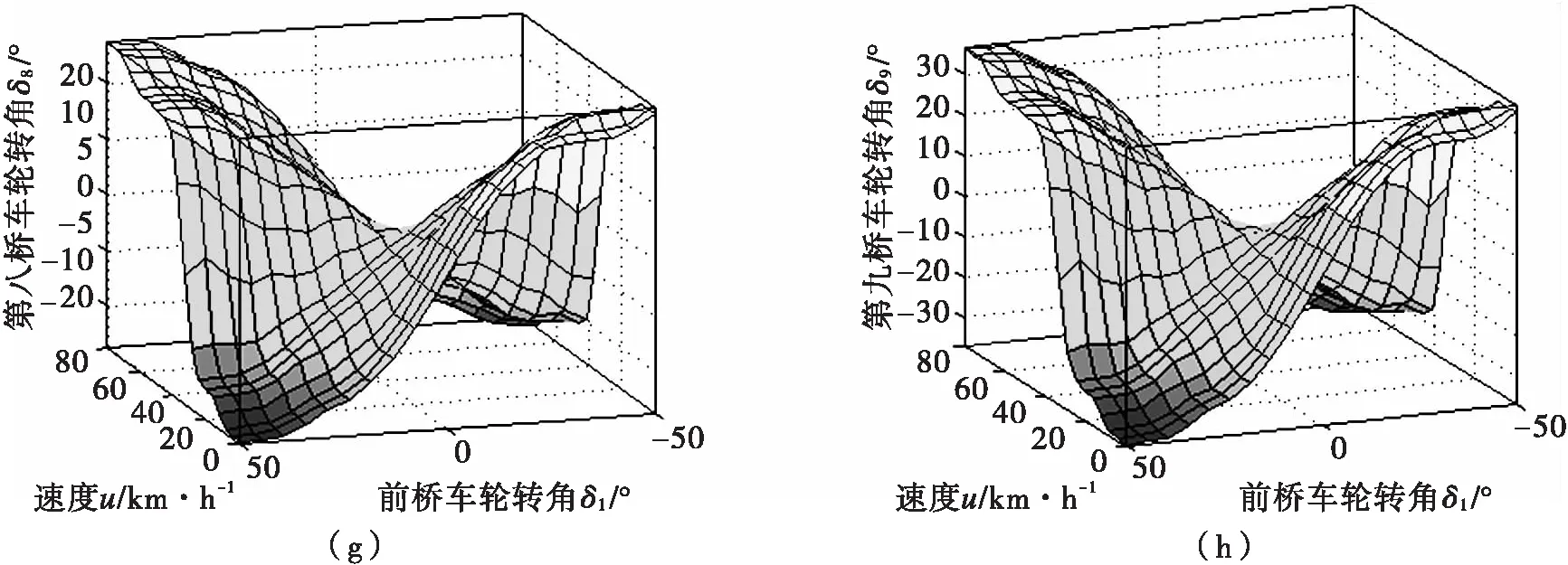
图5 前后桥车轮转角与速度的关系Fig.5 The relationship of for-and-aft wheel angle and speed

2 模糊控制系统仿真分析

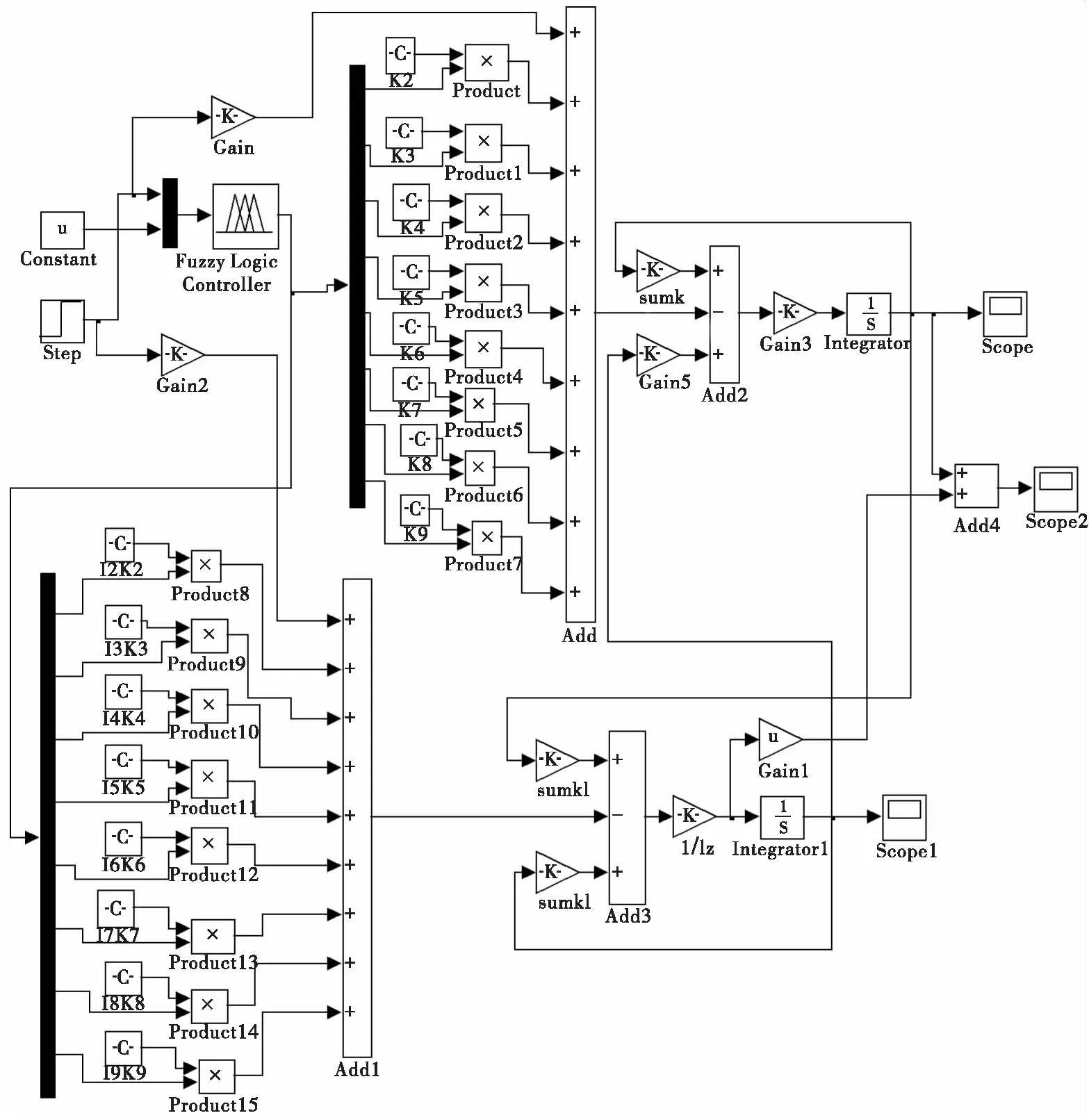
图6 多桥车辆模糊控制模型Fig.6 The model of fuzzy control with multi-axle vehicle

(1)

其中，m为车辆质量；u、v分别为质心速度V在x、y轴分量；Iz为车辆绕z轴转动惯量；li为第i桥距离车身质心长度；δi为第i桥车轮的转向角；ki为第i桥车轮的综合侧偏刚度；ωr为车辆绕z轴角速度；β为车辆质心处的侧偏角。

根据多桥车辆运动微分方程(1)式，采用图形建模方法，加入模糊控制器，建立模糊控制仿真模型，如图6所示。对车辆前桥车轮转角进行阶跃输入，仿真所用部分参数如表3所示，通过研究多桥车辆的侧偏角、横摆角速度及侧向加速度可以很好地反映车辆的动态性能。对于车辆模型和控制器均采用参数化输入，并得到多桥车辆侧偏角、横摆角速度和侧向加速度在不同速度下的关系曲线。

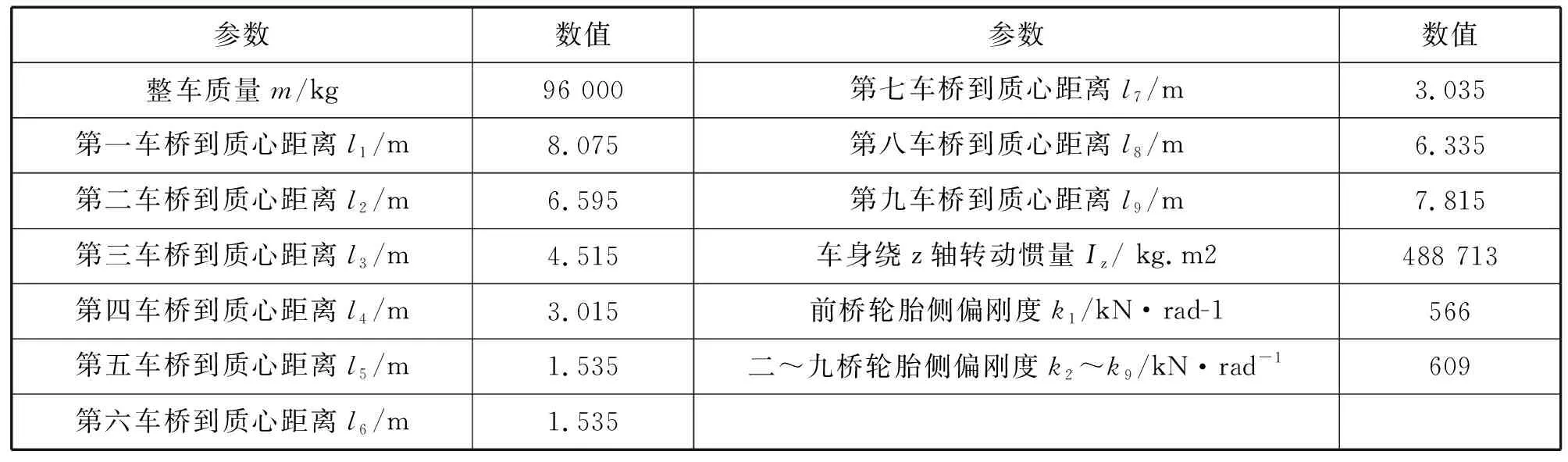
表3 某九桥全地面起重机多桥转向主要技术参数Tab.3 The main technical parameters of kiloton all-terrain-crane with multi-axle steering

通过多桥车辆模糊控制仿真分析，得到在不同车速工况下，多桥转向车辆质心侧偏角、横摆角速度和侧向加速度的阶跃响应随时间的变化曲线如图7～图9所示。

图7 桥转向车辆质心侧偏角阶跃响应曲线Fig.7 The step response curve of mass-center side-slipangle to multi-axle vehicle

由图7可知，质心侧偏角在0～3 s时振荡明显(超调量大)，但在3 s左右趋于稳定，质心侧偏角的超调量也随着增加。速度越高车辆质心侧偏角趋于稳定的时间越长，即质心侧偏角的稳态值趋于零的速度越慢。采用模糊控制可以很好地改善车辆在高速转向行驶时稳态值比较大、车辆质心侧偏角很难趋于零、车辆高速转向行驶不稳定的特点。这说明此控制方法可以很好地改善车辆多桥转向姿态。

由图8可知，速度在15～45 km/h时，随着速度的增加车辆横摆角速度稳态值逐渐增大；在45～75 km/h时，随着车速的增加车辆横摆角速度稳态值逐渐减小。随着时间的增加，速度越快车辆横摆角速度的趋于稳态值的调节时间越长。

图8 多桥转向车辆横摆角速度阶跃响应曲线Fig.8 The step response curve of the yaw rate withmulti-axle vehicle

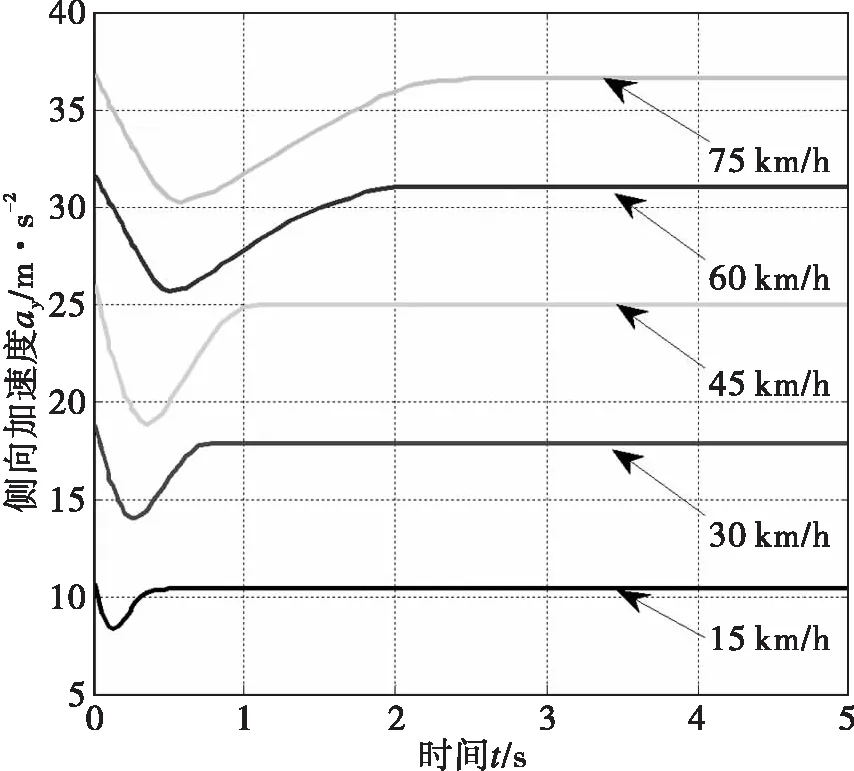
图9 侧向加速度阶跃响应曲线Fig.9 The step response curve of lateral acceleration

由图9可知，多桥车辆转向时，车速越高，车辆侧向加速度的调节时间越长，高速时，车辆侧向加速度的稳态值越大，速度越高超调量增加越快。侧向加速度越大，车辆行驶越不稳定。

3 结论

(1)为避免车辆在高速转向时发生侧滑失稳，针对九桥全地面起重机转向特性设计模糊控制器。仿真表明采用全轮转向模糊控制可使车辆的质心侧偏角在高速转向行驶时也能基本为零。随着时间的改变，横摆角速度和侧向加速度均能很快达到稳态值。

(2)多桥转向采用模糊控制，建模方便直观、容易实现，此控制方法可很好地控制车辆在低速时的转向灵活性，以及在高速时转向稳定性。

参考文献：

[1] 李华师，韩宝玲，罗庆生，等.基于模糊控制的三桥车辆全轮转向性能仿真[J].农业工程学报，2012，28(13)：34-41.

[2] WATANABE K，YAMAKAWA J，TANAKA M，et al.Turning characteristics of multi-axle vehicles[J].Journal of Terramechanics，2007，44(1)：81-87.

[3] 胡敏杰.全地面起重机多桥转向系统模糊PID控制研究[D].秦皇岛：燕山大学，2012.

[4] 周富家.多轮转向全地面起重机操纵稳定性控制算法研究[D].长春：吉林大学，2007.

[5] 陈杰.MATLAB宝典：第三版[M].北京：电子工业出版社，2011.

[6] 刘中英，贾志绚，李涵兵，等.千吨级全地面起重机转向特性研究[J].建筑机械，2014(2)：82-86.