折臂式随车起重机的动力学分析

张 帅，晋民杰，范 英，杨明星，马 俊，杨京山

(太原科技大学，太原 030024)

折臂式随车起重机是安装在载货汽车上的一种附加起重设备[1]。它主要由立柱、动臂、动臂油缸、两个四连杆机构、吊臂和吊臂油缸七部分组成[2](见图1)。其中动臂油缸、吊臂油缸和吊臂上的伸缩臂油缸为主动件，其他为从动件。

折臂式随车起重机的动力学分析是起重作业范围分析的基础，也是有限元分析及其结构优化的基础。由于构件的数量较多，直接列方程解其动力学方程较为困难，分析动力学规律就更难上加难了。

Creo软件集参数化建模技术、直接建模技术和三维可视化技术于一体[3]。本文用Creo软件对折臂式随车起重机建模和装配，并对特定工况进行动力学分析。此方法省去了复杂地动力学方程的建立和求解。国内外论文主要是应用Creo软件计算某一特定工况下整机的动力学，而本论文在动力学计算的基础上分析出了动臂油缸受力的偏微分方程组。

MATLAB软件简单易学，代码短小高效，计算功能全面[4]，计算偏微分方程组也非常方便。

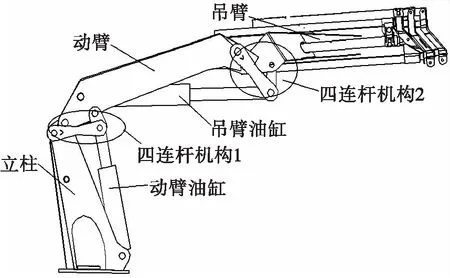
图1 折臂式随车起重机机构图Fig.1 Mechanism of folding-jib lorry loading crane

1 折臂式随车起重机Creo模型的建立

折臂式随车起重机Creo模型建立的方法如下：

(1)主要尺寸的确定。根据折臂式随车起重机的机构特点，确定主要尺寸，绘制运动简图如图2所示。

(2)细节尺寸的确定。细节特征需要采用参数化建模工具，参数化建模需要细化实际的工程特征，如拔模、加厚、倒角、倒圆角、孔的尺寸确定等，以确定各个构件的三维图。部分构件的三维图如图3所示。

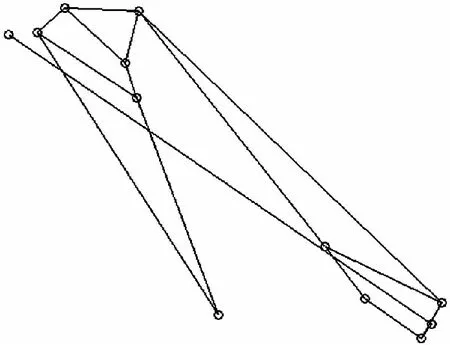
图2 机构运动简图Fig.2 Kinematic diagram of mechanism

图3 构件的三维图Fig.3 3D mechanism

(4)模型的装配。折臂式随车起重机装配时用到的约束类型有圆柱约束、销钉约束和滑动杆约束。其中各个约束对应的自由度见表1所示[5]。

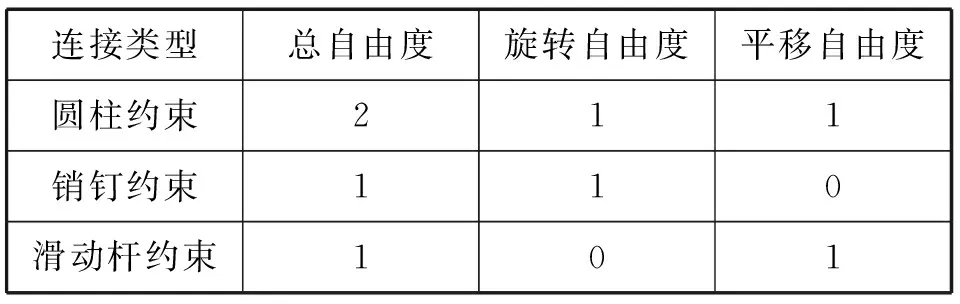
表1 各运动副与对应的自由度Tab.1 Kinematic pairs and their DOF

伸缩臂、伸缩油缸、动臂油缸和吊臂油缸用滑动杆约束连接。除此之外的构件被销钉约束或圆柱约束进行连接。四连杆机构中有且只有一个是圆柱约束，否则连四杆机构不是欠约束就是多一个虚约束。图4给出了折臂式随车起重机装配结果图。

图4 装配图Fig.4 Assembly drawing

(5)运动参数设置。伺服电动机添加主动件的约束上。按照计算出的油缸伸缩速度设置伺服电动机。油缸伸缩速度是由流量、油缸内径和油杆直径来确定。油缸伸长时速率见式(1)，油缸收缩时速率见式(2).

(1)

(2)

其中：Q为油缸流量；

D为油缸内径；

d为油杆直径。

虽然实际起吊的过程中液压缸的运行速率是变化的，非恒定的，但由于起重机运行速度较小，因此加速度和角加速度引起的惯性力也较小，则在模型的仿真过程中速率设为定值。

2 折臂式随车起重机工况分析

折臂式随车起重机的工况依起重幅度分为低幅度工况和中高幅度工况两种。

低幅度工况下伸缩臂不伸出。起重机的起升和变幅都是通过动臂油缸和吊臂油缸相互配合而实现的。由于动臂油缸的受力一般都会高于吊臂油缸，所以一般动臂油缸静止，吊臂油缸动作以完成起升和变幅。

中高幅度工况下伸缩臂伸出。此工况下吊臂油缸维持全部伸出的状态，动臂油缸和伸缩臂油缸配合使用来完成起吊作业。

3 折臂式随车起重机动力学分析总揽

把图1所示的各个构件进行编号，得到如图5所示的编号图。

图5 编号图Fig.5 Numbered figure

应用Creo的动态分析可以测得某工况下各个构件的受力情况，把各个构件的受力曲线都综合到一张曲线图里，就形成了如图6所示的某工况下起重机受力分析总揽图。

图6 受力分析总揽Fig.6 Force analysis diagram

由图6可知动臂油缸受力最大。又对其他工况进行动力学分析，分析结果均是动臂油缸受力一直维持最大。因此下文中主要对动臂油缸的受力进行分析。

4 折臂式随车起重机动力学仿真

经过对模型的动力学仿真，总结出动臂油缸的受力过程可分为三个阶段。这三个阶段的受力变化如图7～图9所示。

如图7所示，第一阶段动臂油缸受力变化曲线有如下特点：(1)随着吊臂油缸伸长，曲线左端点纵坐标值增大，右端点以及曲线驻点的纵坐标值减小；(2)吊臂油缸伸长时间小于4.4 s，动臂油缸伸长的长度受到限制；(3)吊臂油缸伸长时间大于等于4.4 s时，动臂油缸可以全程运动。

图7 第一阶段动臂油缸压力变化曲线Fig.7 Pressure variation curve of movable arm oilcylinder in the firse stage

如图8所示，第二阶段动臂油缸压力变化曲线有如下特点：(1)随着吊臂油缸长度变大，曲线左端点以及第一个驻点的纵坐标值变大，右端点以及第二个驻点的纵坐标值变小；(2)此阶段动臂油缸可以全程运动。

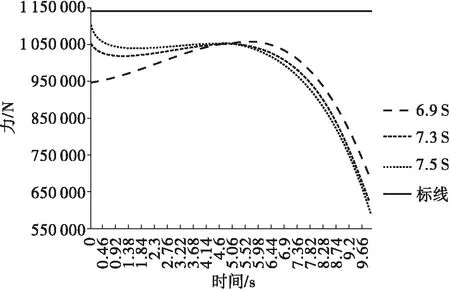
图8 第二阶段动臂油缸压力变化曲线Fig.8 Pressure variation curve of movable arm oilcylinder in the second stage

如图9所示，第三阶段动臂油缸压力变化曲线有如下特点：(1)随着吊臂油缸长度变大，曲线左端点以及第一个驻点的纵坐标值变大，右端点以及第二个驻点的纵坐标值变小；(2)吊臂油缸伸长时间大于7.64 s时，动臂油缸伸长的长度受到限制；(3)吊臂油缸伸长时间小于7.64 s时，动臂油缸可以全程运动。

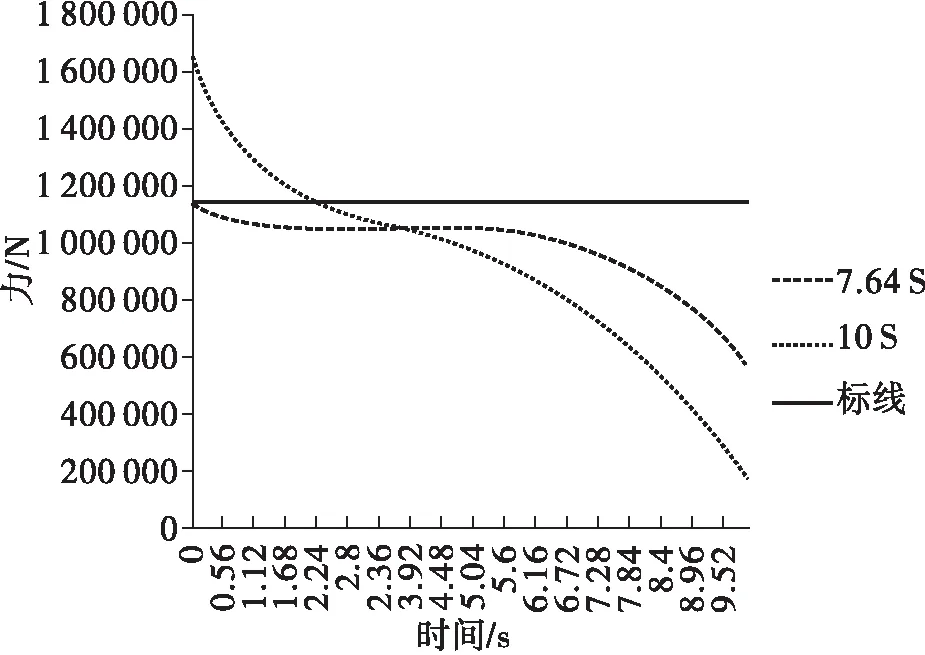
图9 第三阶段动臂油缸压力变化曲线Fig.9 Pressure variation curve of movable armoil cylinder in the third stage

动臂油缸受力情况变成如图9所示的第三阶段后幅度再大曲线的形状也不会改变了，即曲线呈现先高后低的现象且前半曲线是向上凹的，后半曲线是向下凹的，中间有一个拐点(曲线二阶导数为0的点)。所以为保证动臂油缸有较大的举升能力，中高幅度作业时应使伸缩臂轴线与水平面夹角为正。

5 折臂式随车起重机动力学分析

5.1 起重量对动臂油缸受力的影响

下面以同一运行工况而不同的起重量来讨论起重量对动臂油缸的受力的影响。同一运动工况下，起重量分别是3 t、4 t或5 t时动臂油缸的受力曲线如图10所示。

图10 重量对受力的影响Fig.10 The influence of weight to force

如图10的曲线可知动臂油缸的压力随起重量的增加而增加。由曲线的数据可知只要起重量的增量是相同的，动臂油缸压力的增量也相同。即设起重量为3 t时动臂油缸受力矩阵为X，起重量为4 t时动臂油缸受力矩阵为Y，起重量为5 t时动臂油缸受力矩阵为Z，则X、Y和Z满足式(3).

Y-X=Z-Y

(3)

将式(3)所给的公式写成微元法的形式如式(4)所示。

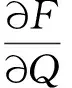
(4)

其中：F为动臂油缸所受压力；

Q为起重量；

C为常数向量。

5.2 伸缩臂长度对动臂油缸受力的影响

下面以同一运行工况而不同的伸缩臂伸长长度来讨论起伸缩臂伸长长度对动臂油缸的受力的影响。图11给出了同一运动工况和起重量时，伸缩臂长度分别是0 mm、500 mm、1 000 mm和1 500 mm的情况下动臂油缸所受的压力曲线。

图11 伸缩臂长度对受力的影响Fig.11 The influence of jib length on force

如图11所示给出的曲线图可以看出，随着伸缩臂伸出长度的增加，动臂油缸的受力也是随之增加的。设伸缩臂长度为0 mm时动臂油缸受力矩阵为K，伸缩臂长度为500 mm时动臂油缸受力矩阵为L，伸缩臂长度为1 000 mm时动臂油缸受力矩阵为M，伸缩臂长度为1 500 mm时动臂油缸受力矩阵为N.L-K，M-L，N-M的数据有与5.1节所述的X、Y和Z有着共同的规律。即其满足式(5).

(M-L)-(L-K)=(N-M)-(M-L)

(5)

将(5)所给的公式写成微元法的形式如式(6)所示。

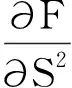
(6)

其中：F为动臂油缸所受压力；

S为伸缩臂伸长长度；

D为常数向量。

5.3 伸缩速度对动臂油缸受力的影响

动臂油缸的伸缩速度对动臂油缸的受力大小的影响微乎其微，实际计算中可以忽略不计。即其满足式(7)所示的规律。

(7)

其中：F为动臂油缸所受压力；

V为动臂油缸伸缩速度。

6 折臂式随车起重机动力学方程的求解

由式(3)、式(6)-式(7)所组成的偏微分方程组解得动臂油缸受力式如(8)所示[6]。

F=CQ+D1D2+D2S+E

(8)

其中：F为动臂油缸所受压力；

Q为起吊重量；

S为伸缩臂伸长长度；

C、D1、D2和E为常数向量。

根据Creo中所测数据导入到Excel中，并通过Exclink将Excel中的数据导入到MATLAB中，应用MATLAB的矩阵运算计算出常数C、D1、D2和E，即可完成动臂油缸受力公式的求解。

7 结论

(1)折臂式随车起重机动臂油缸受力最大，应作为动力学分析的主要研究对象。

(2)动臂油缸的受力随着幅度从小到大先后经历三种曲线变化趋势。

(3)起重量、幅度和起升速度分别与动臂油缸受力之间存在偏微分关系。

参考文献：

[1] 杨路.随车起重运输车臂架设计要素[J].商用汽车，2012 (8)：56-59.

[2] 刑玉生，刘佃富.折臂式随车起重机的变幅机构[J].起重运输机械，1998(11)：7-9.

[3] 李素云.基于Pro/e端盖注射模参数化设计[J].贺州学院学报，2009 (3)：136-138.

[4] 陈杰.MATLAB宝典[M].北京：电子工业出版社，2009.

[5] 佟河亭，李超，王炳强.Pro/ENGINEER Wildfire 4.0机构运动仿真与动力学分析[M].北京：人民邮电出版社，2010.

[6] 李斌.塔式起重机起重特性分析[J].沈阳建筑工程学院学报，1991(3)：242-246.

[7] TAYLOR M E.Partial Differential EquationsⅡ[M].Beijing：World Book Inc，2014.