交换超立方体在PMC模型下的g好邻条件诊断度
刘秀丽,原 军,马 雪
(太原科技大学应用科学学院,太原 030024)
随着并行计算机系统规模的逐步扩大,系统中元件出现故障的可能性大大增加。为了保持并行计算机系统的可靠性,系统中的故障元素应该被及时诊断出来并被替换。Preparata等[1]在1967年将图论方法应用于计算机系统的故障诊断,创建了系统级故障诊断理论。PMC模型是他们首次提出的系统故障诊断模型。诊断度是系统级故障诊断研究的一个重要的参数,它是多处理器系统能够诊断的最大故障处理器的个数。传统的诊断度总是假定系统的任何部分都可能同时失灵,但是对于大规模并行计算机系统而言,每一个处理器所有相邻的处理器同时发生故障的概率是非常小的,因此它远远低估了并行计算机系统的自我诊断能力。为了克服这个缺陷,2005年Lai等[2]通过限制每个顶点的所有邻点不能同时发生故障,提出了一个新的诊断测度,称为条件诊断度。在此概念的启发下,2012年Peng等[3]通过限制每个非故障顶点都有g个非故障邻点,提出了g好邻条件诊断度。同时,在文献[3]中,Peng等给出了超立方体在PMC模型下的g好邻条件诊断度。本文研究了交换超立方体在PMC模型下的g好邻条件诊断度,并由此推出对偶立方体在PMC模型下的g好邻条件诊断度。
1 预备工作
设G=(V,E)是一个无向图,其中V=V(G),E=E(G)分别表示图G的顶点集和边集。当用图来表示并行计算机系统时,顶点代表处理器,边代表处理器之间的连接。假设V′是V的一个非空子集,以V′为顶点集,以两端点均在V′中的边的全体为边集所组成的子图,称为G的由V′导出的子图,记为G[V′];G[V′]称为G的导出子图。G的顶点v的度dG(v)是指G中与v关联的边的数目,用δ(G)和△(G)来表示G的顶点的最小度和最大度。对于图G的任一顶点集S,定义G中S的邻集为与S的顶点相邻的所有顶点的集,记为NG(S).定义CG(S)=NG(S)∪V(S).设F为G的任意顶点子集,若V-F在中任意一点v在导出子图G[V-F]中至少有g个邻点,则称F为G的g好邻条件故障集。如果G-F不连通且G-F的每个连通分支满足最小度为g,则称F是一个g好邻条件故障割。G的所有g好邻条件故障割的最小顶点数称为G的g好邻条件连通度,记为κ(g)(G).其它文中未予定义直接使用的符号和术语参见文献[4].
在PMC模型下,相邻的两个处理器可以相互进行测试,对于图G中的任意一条边(u,v)∈E(G),顶点对(u,v)代表从u到v的测试,称u为测试者,v为被测试者。我们用1(0)代表测试结果是否发生故障,用σ(u,v)表示测试结果。当u是故障的,结果是不可靠的,σ(u,v)可能是0或1.但当u是非故障的,若v是故障的,则σ(u,v)为0,若v是非故障的,则σ(u,v)为1.所有测试结果的集合称为系统G的校验子,记作σ.它可以用一个有向图T=(V(G),L)表示,其中(u,v)∈L表示u和v在图G中相邻。对于一个给定的校验子σ,如果σ产生的条件是:存在顶点子集F⊆V,对于任意一条边(u,v)∈L,并且σ(u,v)=1当且仅当v∈F,则称故障集F与校验子σ是一致的。对两个不同的顶点子集F1和F2,若σ(F1)∩σ(F2)=φ,则称F1和F2是可区分的,(F1,F2)为可区分的点对;否则,称F1和F2是不可区分的,(F1,F2)为不可区分的点对。
对于给定的校验子σ,若系统G中发生故障的处理器的数目不超过t时,所有的处理器都能被准确地判断出是否发生故障,则称G是t-可诊断的。使得G是t-可诊断的t的最大值称为G的诊断度,记为t(G).
定理1设F1和F2是G中任意两个不同的顶点子集,且|F1|≤t,|F2|≤t.则G是t-可诊断的当且仅当F1和F2是可区分的。
2012年,Peng等在文献[3]中提出了g好邻条件诊断度的概念。
定义2若G中任意两个顶点数至多为t的g好邻条件故障集F1,F2都是可区分的,则称G是g好邻条件t-可诊断的。使得G是g好邻条件t-可诊断的最大值t称为G的g好邻条件诊断度,记作tg(G).
本文研究的是交换超立方体。作为超立方体的一种变形网络,它是由超立方体Qs+t+1去掉一些边得到的。它不仅保留了超立方体许多有用的性质,而且降低了互连网络的复杂性。下面给出交换超立方体的概念和性质。
给定一个正整数,称序列xnxn-1…x1为有序n元组。对任一个有序n+1元组unun-1…u1u0,称ur为它的r维,其中0≤r≤n.记In={1,2,…,n}.
定义3设整数t≥1,s≥1,交换超立方体EH(s,t)为无向图,顶点集V(EH(s,t))={us+t…ut+1ut…u1u0|u0,ui∈{0,1},i∈Is+t},两顶点u=us+t…ut+1ut…u1u0和v=vs+t…vt+1vt…v1v0相邻当且仅当满足以下三个条件:
(1)u和v在r维恰有一个坐标不同,其中0≤r≤s+t;
(2)若r∈I,则u0=v0=1;
(3)若r∈Is+t-It,则u0=v0=0.
称这样的边(u,v)为r维边。交换超立方体EH(1,1)和EH(1,2)如图1所示。

图1 交换超立方体EH(1,1)和EH(1,2)Fig.1 Two exchanged hypercubes EH(1,1) and EH(1,2)
由定义3可知EH(s,t)有2s+t+1个顶点和(s+t+2)2s+t-1条边,且它是由超立方体Qs+t+1去掉一些边得到的,即当0维为0时,对r∈It,去掉所有的r维边;当0维为1时,对r∈Is+t-It,去掉所有的r维边。因此,EH(s,t)是最小度δ(EH(s,t))=min{s,t}+1和最大度△(EH(s,t))=max{s,t}+1的二部图。当s=t=1时,EH(s,t)是长为8的圈。当s=t≥2时,EH(s,t)退化为新近研究较多的对偶立方体DCn[6-7].
引理4[8]EH(s,t)同构于EH(t,s).


引理6[5]设1≤s≤t,0≤g≤s,则κg(EH(s,t))=2g(s+1-g).
引理7设H是EH(s,t)的连通子图,且δ(H)≥g,0≤g≤s,则|V(H)|≥2g.
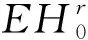
2 主要结果
对称差F1△F2=(F1-F2)∪(F2-F1).DahBura等[5]给出了判定在PMC模型下,F1和F2是否可区分的充要条件。
定理8[9]设F1和F2是G中任意两个不同的顶点子集,则F1和F2是可区分的当且仅当存在一个顶点u∈V-(F1∪F2),x∈F1△F2,使得(u,v)∈E.如图2所示。
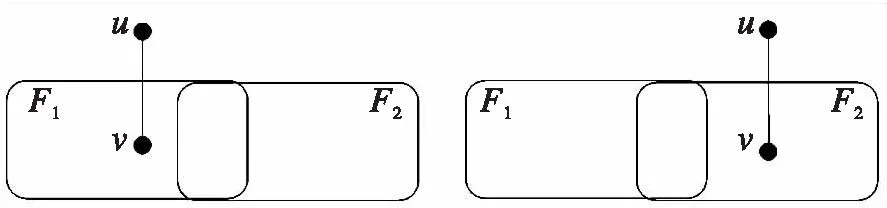
图2 在PMC模型下的可区分点集对(F1,F2)Fig.2 A distinguishable pair(F1,F2)of PMC model
首先讨论tg(EH(s,t))的上界。
定理9设0≤g≤s,则tg(EH(s,t))≤2g(s+2-g)-1.
证明:令X={xg0s+t+1-g|x∈(0,1)}.由定义3知,导出子图EH(s,t)[X]是一个g维超立方体Qg,且NEH(s,t)(X)={xg0p10s-p-g-10t+1|0≤p≤s-g-1,g≤s-1}∪{xg0s+t-g1},其中x∈{0,1}.对任一顶点v∈X,有dEH(s,t)(v)=s+1,且v在X中有g个邻点,因此v在NEH(s,t)(X)中有s+1-g个邻点。同时,由X的取法与定义3可知,NEH(s,t)(X)中每一个顶点在X中有且仅有一个邻点,因此|NEH(s,t)(X)|=2g(s+1-g).令F1=NEH(s,t)(X),F2=CEH(s,t)(X),故|F1|=2g(s+1-g),|F2|=2g(s+2-g).因为X=F1△F2,NEH(s,t)(X)=F1,如图3所示,所以由定理8可知,F1和F2是不可区分的。
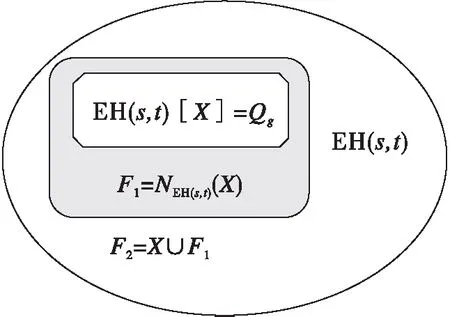
图3 顶点集F1和F2Fig.3 Vertex set of F1 and F2
令Y=V(EH(s,t))-(F1∪F2).要证F1和F2是g好邻条件故障集,只需证明EH(s,t)[X]和EH(s,t)[Y]满足最小度至少为g.因为导出子图EH(s,t)[X]是一个g维超立方体Qg,所以EH(s,t)[X]满足最小度至少为g.现在考虑EH(s,t)[Y]中的顶点。令v∈Y,若v与NEH(s,t)(X)中的顶点相邻,则v有如下三种形式:
形式1:v=xg0p10s-p-g-10t1,其中0≤p≤s-g-1;g≤s-1;
形式2:v=xg0s-g0r10t-r-11,其中0≤r≤t-1;
形式3:v=xg0p10q10s-p-q-g-20t+1,其中0≤p≤s-g-2,0≤q≤s-g-2.
如果v满足前两种形式,那么v在NEH(s,t)(X)中有一个邻点,因此v在Y中至少有s个邻点,且s≥g;如果v满足最后一种形式,那么s-g≥2,且v在NEH(s,t)(X)中含有两个邻点,因此v在Y中至少有s-1个邻点,且s-1≥g.由v的任意性可知EH(s,t)[V]满足最小度至少为g.因此,F1和F2是EH(s,t)的g好邻条件故障集。
由于F1和F2是不可区分的,且|F1|=2g(s+1-g),|F2|=2g(s+2-g),故由定理1和定义2可知当0≤g≤s时,EH(s,t)的g好邻条件诊断度tg(EH(s,t))≤2g(s+2-g)-1.证毕。
下面将讨论tg(EH(s,t))的下界。
定理10设0≤g≤s,则tg(EH(s,t))≥2g(s+2-g)-1.
证明:由定义2可知,只需证明EH(s,t)是g好邻条件2g(s+2-g)-1诊断的。要证EH(s,t)是g好邻条件2g(s+2-g)-1诊断的,只需证明在EH(s,t)中任意两个顶点数至多为2g(s+2-g)的g好邻条件故障集F1,F2都是可区分的。
假设存在两个满足条件的g好邻条件故障集F1和F2是不可区分的。由定理8可知,F1和F2不可区分有两种情况:V(EH(s,t))=F1∪F2或者V(EH(s,t))≠F1∪F2且V(EH(s,t))-(F1∪F2)与F1△F2之间没有边。不失一般性,假设F2-F1≠φ.
情况1:V(EH(s,t))=F1∪F2.
因为s≥g,t≥1且EH(s,t)的所有点都在F1∪F2中,所以:
2s+t+1=V(EH(s,t))=|F1|+|F2|-|F1∩F2|≤2(2g(s+2-g)-1)≤4×2s-2<2s+2≤2s+t+1,矛盾。
情况2:V(EH(s,t))≠F1∪F2,且V(EH(s,t))-(F1∪F2)与F1△F2之间没有边。
因为F2-F1≠φ,F1为g好邻条件故障集,且δ(EH(s,t)[F1-F2])≥g.由引理7可知,|F2-F1|≥2g.
断言:F1∩F2是EH(s,t)的g好邻条件故障割。
首先,假设F1⊂F2.因为F2是EH(s,t)的g好邻条件故障集,所以δ(EH(s,t)-F2)≥g.又因为δ(EH(s,t)[F1-F2])≥g,所以F1∩F2为EH(s,t)的g好邻条件故障集。由于V(EH(s,t))-(F1∪F2)与F1△F2之间没有边,故V(EH(s,t))-F2与F2-F1不连通。因此当F1⊂F2时,F1∩F2是EH(s,t)的g好邻条件故障割。
现在假设F1⊄F2,即F2-F1≠φ,且F1-F2≠φ.因为F1和F2都是g好邻条件故障集,且V(EH(s,t))-(F1∪F2)与F1△F2之间没有边,所以δ(EH(s,t)[F1-F2])≥g,δ(EH(s,t)[F2-F1])≥g,且δ(EH(s,t)-(F1∪F2))≥g.由此可知,F1∩F2是EH(s,t)的g好邻条件故障集。由于V(EH(s,t))-(F1∪F2)与F1△F2之间没有边,故V(EH(s,t))-(F1∪F2)与F1△F2不连通。因此当F1⊄F2时,F1∪F2是EH(s,t)的g好邻条件故障割。断言成立。
由引理6可知,κ(g)(EH(s,t))=2g(s+1-g).因为F1∩F2是EH(s,t)的g好邻条件故障割,所以|F1∩F2|≥2g(s+1-g).从而,|F2|=|F2-F1|+|F1∩F2|≥2g(s+2-g),与假设|F2|≤2g(s+2-g)-1矛盾。证毕。
结合定理9和定理10,我们可以得到当1≤s≤1,0≤g≤s时,在PMC模型下,交换超立方体的g好邻条件诊断度。
定理11设1≤s≤t,0≤g≤s,则交换超立方体EH(s,t)的g好邻条件诊断度tg(EH(s,t))=2g(s+2-g)-1.
对偶立方体DCn是超立方体的另一种变形网络。因为EH(n,n)≅DCn,所以可以得到下面的结论。
推论设n≥2,则对偶立方体DCn在PMC模型下的g好邻条件诊断度tg(DCn)=2g(n+2-g)-1.
参考文献:
[1] PRETARATA F P,METZE G,CHIEN R T.On the connection assignment problem of diagnosis systems[J].IEEE Transactions on Computers,1967,16(12):848-854.
[2] LAI P L,TAN J J M,CHANG C P,HSU L H.Conditional diagnosability measures for large multiprocessor systems[J].IEEE Transactions on Computers,2005,54:165-175.
[3] PENG S L,LIN C K,TAN J J M,HSU L H.The g-good-neighbor conditional diagnosability of hypercube under PMC model[J].Applied Mathematics and Computation,2012,218:10406-10412.
[4] BONDY J A,MURTY U S R.Graph Theory with Applications[M].New York:The Macmillan Press Ltd,1976.
[5] LI X J,XU J M.Generalized measures of fault tolerance in exchanged hypercubes[J].Information Processing Letters,2013,113:533-537.
[6] SHIH Y K,CHUANG H C,KAO S S.Mutually independent Hamiltonian cycles in dual-cubes[J].The Journal of Super computing,2010,54 (2):239-251.
[7] LI Y,PENG S,CHU W.Fault-tolerant cycle embedding in dual-cube with node faulty[J].International Journal of High Performance Computing and Networking,2005,3(1):45-53.
[8] LOH P K K,HSU W J,PAN Y.The exchanged hypercube[J].IEEE Transactions on Parallel and Distributed Systems,2005,16 (9):866-874.
[9] DAHBURA A T,MASSON G M.AnO(n2.5) faulty identification algorithm for diagnosable systems[J].IEEE Transactions on Computers,1984,33:486-492.

