提高架空输电线覆冰承载能力的研究

杨 昆，梁清香

(太原科技大学应用科学学院，太原 030024)

覆冰的影响在输电线路设计和运行中是必须考虑的因素，输电线路常常由于覆冰过厚而发生输电线拉断及输电塔倒塌事故。2008年初，低温雨雪冰冻天气覆盖我国南方、华中、华东地区，导致贵州、湖南、广东、云南、广西和江西等省输电线路大面积、长时间停运，造成巨大经济损失[1]，因此提高输电线的抗冰承载能力的研究具有重要意义。工程中一般采用融冰技术提高输电线的抗冰能力[2]，但技术相对复杂且难度较大。本文基于悬索模型，通过对悬线高差与冰厚关系的研究，提出增加两输电塔之间悬线的高差可以相应地提高输电线承受冰载的能力，从而为增强输电线的抗冰能力提供了一个新思路。

1 输电线力学模型

设输电线沿索长均匀分布的载荷集度为q，档距为l，支座高差为h，悬索总长度为S，弧垂为fa，fb，悬线最低点距离A端塔架为a，距离B端塔架为b，悬索最低点的拉力为Ft0，如图1-图2所示。

1.1 悬索的求解方程

通过对悬索力学分析[3]得到悬链线方程:

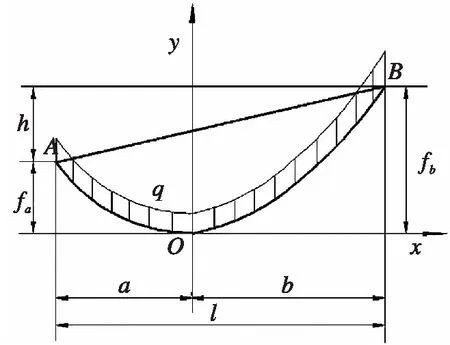
图1 输电线模型Fig.1 The model of transmission line

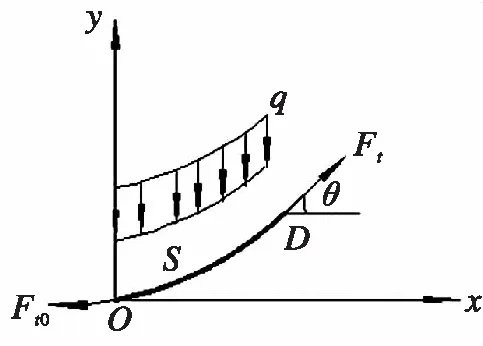
图2 输电线受力图Fig.2 The force of transmission line

(1)

悬索总长的计算公式为:

(2)

将A、B两点坐标(-a，fa)、(b，fb)代入式(1)中，可求得a、b为:

(3)

(4)

于是:

(5)

方程(5)为超越方程，未知量为Ft0，本文通过MATLAB软件采用Newton与Steffensen迭代法编程求解。

1.2 悬索最低点的拉力

由式(2)-式(4)，并考虑到l=a+b，fb-fa=h，即可得到悬索最低点的拉力。简化运算如下：

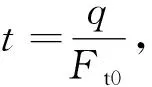
sinh(at)+sinh(bt)=tS

(6)

将式(3)、式(4)取反函数后得到：

上述两式相减并用t替换后得到:

cosh(bt)-cosh(at)=th

(7)

由式(6)、式(7)结合双曲函数的性质得到:

ebt-e-at=t(S+h)

(8)

eat-e-bt=t(S-h)

(9)

将式a、b几何关系分别带入式(8)、式(9)后得到:

ebt(1-e-lt)=t(S+h)
e-bt(elt-1)=t(S-h)

两式相乘后得到方程(10)，方程中仅含有一个未知量t，故进而可以求得Ft0.

(10)

1.3 悬索上任意一点的拉力

(11)

将式(1)代入得：

Ft=Ft0+qy

(12)

支座A、B处的拉力为:

FtA=Ft0+qfa

(13)

FtB=Ft0+qfb

(14)

由方程(5)可知，Ft0与fa呈非线性关系，无法直观得到FtA，FtB与高差h的变化关系，故本文通过MATLAB软件进行求解并对计算结果进行处理，得出增加两塔之间的高差可有效提高导线的覆冰承载能力的结论。

2 实例计算

2.1 参数选择与载荷计算

对于110 kV高压架空线路，由文献[1]获得其导线参数。导线型号为钢芯铝绞线：LGJ-240/40，参考GB1179-83，每公里导线质量v=964.3 kg/km，架空线路计算直径d=21.66 mm，拉断力[F]=83 370 N，杆高允许弧垂[f]=6 m，并由最大弧垂曲线得到水平档距l=300 m，塔高H=20 m，设计覆冰厚度b选为15 mm，悬垂绝缘子串由7片绝缘子组成，重量Fu=0.42 kN.

导线自重荷载为:

g1=9.8v=9.8×964.3×10-3=9.45 N/m

冰重荷载计算公式为[4-5]:

g2=0.9πb(b+d)g×10-3=27.73b(d+b)×10-3N/m

自重加冰重荷载为：g3=g1+g2.

2.2 悬链线图形的绘制

首先考虑两塔等高的情况，通过程序编制求解方程(5)解得悬链线最低点拉力Ft0.

Newton迭代法：Ft0=18 760 N，初始迭代值cz=20，迭代次数6；

Steffensen迭代法：Ft0=18 760 N，初始迭代值cz=20，迭代次数7；

进而求得a=b=150 m，悬链长度S=300.32 m．

同时考虑高差为40 m、80 m时，相应计算参数如表1所示，此时悬链线的形状如图3所示。

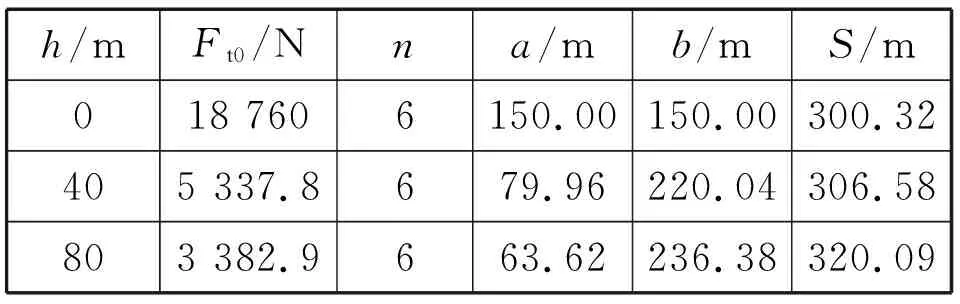
表1 计算参数Tab.1 The parameters of calculation

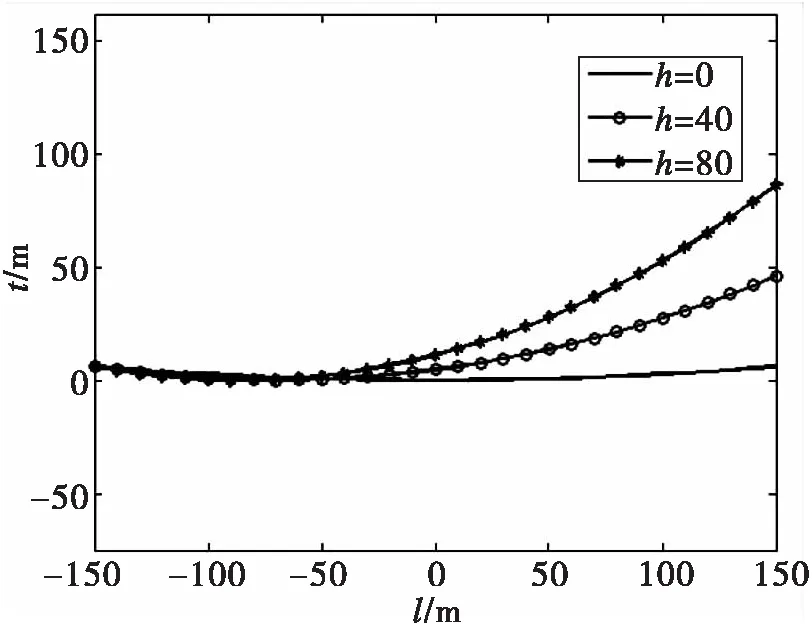
2.3 覆冰厚度与悬挂点导线张力关系

当导线悬挂点等高时，近似认为覆冰均匀分布在导线上，此时导线所受荷载为g3，选取设计冰厚b=15 mm，此时g2=27.73×15×(15+21.66)×10-3=15 N/m，g3=25 N/m，则悬线的各项受力参数如表2所示。

表2 悬链线各项受力参数Tab.2 The parameters of various mechanical forces

其中FCAx与FCAy分别为输电塔所受悬线的水平与竖直力。本文考虑重冰区导线的抗冰能力，故覆冰厚度选取0～60 mm[6].

在两塔高差一定时，随着冰厚的逐渐增加，绘制冰厚与悬挂点导线张力的关系，A、B两点的拉力大小相等，故仅绘制b-FtA，如图4所示。

图4 冰厚与悬挂点导线张力的关系Fig.4 The relationship of ice thickness and suspensionpoint wire tension

从图中可以观察到，当覆冰厚度为25 mm时，悬挂点最大张力达到导线的拉断力；但是在冰厚超过25 mm的重冰区，导线会被拉断而发生覆冰事故，导线的设计不符合要求。

2.4 高差与悬挂点导线张力关系

在跨度l一定，两端高差h变化的情况下，对悬挂点受力的大小进行分析。分别选取不同冰厚进行绘制高差与导线张力的关系图h-FtA，h-FtB，如图5、图6所示。

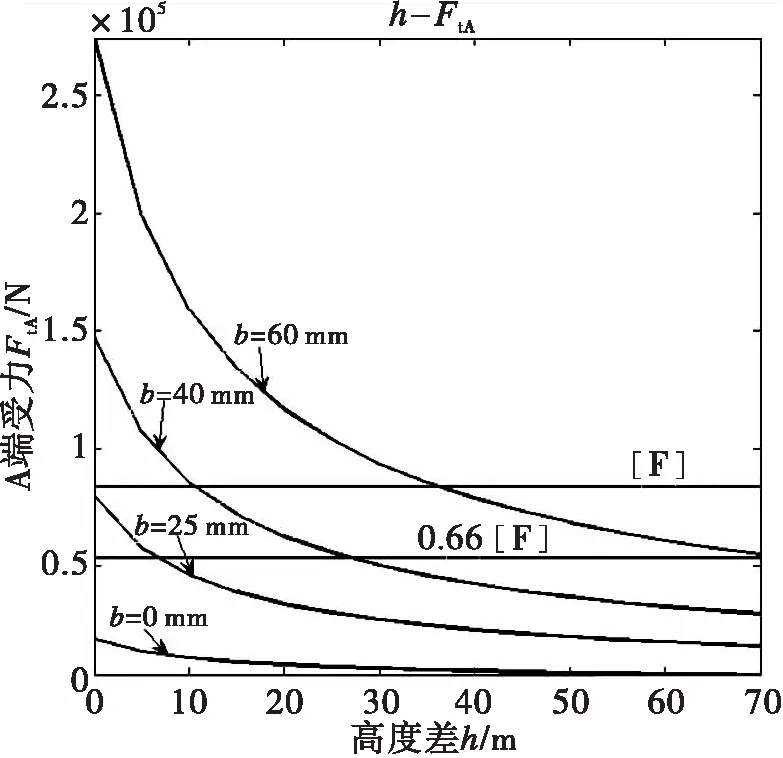
图5 高差与A端受力关系Fig.5 The relationship of height difference andforce on A side

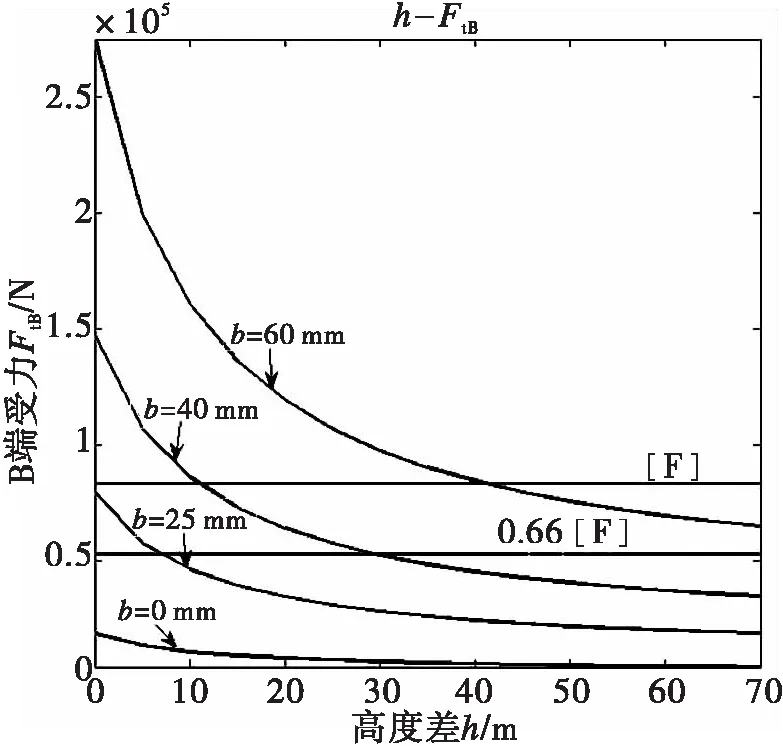
图6 高差与B端受力关系Fig.6 The relationship of height difference andforce on B side

图5、图6中第一条横线为导线拉断力基准线，第二条横线为导线设计许可张力基准线(悬挂点许可张力不超过拉断力的66%[7])。

由图5、图6知，随高差增加，导线的张力呈减小趋势；高差在0～10 m之间时，随着高差增加，导线张力显著下降；高差超过30 m时，增加高差，导线张力降低不明显；高差为6 m时，能够保证覆冰厚度为25 mm时，不超过设计许可张力。为保证导线的悬挂点的张力不超过设计许可张力，不同覆冰厚度情况下所需悬线高差如表3所示。考虑到实际情况，表3只列出高差小于15 m时覆冰厚度与所需高差对应关系。

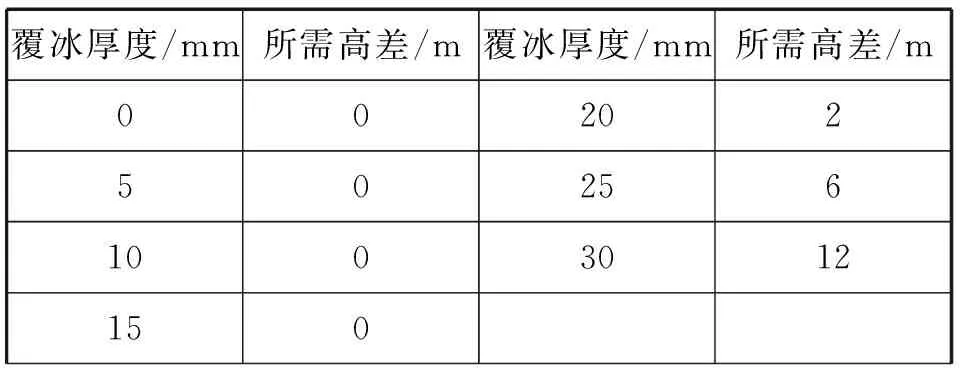
表3 覆冰厚度与所需高差Tab.3 The ice thickness and height difference

3 结论

通过对110 kV高压架空输电线覆冰厚度与导线张力关系的分析，得出如下结论：

(1)若等高架线，则覆冰厚度为25 mm时，悬挂点导线的张力达到拉断力(83 370 N)；但在冰厚超过25 mm的重冰区，若等高架线，导线会被拉断而发生覆冰事故。

(2)若设计两塔之间悬线高差为6 m，则覆冰厚度为25 mm时，悬挂点导线的张力不超过许可张力(83 370 N×66%=55 024 N)，符合设计要求。

(3)悬线的高差在0～10 m之间时，可大大降低覆冰对导线的张力，因此适当增加两塔之间悬线的高差可有效提高导线的覆冰承载能力。

参考文献：

[1] 李庆峰，范峥，吴穹．全国输电线路覆冰情况调研及事故分析[J].电网技术，2008，32(9)：33-36.

[2] 李宏力.提高输电线路融冰工作效率的技术措施[J].广西电力，2012，35(1)：42-46.

[3] 肖明葵.理论力学[M].北京：机械工业出版社，2007.

[4] 曹圩娣，梁清香，白可.覆冰对某传输塔影响的研究[J].太原科技大学学报，2011，32(2)：138-141.

[5] 阳林，郝艳捧，黎卫国.架空输电线路在线监测覆冰力学计算模型[J].中国电机工程学报，2010，30(19)：101-105.

[6] 刘树堂.输电塔结构及其设计[M].北京：中国水利水电出版社，2005.

[7] DL/T5092-1999P，110 kV-750 kV架空送电线路设计技术规程[S].北京：中华人民共和国发展和改革委员会，1999.