弯曲型输电线电磁耦合的时域建模分析方法

叶志红，石艳超，吴小林

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引言

输电线作为国家电网的重要组成部分，其工作状态的安全与稳定至关重要。处于强电磁脉冲辐照下的输电线，将遭受严重的电磁干扰，因为强电磁脉冲通过输电线耦合产生过电压信号，进而对输电线端接装置造成毁伤，影响供电系统安全[1-2]。因此，研究强电磁脉冲作用架空输电线的电磁耦合问题，获得可靠的过电压响应数据，为输电线电磁防护设计提供理论支撑。

目前，国内外学者关于输电线的电磁耦合已开展相应数值计算方法研究。首先，全波算法是输电线电磁耦合最直接的数值方法，例如时域有限差分(Finite Difference Time Domain,FDTD)方法[3-4]、时域有限元法[5]和矩量法[6]等。但是，全波算法需要对输电线精细结构直接建模，势必造成计算资源的浪费。

之后，国内外学者基于传输线理论，提出了几种高效的场线耦合算法，避免了输电线结构的直接建模，其中主流方法包括BLT方程[7-9]、FDTD-TL算法[10-13]等。BLT方程通过节点和管道的方式构建空间电磁场与输电线节点电压和电流之间的关系矩阵，并对矩阵进行求解得到节点响应。但是，传统的BLT方程是一种频域方法，单次计算只能获得一个频点的响应，对于宽频段的强电磁脉冲，计算效率低。FDTD-TL算法的思想是使用传输线方程描述空间电磁场作用传输线的耦合过程，并使用FDTD方法对空间电磁场分布和传输线方程进行求解，获得传输线及其端接负载上的电压和电流响应。相较于BLT方程，该算法的优势在于从时域角度实现了空间电磁场辐射与传输线瞬态响应的协同计算。但是，目前该算法主要是针对直导线开展的电磁耦合建模研究。然而，实际架空输电线受重力作用，呈现弧垂弯曲形态，而且受杆塔架设方位的影响，输电线的走线方向不断变化，即为斜置状，FDTD-TL算法无法直接应用。

因此，本文基于FDTD-TL算法，结合Agrawal场线耦合模型和坐标变换，提出了一种高效的时域混合算法，实现任意方位的弯曲型输电线电磁耦合快速计算。

1 时域混合算法理论

图1给出了空间电磁场作用弯曲输电线的电磁耦合模型，输电线按照任意方向架设在地面上，起点和终点位于同一水平面上，输电线高度方向为直角坐标系的z轴方向。由于重力作用，输电线呈弧垂状结构，即为弯曲形态。为了便于分析计算，输电线两端通过负载进行等效。

图1 空间电磁场作用弯曲输电线的电磁耦合模型Fig.1 Electromagnetic coupling model of curved transmission line radiated by space electromagnetic fields

由于输电线架设较高，忽略地阻抗对输电线电磁耦合的影响。此时，空间电磁场对输电线的电磁耦合作用可以通过Agrawal模型[14]的传输线方程描述为：

(1)

(2)

式中，l表示输电线在空间的走线方向；Vsca(l,t)和I(l,t)分别表示输电线沿线各点的散射电压和全电流；R(l)，L(l)，G(l)和C(l)分别为输电线不同位置处的单位长度电阻、电感、电导和电容分布参数，由于弯曲输电线沿线高度不断变化，使得输电线分布参数与空间位置有关，另外，输电线单位长度电阻和电导一般比较小，这里均设置为0，VF(l,t)为输电线的等效分布电压源项，可以表示为：

VF(l,t)=El(x,y,h,t)，

(3)

式中，El(x,y,h,t)表示输电线沿线切向电场分量。

1.1 弯曲输电线沿线坐标计算

根据式(1)和式(2)可知，弯曲输电线电磁耦合的计算精度取决于传输线方程的建模准确度。对于传输线方程，准确获得输电线单位长度分布参数和等效分布电压源项是保证建模精度的关键。由于输电线分布参数和等效分布源项均与空间位置有关，因此，获取输电线沿线各点的坐标是基础。

当弯曲输电线的中心位于直角坐标系坐标原点时(如图2所示)，输电线沿线各点的弧垂高度可以通过平抛物线方程[15]表示为：

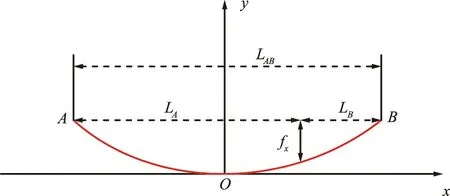
图2 弯曲输电线的弧垂计算格式Fig.2 Calculation scheme for the sag of curved transmission line

(4)

式中，fx为输电线上任意一点的弧垂高度；LA和LB分别表示输电线上任意一点到始端和终端的水平距离；g为导线自重比载N/m·mm2；τ0为导线水平应力。

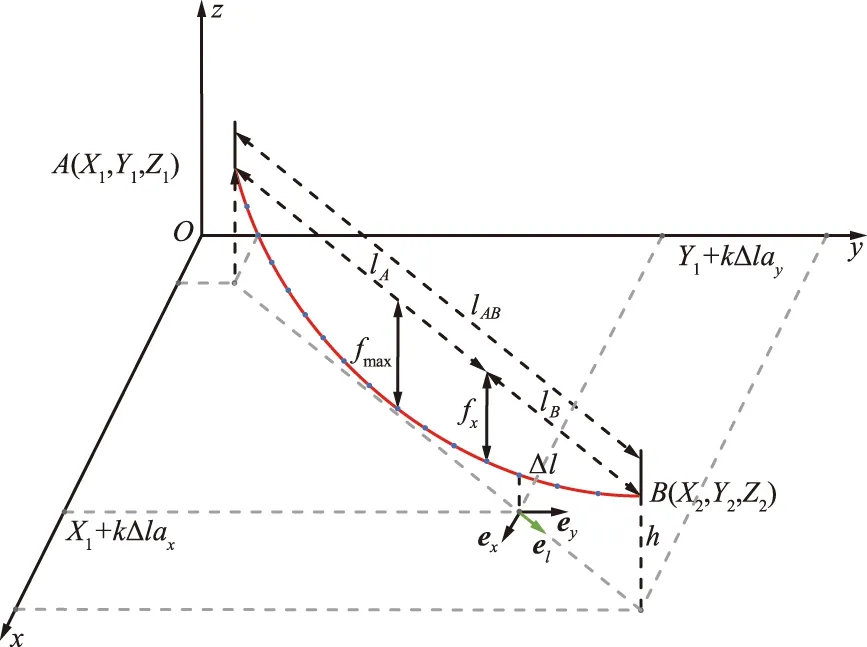
图3 弯曲输电线沿线各点坐标求解格式Fig.3 Solution scheme for the coordinates of each point along curved transmission line

1.2 弯曲输电线的单位长度分布参数计算

由于输电线沿线各点高度不同，按照FDTD网格划分之后的各段输电线单元的单位长度电容和电感分布参数亦不同。选取其中任一输电线单元，假定单元起点和终点坐标分别为(x1,y1,h1)和(x2,y2,h2)，则输电线单元中心点的高度为h0=(h1+h2)/2。由此，根据经验公式[16]，输电线单元的单位长度电容和电感分布参数由起点、终点和中心点的电容和电感分布参数求和取平均得到：

(5)

(6)

式中,ε0为自由空间介电常数；μ0为自由空间磁导率；r0为输电线半径。

1.3 弯曲输电线的等效分布源项求解

由式(3)可知，弯曲输电线的等效分布源项只由空间入射电场获得，而与输电线的散射场无关。因此，计算输电线沿线电场时，可以将输电线移除。假定入射波以任意角度入射地面，入射波的方位角、仰角和极化角分别为θ，ψ和α，有耗地面上任意位置的电场由入射波与反射波相叠加求解得到。首先，将任意极化的入射波分解为水平极化分量和垂直极化分量两部分。然后，将水平极化电场分量和垂直极化电场分量分别乘以对应的反射系数，得到反射波的水平极化电场和垂直极化电场。最后，将入射波与反射波相叠加得到，获得空间任意位置处的电场，空间任意位置处3个电场分量的频域表达式[17]为：

E0(ω)[cosαsinψcosθ(ejkzsin ψ-Rve-jkzsin ψ)+

sinαsinθ(ejkzsin ψ+Rhe-jkzsin ψ)]·

e-jkxcos ψcos θejkycos ψsin θ，

(7)

E0(ω)[cosαsinψsinθ(Rve-jkzsin ψ-ejkzsin ψ)+

sinαcosθ(Rhe-jkzsin ψ-ejkzsin ψ)]·

e-jkxcos ψcos θejkycos ψsin θ，

(8)

E0(ω)cosαcosψ[ejkzsin ψ+Rve-jkzsin ψ]·

e-jkxcos ψcos θejkycos ψsin θ，

(9)

式中，k为相位传播常数；E0(ω)为波源的频域表达式；Rv和Rh分别为垂直极化和水平极化的菲涅尔反射系数[18]。

由于输电线的弯曲形态，任一输电线单元沿线的切向电场分量无法由空间电场直接获得，需由E·el计算得到，其中E和el分别表示输电线单元中心位置处的电场和输电线单元的方向矢量(如图4所示)。

图4 输电线沿线电场求解模型Fig.4 Solution scheme for the electric fields along transmission line

电场E的3个电场分量Ex，Ey和Ez可分别由式(7)～式(9)计算并做逆傅里叶变换得到，而el由输电线单元起点和终点坐标计算得到，假定单元起点和终点坐标分别为(x1,y1,h1)和(x2,y2,h2)，则el表示为el=axex+ayey+azez，其中ax=(x2-x1)/rd,ay=(y2-y1)/rd,az=(z2-z1)/rd，rd为输电线单元起点和终点坐标的直线距离。

传输线方程构建完成之后，采用时域有限差分法的中心差分格式进行离散，得到输电线上沿线各点全电流和散射电压的迭代公式为：

(10)

(11)

2 数值仿真验证

选取户外低压10 kV的输电线为算例原型，使用时域混合算法对电磁波作用地面上单根和多根斜置弯曲输电线的电磁耦合进行数值模拟，并与矩量法的仿真结果进行对比，验证所提算法的正确性和高效性。

无限大地面上单根斜置弯曲输电线的电磁耦合模型如图5所示，地面设定为PEC。输电线始端和终端位置坐标分别为(-200,-150,10 m)和(200,150,100 m)，两端距地高度为h=10 m，输电线水平档距为L=500 m，导线最大弧垂为3.14 m。输电线选用LGJ150/25钢芯铝绞线，导线半径为8.55 mm，导线两端均接匹配负载为465.15 Ω。入射波为雷电电磁脉冲[19]，垂直照射输电线，波形表达式为：E(t)=E0[exp(-αt)-exp(-βt)]，其中E0=51 946 V/m，α=1.1×105s-1，β=3×106s-1。

图5 单根弯曲型输电线的电磁耦合模型Fig.5 Electromagnetic coupling model of single curved transmission line

图6给出了时域混合算法与MOM模拟得到的端接负载电压响应对比曲线。为了验证2种方法计算结果的正确性，使用特征选择评估(Feature Selective Validation,FSV)方法[20-21]的幅值差异量(Amplitude Difference Measure,ADM)对2种方法的仿真结果数据进行误差分析，如图7所示。FSV方法将评估结果分成极好(Excellent,EX)、很好(Very Good,VG)、好(Good,G)、一般(Fair,F)、差(Poor,P)和较差(Very Poor,VP)6个等级。从图7可以看出，2种方法的计算结果好以上等级的吻合度达到100%，验证了时域混合算法的正确性。为进一步说明时域混合算法的高效性，表1给出了所提算法与MOM计算所需网格数和占用时间对比情况。由表1可以看出，时域混合算法相较于MOM节省了大量的剖分网格数和计算时间，这是因为时域混合算法无需对地面和输电线进行直接建模。

(a) RS上电压响应

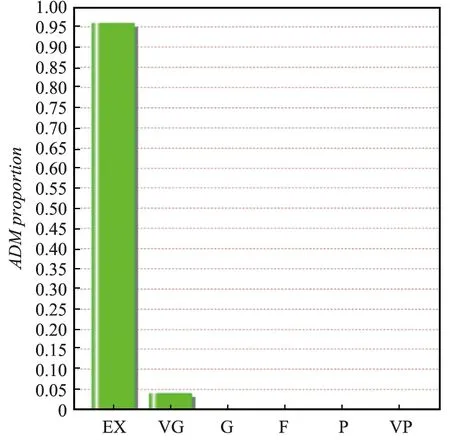
(a) RS上电压的ADM直方图

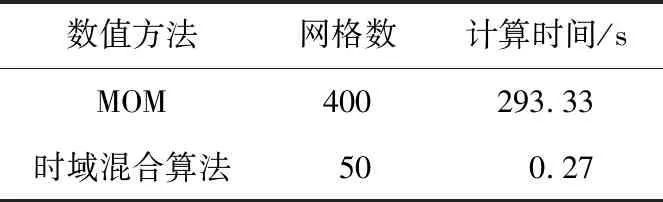
表1 算例1中2种方法计算所需网格数和计算时间Tab.1 Mesh number and computation time needed for both methods in the first case

地面上多根斜置弯曲输电线的电磁耦合模型如图8所示，地面同样为PEC。2根输电线始端和终端位置坐标分别为(-200，-150，10 m),(200，150，10 m)和(-202.4，-146.8，10 m),(197.6，153.2，10 m)，两端距地高度均为h=10 m，水平档距为L=500 m，最大弧垂为3.14 m。输电线选用LGJ150/25钢芯铝绞线，导线半径为8.55 mm，间距为d=4 m，输电线端接负载为RS1=RL2=RS2=RL2=454.78 Ω。入射波为雷电电磁脉冲，垂直照射输电线，波形和角度均与算例1相同。

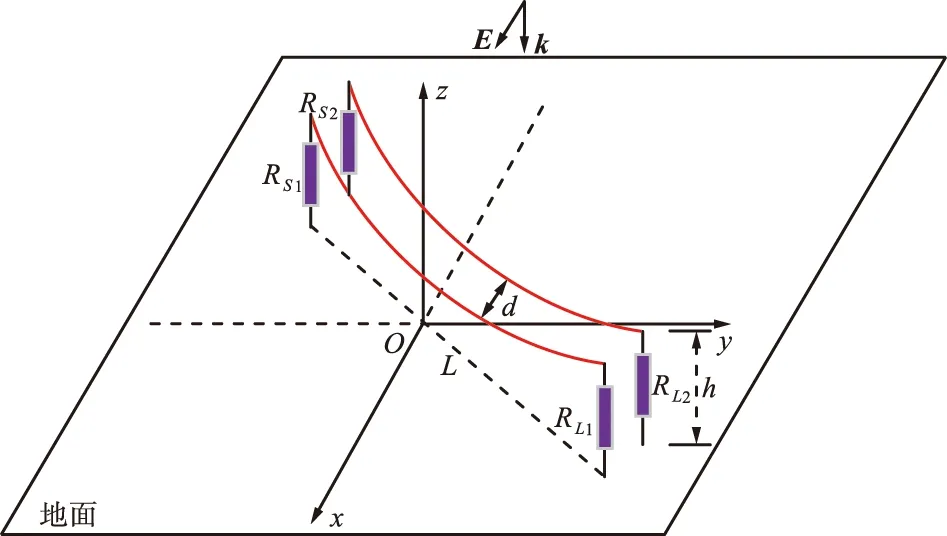
图8 多根斜置弯曲输电线的电磁耦合模型Fig.8 Electromagnetic coupling model of multiple oblique curved transmission lines

图9为时域混合算法与MOM模拟得到的端接负载RL1和RS2的电压响应对比曲线。同样，利用FSV方法的ADM指标对2种方法的仿真结果数据进行误差分析，如图10所示。可以看到，2种方法的计算结果仍能保证85%以上的较好吻合度。同样地，表2给出了时域混合算法与MOM计算所需网格量和计算时间的对比结果，验证了时域混合算法模拟多根斜置弯曲输电线电磁耦合的高效性。

(a) RL1上电压响应

(a) RL1上电压的ADM直方图

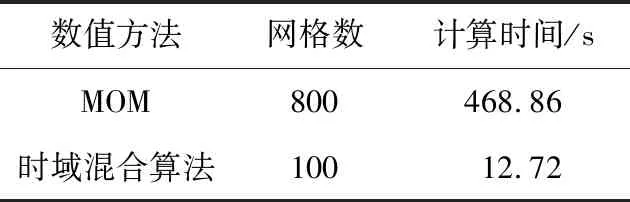
表2 算例2中2种方法计算所需网格数和计算时间Tab.2 Mesh number and computation time needed for both methods inthe second case

3 结束语

针对弯曲型输电线的强电磁脉冲耦合问题，开展了高效的时域混合算法研究。首先，根据输电线弧垂弯曲的结构特点，基于坐标变换，推导了空间任意分布的弯曲型输电线沿线各点的位置坐标。然后，采用Agrawal模型的传输线方程，构建了空间电磁场作用弯曲输电线的电磁耦合模型，并使用FDTD中心差分格式对其进行离散，迭代求解得到输电线沿线各点的瞬态电压和电流响应。通过相应算例的数值模拟，并将时域混合算法的模拟结果与全波算法矩量法的仿真结果进行了对比。仿真结果表明，所提算法具有与全波仿真相同的计算精度，同时避免了对输电线结构的直接建模，节省了大量计算时间。本文研究成果将为后续开展实际多方位输电线网络的电磁耦合建模研究奠定基础。