固定结合面切向接触阻尼分形模型
姜 来,张学良,陈永会,兰国生,温淑花,张 颖,杨 波
(太原科技大学机械工程学院,太原 030024)
结合面接触问题的接触实质是分布于两个粗糙表面上的微凸体之间的相互作用,实际工程表面的粗糙性决定结合面间的接触并非理想的完整接触。为了探究结合面接触机理,能够更精确地表征结合面的接触行为,国内外学者对结合面的接触机理做了大量的研究,并提出了不同的接触模型来描述结合面接触机理[1-6]。Yan等[7]首先提出了可以更精确描述粗糙表面形貌的三维分形模型,但并没有讨论弹塑性变形阶段的接触情况。金守峰等[8]则考虑了微凸体弹性、弹塑性和完全塑性变形三个阶段下的接触载荷和接触面积,对三维粗糙表面接触模型进行了修正。文献[9]利用有限元法分析探讨了粗糙峰弹塑性接触变形区域的行为,由曲线回归所得到的关系式,在弹塑性区域的边界上不连续。本文基于三维接触分形理论,并结合弹塑性边界连续的接触理论模型,建立了固定结合面切向接触阻尼分形模型,进而进行了数值仿真。
1 考虑弹塑性的接触载荷模型
结合面问题从本质上讲是粗糙表面间的接触问题,为了简化问题,通常将两粗糙表面的接触简化为一个等效粗糙表面与一理想刚性平面的接触。
建立在三维接触分形理论基础上的单个微凸体的等效变形量和等效半径为[7]:
(1)
(2)
微凸体由弹性接触向弹塑性接触转变时的临界变形量和临界接触面积为[7]:
(3)
K=0.454+0.41v
(4)
(5)
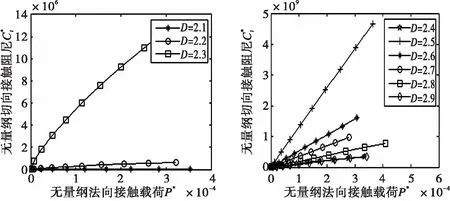
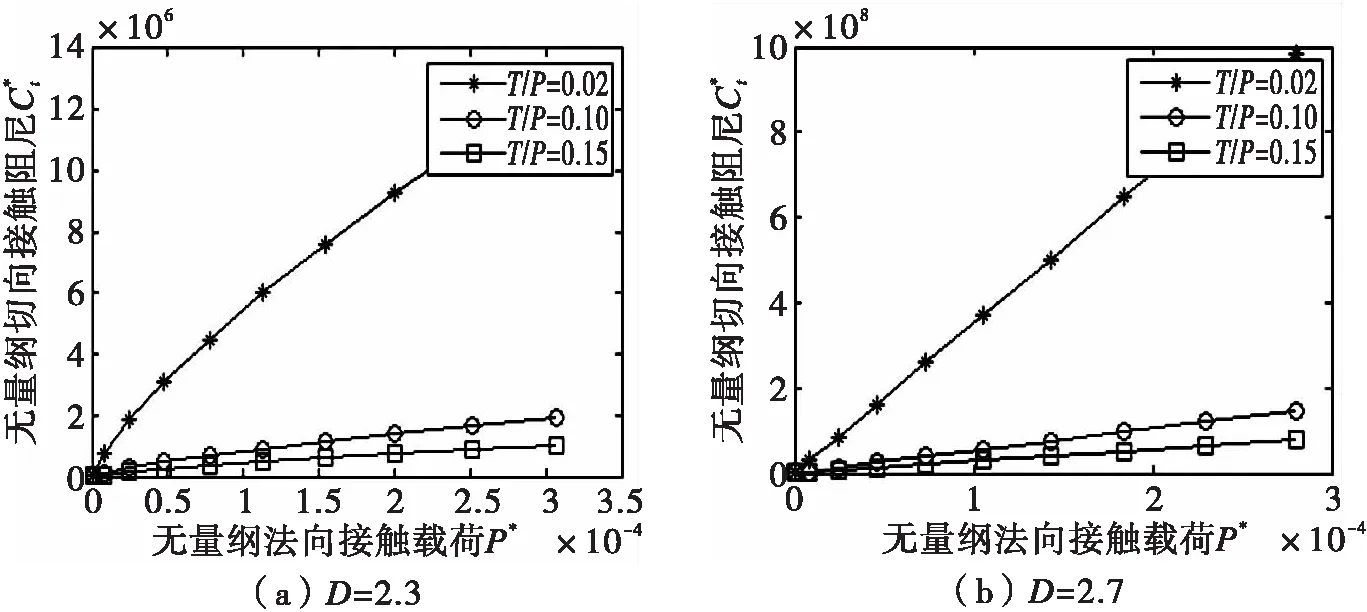
式中:D—表面分形维数,2 γ—尺度参数,基于表面光滑度和频谱分布密度考虑,γ=1.5; G—分形特征长度尺度参数; H—较软材料的硬度; E—等效弹性模量; v—较软材料的泊松比; K—硬度系数。 大多文献只研究了完全弹性变形和完全塑性变形,而没有考虑弹塑性变形的情况。实际上,弹性阶段与塑性阶段是整个变形过程中的两个连续阶段,且结构内部可能同时存在弹性区和塑性区。K-E模型[9]利用有限元法探讨了表面粗糙峰弹塑性区域的行为,由曲线回归所得到的关系式,在弹塑性区域的边界上不连续。而L-L模型[10]则改变了边界上不连续的问题,并得出了在δc≤δ≤76.4δc范围内时球形微凸体处于弹塑性状态。 L-L模型[10]所提出的弹塑性区域接触载荷、接触面积关系式为: (6) 当微凸体发生弹性变形时,根据Hertz接触理论,微凸体的接触面积和接触载荷分别为: (7) 当微凸体发生完全塑性变形时,微凸体的接触面和接触载荷分别为: (8) 粗糙表面上的横截微凸体大小分布函数为[7]: (9) 式中a′为接触点截断接触面积且与实际接触面积关系为a′=2a. 因此,考虑弹塑性过度变形机制的接触总载荷为: (10) 将式(1)、式(2)、式(6)-式(9)代入式(10)并行无量纲化得: (11) 由文献[11]知,在法向载荷p和切向载荷t作用下球形微凸体与平面接触时,其切向等效弹性变形量为: (12) 切向载荷在一个周期内所做的功为: (13) 基于文献[4]的三个基本假设可得作用于单个微凸体上的切向载荷t、法向载荷p分别为t=aT/Ar和p=aP/Ar,且T是作用在整个固定结合面的切向动态载荷幅值;P是作用在整个固定结合面的法向预加载荷即法向接触载荷;Ar则为固定结合面的真实接触面积。整个固定结合面上切向载荷T在一个周期内所做的功为: (14) 在切向载荷t作用下,单个球形微凸体和平面接触在一个振动周期内的切向接触阻尼耗能为[11]: (15) 根据固定结合面切向接触阻尼耗能机理,固定结合面的切向接触阻尼耗能为[12]: (16) 根据阻尼损耗因子定义,固定结合面切向接触阻尼损耗因子为: η=Wd/(We-Wd) (17) 而固定结合面切向接触阻尼属于迟滞阻尼[11],因此,切向接触阻尼为: Ct=ηKt (18) 根据文献[14],弹塑性区域边界连续的微凸体的切向接触刚度为: (19) 将式(9)、式(14)、式(16)、式(17)、式(19)代入式(18)可得整个固定结合面的切向接触阻尼为: (20) 对式(20)无量纲化,得: (21) 其中, 图2 G*对的影响(k=2.8,φ=2.5,T/P=0.02,μ=0.30)Fig.2 The influence of G* on 图3 φ对的影响(k=2.8,G*=1.0×10-10,T/P=0.02,μ=0.30)Fig.3 The influence of φ on 图4 T/P对的影响(k=2.8,φ=2.5,G*=1.0×10-10,μ=0.30)Fig.4 The influence of T/P on 仿真结果表明: (1)固定结合面无量纲切向接触阻尼会随着无量纲法向接触载荷的增大而增大,如图1所示。当分形维数D=2.1~2.5时,无量纲切向接触阻尼会随着分形维数的增大而增大;分形维数D=2.6~2.9时,无量纲切向接触阻尼会随着分形维数的增大而减小。 (1)建立了基于三维接触分形理论的弹塑性区域边界连续的固定结合面切向接触阻尼分形模型。 (2)固定结合面无量纲切向接触阻尼和无量纲法向接触载荷之间关系随着分形维数的变化而呈微凸弧非线性关系(D=2.1~2.4)和近乎线性关系(D=2.6~2.9);当D=2.1~2.5时,无量纲切向接触阻尼随着分形维数D增大而增大;当D=2.5~2.9时,无量纲切向接触阻尼随着分形维数D增大而减小。 (3)固定结合面无量纲切向接触阻尼随着塑性指数φ增大而增大,随着分形粗糙度参数G*、T/P的增大而减小。 参考文献: [1] MJUMDAR A,BHUSHAN B.Fractal Model of Elastic-plastic Contact between Rough Surfaces[J].J Tribol,1991,113:1-11. [2] 温淑花,张学良,武美先,等.结合面法向接触刚度分形模型建立与仿真[J].农业机械学报,2009,40(11):197-202. [3] 温淑花,张学良,武美先,等.结合面切向接触刚度分形模型及其仿真[J].农业机械学报,2009,40(12):223-227. [4] 张学良,温淑花,兰国生,等.平面结合面切向接触阻尼分形模型及其仿真[J].西安交通大学报,2011,45(5):74-77,136. [5] 尤晋闽,陈天宁.基于分形接触理论的结合面法向接触参数预估[J].上海交通大学学报,2011,45(9):1275-1280. [6] 田红亮,朱大林,秦红玲.结合面静摩擦因数分形模型的建立与仿真[J].应用力学学报,2011,28(2):158-162. [7] YAN W,KOMVOPOULOS K.Contact analysis of elastic-plastic fractal surfaces[J].Journal of Applied Physics,1998,84:3617-3624. [8] 金守峰,宿月文,郭彩霞.三维分形粗糙表面的修正接触模型[J].中国机械工程,2012,23(19):2316-2319. [9] KOGUT L,ETSION I.Elastic-plastic contact analysis of asphere and a rigid flat[J].ASME Journal of Applied Mechanics,2002,69(5):657-662. [10] LIN L P,LIN J F.An asperity microcontact model developed for the determination of elastoplastic deformation regime and contact behavior microasperity[J].ASME J Tribol,2004,127:666-672. [11] 张学良,王南山,温淑花.机械结合面切向接触阻尼能量耗散弹塑性分形模型[J].机械工程学报,2013,49(6):43-49. [12] JOHNSON K L.Contact mechanics[M].Cambridge:Cambridge university press,1985. [13] BOGRAD S,SCHMIDT A,GAUL L.Joint damping prediction by thin layer elements[C]∥Proceedings of IMAC 26th,society of experimental mechanics Inc.Bethel,Connecticut,US,2008. [14] 牛作证,张学良,温淑花.结合面切向接触刚度三维分形模型[J].太原科技大学学报,2013,34(5):361-367. [15] 刘正伦.具可变形貌参数之微接触模型理论研究[D].台湾:国立成功大学,2006. [16] YOU J M,CHEN T N.Statistical model for normal and tangential contact parameters of rough surface[J].J Mechanical Engineering Science,2010,225:171-185. [17] JIANG SHUYUN,ZHENG YUNJIAN.A contact stiffness model of machined joint surfaces[J].ASME Journal of Tribology,2000,132(1):1-7.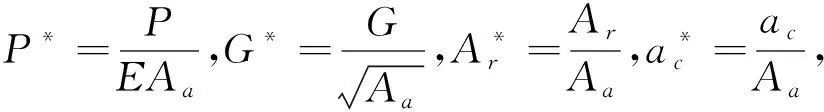
2 弹塑性区域边界连续的固定结合面切向接触阻尼分形模型


3 模型仿真与讨论



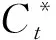
4 结论

