一类具有功能反应的非线性捕食系统的定性分析①

李晓艳， 霍锦霞， 李曼生， 田丽娜

(兰州城市学院数学学院，甘肃兰州 730070)

0 引言

捕食与被捕食系统的动力学行为是数学生态学的一个非常重要的课题，特别是关于极限环的存在性问题，在这方面已有许多研究成果.本文研究如下既具有功能反应又具有密度制约的非线性种群系统:

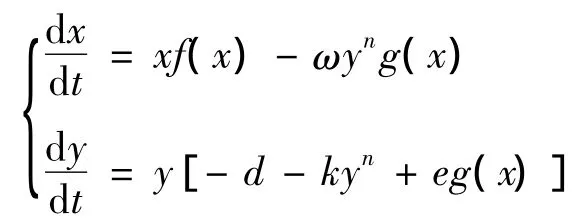
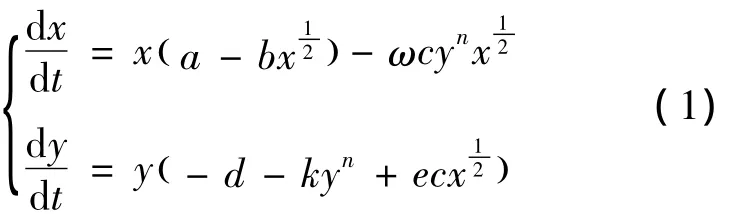
考虑到系统的实际意义，仅在集合R+中研究A≥1的情形，作变换，则模型(1)可化为

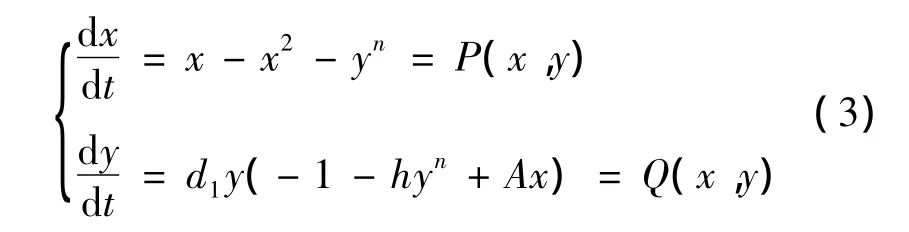
1 平衡点及其性态分析

下面判定奇点的性态，易得到:O(0，0)为系统(3)的鞍点;R1(1，0)为系统(3)的鞍点;

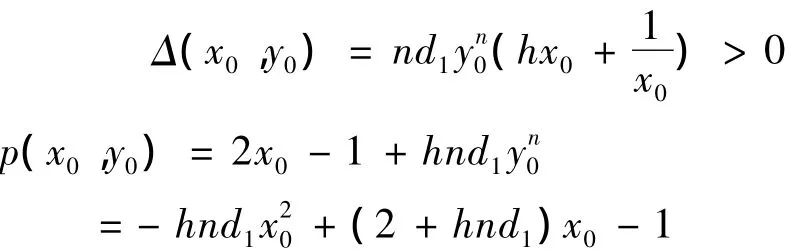
令p=0可解得:

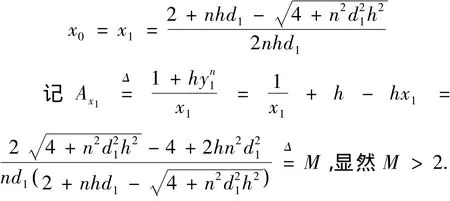
则A＞M时p(x0，y0)＜0;A＜M时p(x0，y0)＞0;A=M 时，p(x0，y0)=0.

综上所述，可得如下定理:

定理1 当A＞M时，R2(x0，y0)为不稳定的焦点或结点;当A＜M时，R2(x0，y0)为稳定的焦点或结点;当A=M时，R2(x0，y0)为中心点.

定理2 系统(3)由P(xp，yp)出发的解是有界的，其中(xp，yp)∈ R2，xp≥0，yp≥ 0.

证明: 设系统(3)由P(xp，yp)出发的解为x=x(t)，y=y(t)，作直线 x=r，r≥ max{xp，1}，则当y＞0时=r(1－r)－yn≤－yn＜0可知系统(3)的轨线经过直线x=r时，总是从右向左的;

定理3 当1＜A≤2时，系统(3)的正平衡点R2(x0，y0)在R+内是全局渐近稳定的.

证明: 当1＜A≤2时，系统(3)存在唯一的正平衡点R2(x0，y0)且为稳定的焦点或结点.下面只需证明，当1＜A≤2时，系统(3)在R+内不存在极限环.利用 Dulac函数法，取 B=xαyβ，其中 α

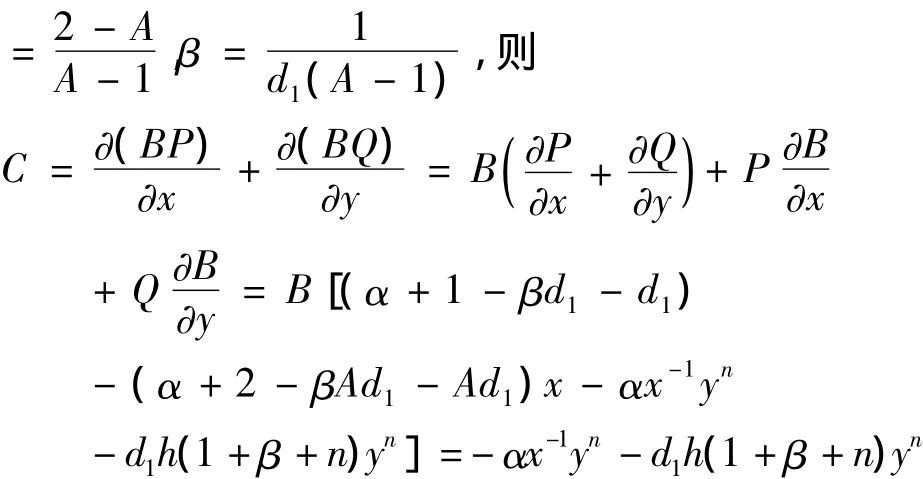
因为1 ＜ A≤2，则α≥0，β ＞ 0，C=－ αx－1yn－d1h(1+в+n)yn≤0，由Dulac函数法可得当1＜A≤2时，系统(3)在R+内不存在极限环，再根据定理3可知系统(3)的正平衡点R2(x0，y0)在内是全局渐近稳定的.

2 极限环的存在唯一性

定理4 A＞M当时，系统(3)至少存在一个包含R2点的极限环.

证明: 当A＞M时，第一象限内的正平衡点R2(x0，y0)存在且为不稳定的结点或焦点，在R2点的足够小邻域内做包含R2的闭曲线C，凡与C相遇的轨线均穿向C的外部，所以C可作为环域G的内境界线.下面构造环域G的外境界线:当y＞0时，，所以系统(3)的轨线与x=1相遇时，均从该直线的右方穿入左方.

故轨线与直线y=s相遇时均从其右上方穿入左下方.

这样由直线 x=0，y=0，x=1，y=s，围成了G的外境界线，G内部无奇点，O(0，0)和R1(1，0)均为鞍点，G内的轨线正向不能进入，由Bendixson环域定理可知G内至少存在一个包含R2点的极限环.

从生态学的角度来看，极限环的存在性意味着捕食和被捕食两种群将长期共存，而且两种群的密度大小最终趋于某一有规则的周期性振荡，两者密度同时上升(下降)，或者交替上升(下降)，周而复始，从而使两物种协同进化.

[1]Lu Zhi－ qi，Wei Ping，Pei.Li－ jun.The Stage－ structure Predator－prey Model with a Time Delay and Optimal Harvesting Policy[J].Journal of Biomathematics ，2003，18(4):390－394.

[2]Wang C，Pei Y.Global Stability for a Single－Species Plant Model with Delay in Diffusion[J].Journal of Biomathematics，2005，20:129－134.

[3]刘会民，范猛.临界退偿系统的捕获优化问题[J].生物数学学报，1998，13(4):479－483.

[4]张芷芬，丁同仁，黄文灶等.微分方程定性理论[M].北京:科学出版社，1985.

[5]Hale J.Theory of Functional Differential Equations[M].Heidelberg:Spinger Veragem，1977.