NOD序列加权和的完全收敛性①

管 梅

(合肥学院数学与物理系，安徽合肥 230601)

Ebrahimi 和 Ghosh[1]于 1981 年引入了下面NOD(negatively orthant dependent)序列的概念.

定义 1 称随机变量序列 X1，X2，…，Xk是NUOD(negatively upper orthant dependent)的，如果对于任意实数 x1，x2，…，xk有

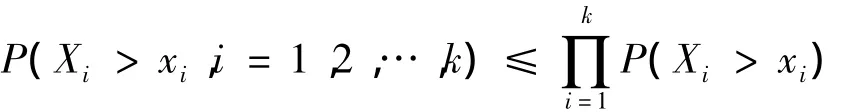
称 随 机 变 量 序 列 X1，X2，…，Xk是NLOD(negatively lower orthant dependent)的，如果对于任意实数 x1，x2，…，xk有

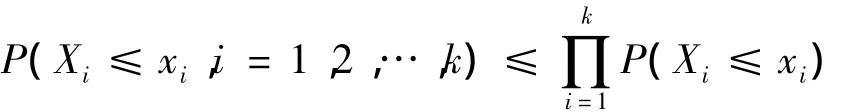
称 随 机 变 量 序 列 X1，X2，…，Xk是NOD(negatively orthant dependent)的，如果它既是NUOD的又是NLOD的.称无穷随机变量序列{Xn，n≥1}是NOD的，如果它的每一个有限子列X1，X2，…，Xn是 NOD 的.

Joag－ Dev和Proschan[2]指出任何NA随机变量序列是NOD的，但NUOD或NLOD不能推出NA，并且给出了一个是NOD但不是NA的例子，说明了NOD是严格弱于NA的.

陈瑞林[3]研究了NA列加权和的强收敛速度，获得了一些完全收敛性的结果，甘师信和陈平炎[4]将文献[3]中的结论推广到NOD序列情形.本文研究了NOD序列加权和的完全收敛性，丰富了前人的结论.

定义2 设{Xn，n≥1}是随机变量序列，称其尾概率被随机变量X一致控制，若存在非负常数C，使得对 ∀x∈ R+，有

简记为{Xn}≺X以下不妨假定X为非负的.

本文一律以C记与n无关的正常数，且C在不同的地方可表示不同的值，即使在同一式中也如此.“＜ ＜”表示通常的大“O为证本文定理，先介绍以下引理.

引理1[5](1)设 X1，X2，…，Xn是 NOD 序列，f1，f2，…，fn全部是单调增(或单调减)函数，则f1(X1)，f2(X2)，…，fn(Xn)是 NOD 的.

(2)设 X1，X2，…，Xn是非负 NOD 序列，则

引理2(见文献[6]中引理4.1.1) 设X是随机变量，且满足 X ≤1，a.s.则

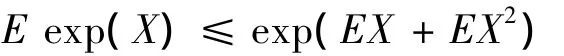
引理3(Bonferroni不等式，见文献[6]中引理4.1.2) 设{Ai，1 ≤ i≤ m}是一列事件，令

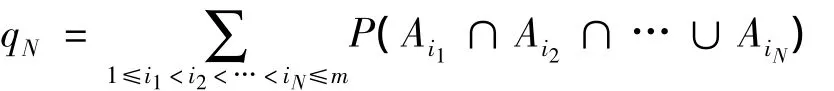
则

P(Ai中至少有N个发生)≤qN

1 主要结果及其证明

定理1 设{Xn，n≥1}是均值为零的NOD序列，{X}≺ X，EXp＜ ∞，p ＞ 0，{a，1 ≤ k≤ n，n≥1}为实数阵列，且|ank|≤Cn－α对所有n≥1，k≥1成立，其中，特别当时，有成立，则对任意ε＞0，有

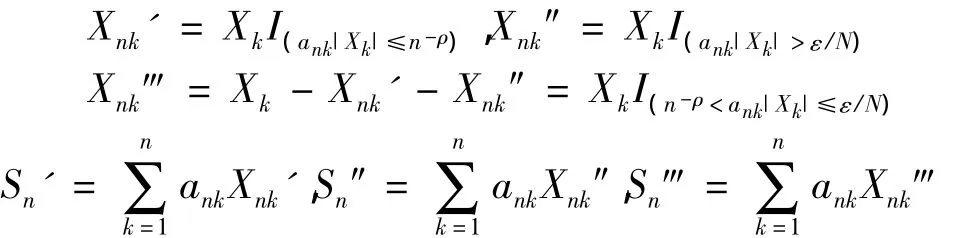
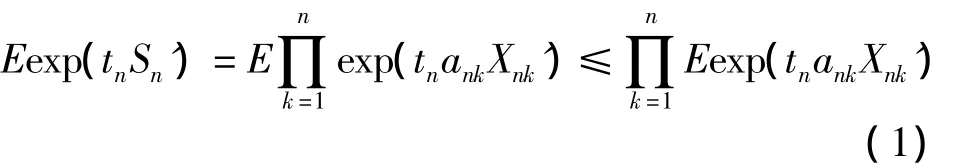
由tn的取法知，当n充分大时有tn≤nρ，也既有tnankXnk′≤1则有引理2知

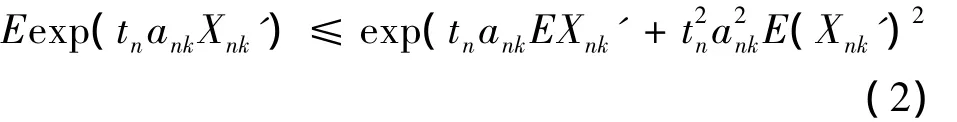
由Markov不等式，tn的取法及(1)、(2)式有

而当p＞1时，有EXk=0及仍有

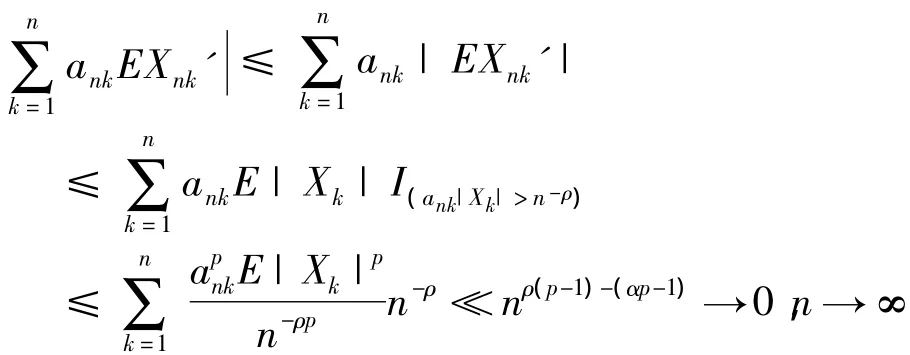
于是当p＞0时，总有(4)式成立.

当p＞2时，EX2＜∞ 注意到时显然有

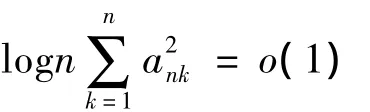
结合定理条件可得

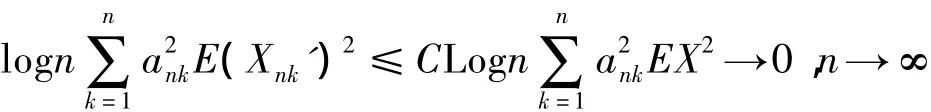
而当0＜p≤2时，由EXp＜∞ 有

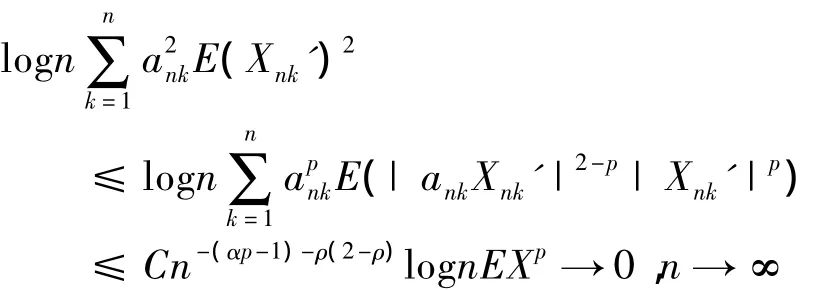
于是当p＞0时，也有(5)式成立.所以当n充分大时，由(3)，(4)，(5)式有

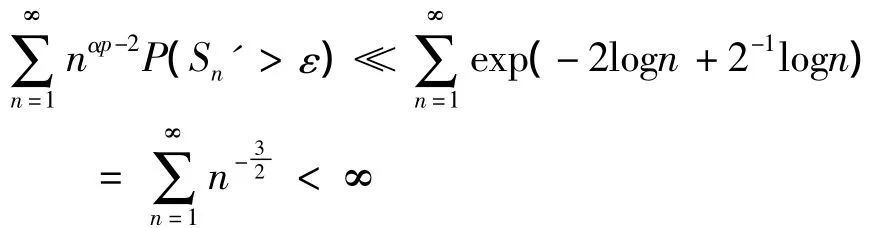
用－Xk代替Xk，同理可得

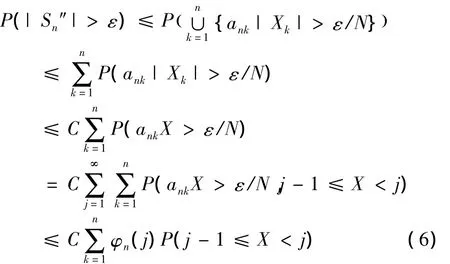
由ankX ＞ ε/N知ank＞ ε/(Nj)，结合ank≤Cn－α可知，n ＜ (jCN/ε)1/α，从而有 n ≤ φj，故由(6)式有

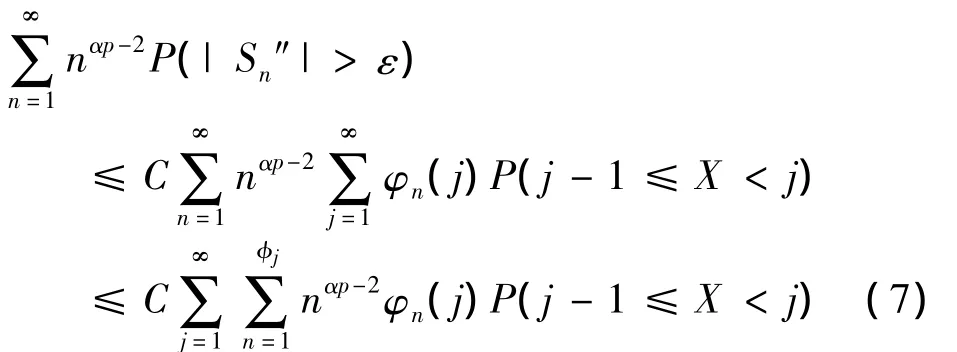
所以由(7)，(8)式可知

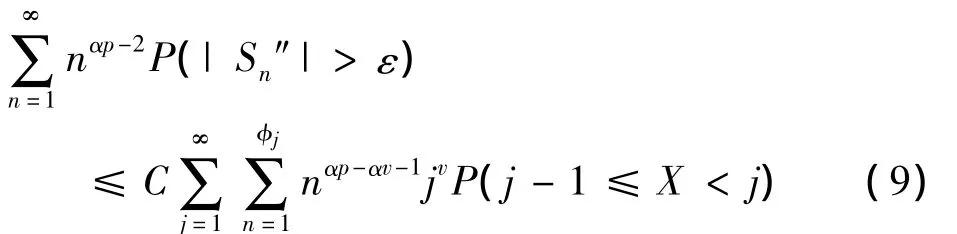
由v的取法可知αp－αv－1＞0，于是有

由(9)，(10)式及EXp＜∞ 得

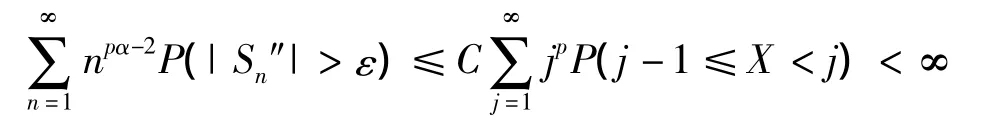
由于

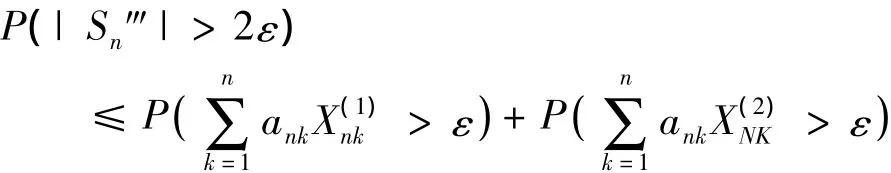
必至少存在N个k，使得n－p＜ ankXk≤ε/N，因此至少存在N个k，使得ankXk＞n－p，于是由引理3及定义1知

≤ nαp－2P(至少存在 N 个 k，使得 ankXk＞ n－p)

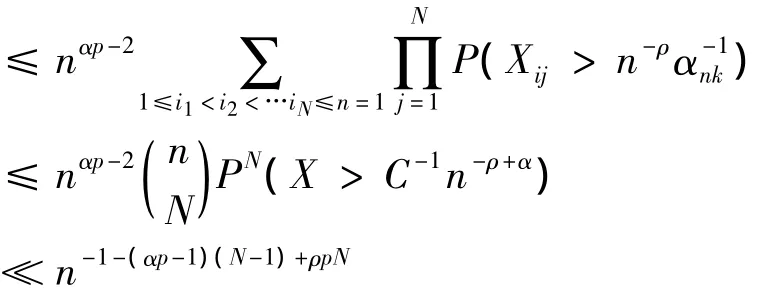
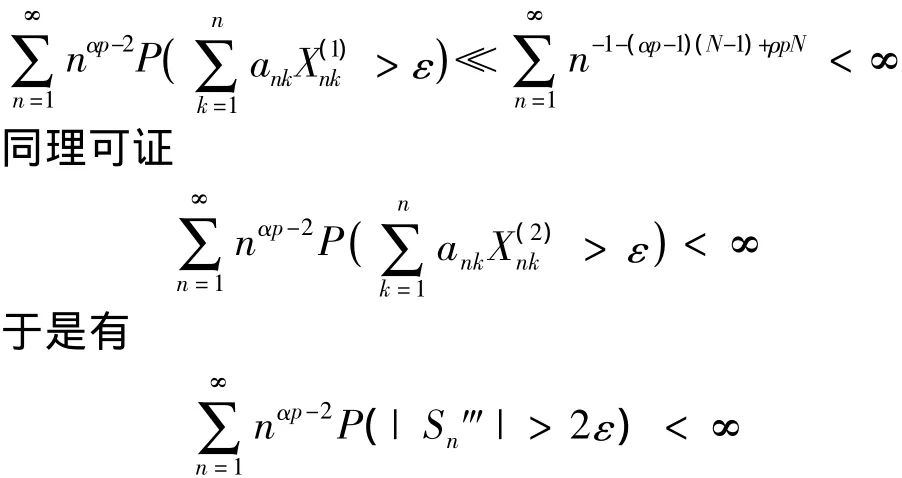
定理1证毕.

[1]Ebrahimi，N.，Ghosh，M.，Multivariate Negative Dependence，Communications in Statistics－ Theory and Methods，1981，10(4):307－337.

[2]Joag－ Dev K.，Proschan F.Negative Association of Random Variables with Applications[J].Ann Statist，1983，11:286－295.

[3]Chen R.L.Strong Convergence Rate of Sums for NA Sequences with Different Distributions[J].Chinese Journal of Applied Probability and Statistics，2004，20(1):47－53(in Chinese).

[4]Gan S.X.，Chen P.Y.Strong convergence Rate of Weighted Sums for NOD Sequences[J].Acta Mathematica Scientia，2008，28A(2):283－290(in Chinese).

[5]Bozorgnia A.，Patterson R.F.，Taylor R.L.Limit Theorems for Dependent Random Variables[J].World Congress Nonlinear Analysts＇92，1996，11:1639－1650.

[6]Stout W.F.Almost Sure Convergence[M].New York:Academic Press，1974.