带形状参数的五次Bézier曲线的扩展①

张丹丹

(安徽广播电视大学安庆分校，安徽安庆 246001)

0 引言

随着几何造型工业的发展，需要对曲线的形状进行调控或改变曲线的位置，人们开始研究推广Bézier曲线.文献[1～2]提出了含形状参数λ的二次、三次Bézier曲线的扩展，利用这一形状参数对曲线形状进行调整.为了更加灵活地对曲线的形状进行调控，文献[3]提出了带二个形状参数的二次Bézier的扩展，所生成的曲线可以灵活的进行调控.文献[4]提出了带多个形状参数的二次Bézier曲线的扩展，能够更灵活地局部或整体调控曲线的形状.文献[5]提出了两组分别含2个和3个形状控制参数的三次Bézier曲线的扩展，对于给定的控制多边形顶点，对形状参数进行调整可灵活地调整曲线的形状.文献[6～7]提出了带多个形状参数的四次Bézier曲线的扩展，得到的曲线具有四次Bézier曲线类似的性质，曲线的灵活性比较强.文献[8]给出了带一个形状参数的五次 Bézier曲线的一种新扩展.

本文针对五次Bézier曲线进行扩展，给出了两组带有形状控制参数的五次扩展Bézier曲线，能够更加灵活地调控曲线的形状.两类曲线具有五次Bézier曲线类似的性质:端点性、凸包性、对称性等等.最后，通过实例证明该曲线在曲线设计中具有一定的实际应用价值.

1 五次Bernstein基函数的扩展

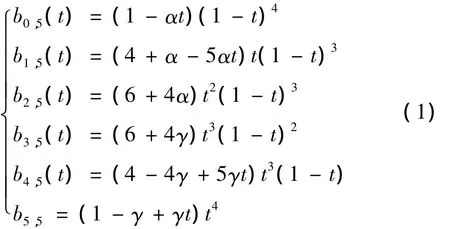
为带形状参数α，β的五次多项式基函数.当α= β =1 时，bi，5(t)(i=0，1，2，3，4，5)退化为五次Bernstein基函数.

定义2 对任意 t∈[0，1]，α，γ ∈[－ 5，1]，α + β∈[－10，5]，β + γ ∈[－10，5]称关于t的多项式

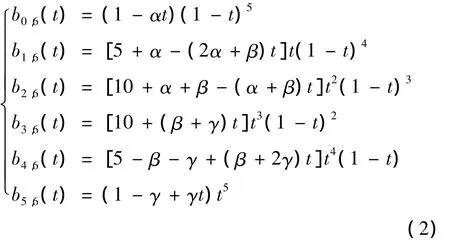
为带形状参数α，β，γ的六次多项式基函数.当α = β = γ =0 时，bi，5(t)(i=0，1，2，3，4，5)退化为五次Bernstein基函数.当α=γ=λ，β=－2λ时，bi，5(t)(i=0，1，2，3，4，5)退化为文献[8]的第四类基函数.

不难证明，上述基函数有以下性质:

性质3 对称性.当 α =γ时，b0.5(1－t)=b5，5(t)，b1，5(1－ t)=b4，5(t)，b2，5(1－ t)=b3，5(t);b0，6(1－ t)=b5，6(t)，b1，6(1－ t)=b4，6(t)，b2，6(1－ t)=b3，6(t).

性质4 端点性质.b0，k(0)=1，bi，k(0)=0(i=1，2，3，4，5)，bi，k(1)=0， (i=1，2，3，4)，b5，k(1)=1(k=5，6).

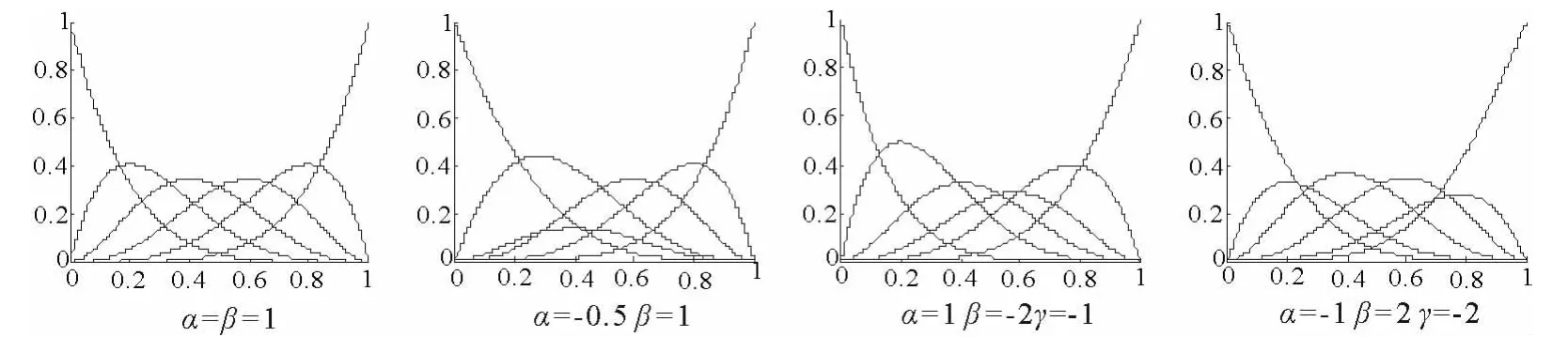
图1 两组基函数图形

2 五次Bézier曲线的定义及性质

定义3 对于给定6个控制定点Pi∈Rn(n=2，3;i=0，1，2，3，4，5)，t(0，1)定义曲线

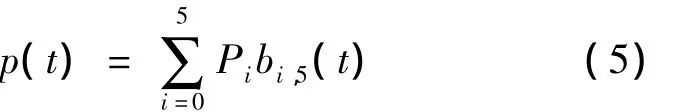
称式(3)为带形状参数α，γ的第一类五次Bézier曲线.其中bi，5(t)(i=0，1，2，3，4，5)为定义1中的多项式的基函数.当α=γ=1时退化为五次 Bézier曲线.

定义4 对于给定6个控制定点Pi∈Rn(n=2，3;i=0，1，2，3，4，5)，t(0，1)定义曲线

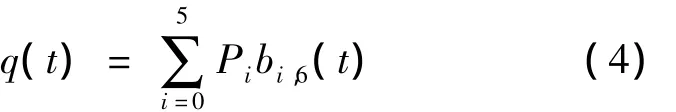
称式(4)为带形状参数α，β，γ的第二类五次Bézier曲线.其中bi，6(t)(i=0，1，2，3，4，5)为定义2中的多项式的基函数.当α=γ=0时退化为五次 Bézier曲线.

上述两类曲线具有下列性质:

(1)端点性质

(2)切矢量

(3)对称性当α=γ时，曲线p(t)，q(t)具有对称性.

(4)凸包性

(5)几何不变性和仿射不变性

图2(a)从内到外依次为α=1，γ=－1，－0.5，0，0.5，1 时的第一类五次Bézier曲线;图2(b)从内到外依次为γ =1，α =－1，－0.5，0，0.5，1时的第一类五次Bézier曲线;图2(c)从内到外依次为α=－1，β =－1，γ =－1，－2，－3，－4，－5时的第二类五次Bézier曲线;图2(d)从内到外依次为β=－1，γ =1，α =－1，－2，－3，－4，－5时的第二类五次Bézier曲线.

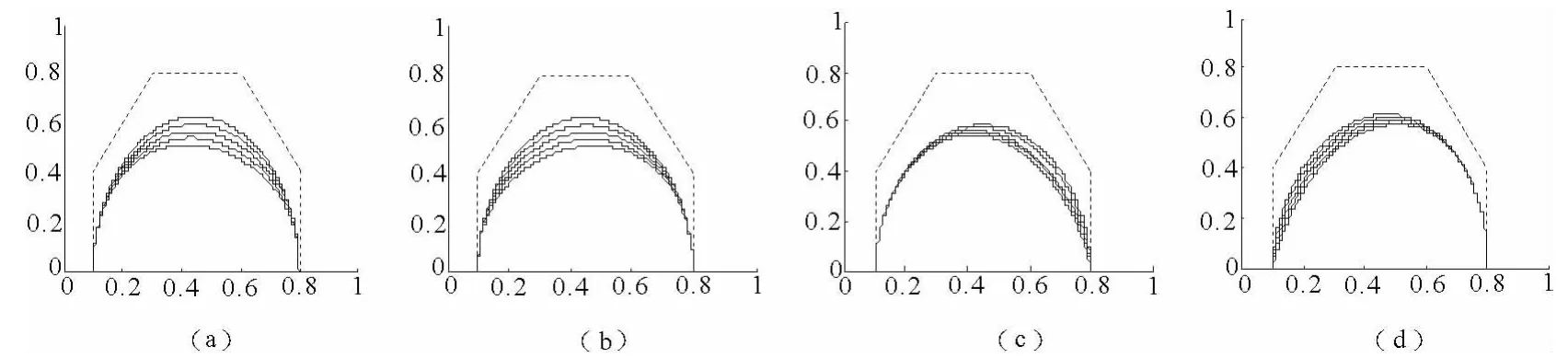
图2 不同参数值的两类曲线

3 曲线的拼接

就第二类扩展曲线q(t)来看，q1(t)，q2(t)为两条第二类扩展的Bézier曲线，其中p1(t)的控制顶点为 P0，P1，P2，P3，P4，P5;形状参数为 α1，β1，γ1;p2(t)的控制顶点为 Q0，Q1，Q2，Q3，Q4，Q5形状参数为 α2，β2，γ2.若q1(t)与q2(t)之间满足G1连续，则q1(t)的末端与q2(t)的首端位置连续即 P5=Q0，且 P4，P5(Q0)，Q1三点共线，

图3 花瓣图形

说明q1(t)，q2(t)在拼接处达到G1连续.当α2=λ(5+ γ1)－5时，有q1′(1)=q2′(0)那么q1(t)与q2(t)在拼接处C1连续.

4 应用实例

图3(a)是第一类曲线当γ =1，α =－1，0.5，0，0.5，1时生成的花瓣图形;图3(b)是第二类开曲线当 α =－1，γ =－1，β =－9，－6，－3，0，3时生成的花瓣图形;图3(c)是第一类闭曲线当α=1，γ =－ 1，－ 0.5，0，0.5，1 时生成的花瓣图形;图3(d)是第二类闭曲线当α=－1，β=－1，γ=－1，－2，－3，－4，－5时生成的花瓣图形.

[1]韩旭里，刘圣军.二次Bézier曲线的扩展[J].中南工业大学学报(自然科学版)，2003，34(2):214－217.

[2]吴晓勤，韩旭里.三次Bézier曲线的扩展[J].工程图学学报，2005，26(6):98－102.

[3]严兰兰，梁烔丰.形状可调二次Bézier曲线[J].东华理工大学学报(自然科学版)，2008，31(1):93－97.

[4]张贵仓，师利红.带多个形状参数的Bézier曲线[J].西北师范大学学报(自然科学版)，2010，46(4):24－27.

[5]秦新强，胡钢，张素霞.三次Bézier曲线的新扩展及其应用[J].计算机工程与应用，2008，44(2):112－115.

[6]朱秀梅，郭清伟，朱功勤.含多参数的四次Bézier曲线的扩展[J].合肥工业大学学报，2008，31(4):671－674.

[7]张念娟，秦新强，胡钢，党发宁.带多个形状参数的四次Bézier曲线的新扩展[J].武汉理工大学学报，2009，31(20):156－160.

[8]姜岳道，植物.Bézier曲线的扩展种类[J].内蒙古民族大学学报，2011，26(4):378－381.