截尾泊松分布参数MLE的渐近有效性①

叶晓晨

(吉林师范大学数学学院，吉林四平 136000)

1 问题的提出

关于泊松分布参数估计已有许多的研究，在文献[1]中研究截尾泊松分布参数的MLE，并给出估计的强相合性和渐近正态性.本文在此基础上，得到MLE的又一大样本性质—渐近有效性.

2 截尾泊松分布参数的MLE

设总体X服从泊松分布P(λ)，其中λ ＞0为参数，抽取简单随机样本 X1，X2，…Xn，设K0＞ 0 是事先给定的常数(阈值)，在试验得到的观测值不是，x1，x2，…xn，而是 x1ΛK0，x2ΛK0，…，xmΛK0，这里aΛb=min{a，b}，这种情况可以看成是截尾试验.本文主要基于截尾样本 x1ΛK0，x2ΛK0，…，xnΛK0，讨论λ的MLE的渐近有效性.

为方便，记 ηi=XiΛK0(i=1，2，…，n)，则η1…ηn是一列独立同分布随机变量，且

对数似然函数为

在[1]中已经证明λ的强相合性，即λ)=1，(λ→ λ，a，s)和渐近正态性，即其中V为渐近方差.下面讨论λ的渐近有效性.

在大样本理论中，估计的有效性是一个重要概念，它刻划了估计收敛于真值的速度，其定义也有好几种，通常称达到C－R下界的渐近正态估计为渐近有效估计[2－3].

用λ0表示未知的真实参数，Θ表示参数空间，假设Θ ={λ，A≤λ≤B}，其中A，B为已知正数，λ0是 Θ 的内点.此外，设 fλ(ηi，δi)=(1－

根据强大数定律有

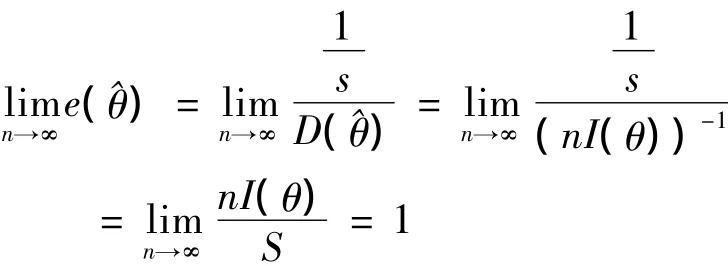
[1]刘银萍，宋立新.II型截尾情形下泊松分布参数的估计[J].吉林大学学报理学版，2007，45(6):941－944.

[2]成平.论极大似然估计的Cramer渐近有效性[J].科学通报，1980，25:1057－1060.

[3]薛红旗，宋立新.分组数据下参数极大似然估计渐近有效性[J].系统科学与数学，2001，21(2);250－256.