填充右左手材料矩形屏蔽微带线色散特性的比较研究

孙 海

（1.乐山师范学院数学与信息科学学院，乐山 614000；2.东华理工大学理学院，南昌 344000）

填充右左手材料矩形屏蔽微带线色散特性的比较研究

孙 海1，2

（1.乐山师范学院数学与信息科学学院，乐山 614000；2.东华理工大学理学院，南昌 344000）

运用矢量有限元法对填充右左手材料的矩形屏蔽微带线的色散特性进行比较研究，包括矩形单信号对称屏蔽微带线，矩形单信号不对称屏蔽微带线，矩形双信号对称屏蔽微带线，矩形双信号位置不对称屏蔽微带线，矩形双信号宽度不对称屏蔽微带线以及矩形双信号厚度不对称屏蔽微带线六种情况.讨论这些屏蔽微带线的主模色散特性随填充材料的变化，色散特性的研究有助于矩形屏蔽微带线和左手材料在新型微波器件中的应用.

色散特性；矢量有限元法；右手材料；左手材料；矩形屏蔽微带线

0 引言

自上世纪四十年代末Cohn［1］开始研究波导的特性以来，对各种波导结构特别是微屏蔽线的研究越来越引起人们的关注.已有的研究表明，微屏蔽线作为一种微波毫米波传输线，具有以下优点：微屏蔽线不需要均衡接地的连接孔（Via-holes）与空气桥（Air-bridge），从而简化了设计制作工艺；屏蔽微带线具有很宽的特性阻抗；屏蔽微带线可以有效地降低与相邻传输线之间的电磁耦合；低交调干扰，易于器件接地连接；屏蔽微带线的金属空腔，既能降低辐射损耗，又因无介质填充而消除了介质损耗.基于诸多特点，屏蔽微带线成为毫米波和亚毫米波波段的主要传输线类型.

对屏蔽微带线的讨论，1991年，Dib与Harokopus等人首先提出了矩形屏蔽微带线，并且用保角变换法分析了特性阻抗［2－3］；随后，Schutt-Aine首次提出了V形屏蔽微带线，且用矩量法计算了特性阻抗［4］；中科院院士林为干先生于1995年首次提出了圆形、椭圆形屏蔽微带线，并利用保角变换法系统地计算了V形、圆形、椭圆形屏蔽微带线的特性阻抗［5－6］；紧接着，Cheng与Robertson研究了非对称V形屏蔽微带线的特性阻抗［7］；Kiang利用点匹配法计算了多种复杂横截面屏蔽微带线的特性阻抗［8］；Yan与Pramanick在前人工作的基础上，提出了一般化的V形与W形屏蔽微带线，计算了特性阻抗与导体损耗［9］；2006年Guney和Robert等人发展了V形屏蔽微带线和微矩形同轴传输线［10－11］，2011年和2012年孙海等分别对椭圆形屏蔽微带线［12］和梯形屏蔽微带线［13］的部分传输特性进行了讨论.

前面的研究极大地丰富了屏蔽微带线的应用，但对填充右、左手材料的矩形屏蔽微带线的主模色散特性研究未见报道；基于此，本文运用矢量有限元方法对填充右手材料和左手材料的多种矩形屏蔽微带线的主模色散特性进行比较研究，具体包括：矩形单信号对称屏蔽微带线，矩形单信号不对称屏蔽微带线，矩形双信号对称屏蔽微带线，矩形双信号位置不对称屏蔽微带线，矩形双信号宽度不对称屏蔽微带线以及矩形双信号厚度不对称屏蔽微带线.六种情况的横截面示意图如图1.

1 原理

横截面示意图1中，中间虚线填充部分为填充介质区域，填充介质的介电常数和磁导率分布为εr和μr，

图1 六种矩形屏蔽微带线横截面示意图Fig.1 Cross-sections of six types of rectangle-shaped microshield lines

白色部分为真空区域，真空的介电常数和磁导率分别为ε0和μ0，而黑色部分表示金属信号线，信号线的尺寸和位置由b／a，b1／a，b2／a，c2／a，c3／a和t／h1，t1／h1，t2／h1控制，填充区域由c1／a控制，并假设h1／a＝0.3，h2／a＝0.2．

使用矢量有限元方法对矩形屏蔽微带线进行讨论，根据Maxwell方程，矩形屏蔽微带线中电场E与磁场H满足以下矢量微分方程

利用电场E的矢量Helmholtz方程推导求解矩形屏蔽微带线色散特性的矢量有限元公式.将式（1）的H代入式（2），得到基于电场E的矢量Helmholtz方程

在矩形屏蔽微带线中，电场E满足矢量微分方程（3）式，及边界条件

经过推导，上述问题等效于下列变分问题

上式中

上式中的δkj用下式进行计算

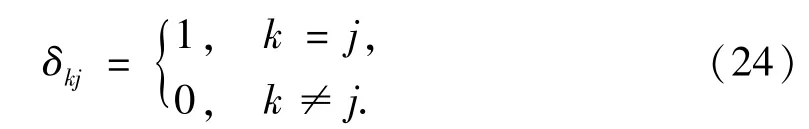
在计算过程中，涉及到形如k1，k2由下标k决定；j1，j2由下标j决定；i1，i2由下标i决定，实际为边所对应的起点和终点.其决定的方式由表1来确定.

利用里兹方法对（7）式进行变分，整理可以得到

表1 三角形单元中棱边与节点之间的关系Table 1 Relation between edge and node in triangular elements

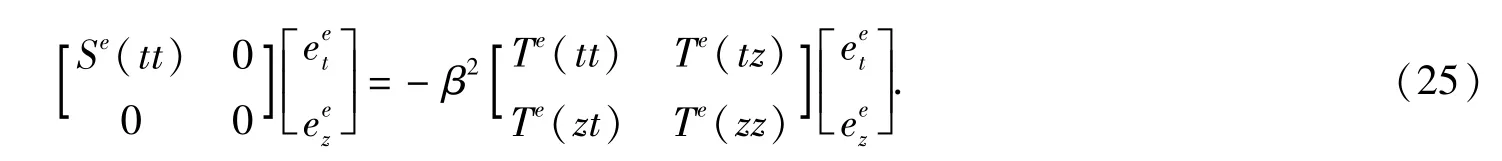
同理，将所有离散的三角形单元的矩阵方程进行合成，可以得到总矩阵方程，即特征值方程：

式（26）中的矩阵［S］和［T］均为方阵，且都是稀疏矩阵，式中β表示待求的特征值，在计算过程中，只要给出k0的取值，就可以求解这个方程.即可以通过求解（26）得到矩形屏蔽微带线的色散特性.

2 数值计算结果

2.1 色散特性的矢量有限元公式的验证

为了验证所使用的矢量有限元公式的正确性和程序的可靠性，首先通过公式（26）求解了半填充波导的色散特性，计算结果如图2所示.

通过图2可以得出，本文的计算结果和相关文献的结果吻合得很好，说明本文所推导的矢量有限元计算公式和所编写的程序是可靠和可行的.下面运用以电场为工作变量的矢量有限元公式对六种矩形屏蔽微带线的色散特性进行计算.在计算过程中，分两组进行讨论：第一组为两种单信号矩形屏蔽微带线；第二组为四种双信号矩形屏蔽微带线；主要进行填充右、左手材料后色散特性的比较，同时也进行两种单信号线和四种双信号线内部的比较.

2.2 矩形单信号屏蔽微带线的色散特性

1）矩形单信号对称屏蔽微带线的色散特性

设c／a＝0.5，c1／a＝0.25，b／a＝0.1，t2／a＝0.1，c2／a＝0.2，且信号线位于模型正中央.

由图3可以得出，当填充的右手材料和左手材料的折射率相同时，填充左手材料后的色散特性和填充右手材料的变化趋势相似；而取相同的k0，填充左手材料的屏蔽微带线比填充右手材料的屏蔽微带线的β值要小.

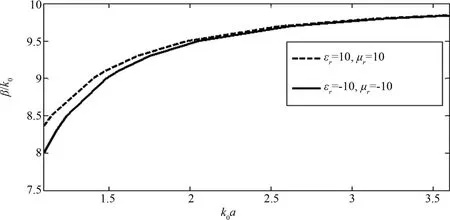
图3 填充右左手材料的矩形单信号对称屏蔽微带线的色散曲线Fig.3 Dispersions of rectangle-shaped microshield line with symmetrical single signal line loaded with right-handed materials and left-handed materials

2）矩形单信号不对称屏蔽微带线的色散特性

下面讨论矩形单信号不对称屏蔽微带线的色散特性，设计尺寸为c／a＝0.5，c1／a＝0.25，b／a＝0.1，t2／a＝0.1，c2／a＝0.05，填充右左手材料后的色散特性如图4.

由图4知，对于填充相同折射率的右、左手材料后，矩形单信号不对称屏蔽微带线的色散特性的变化趋势和矩形单信号对称屏蔽微带线相似.

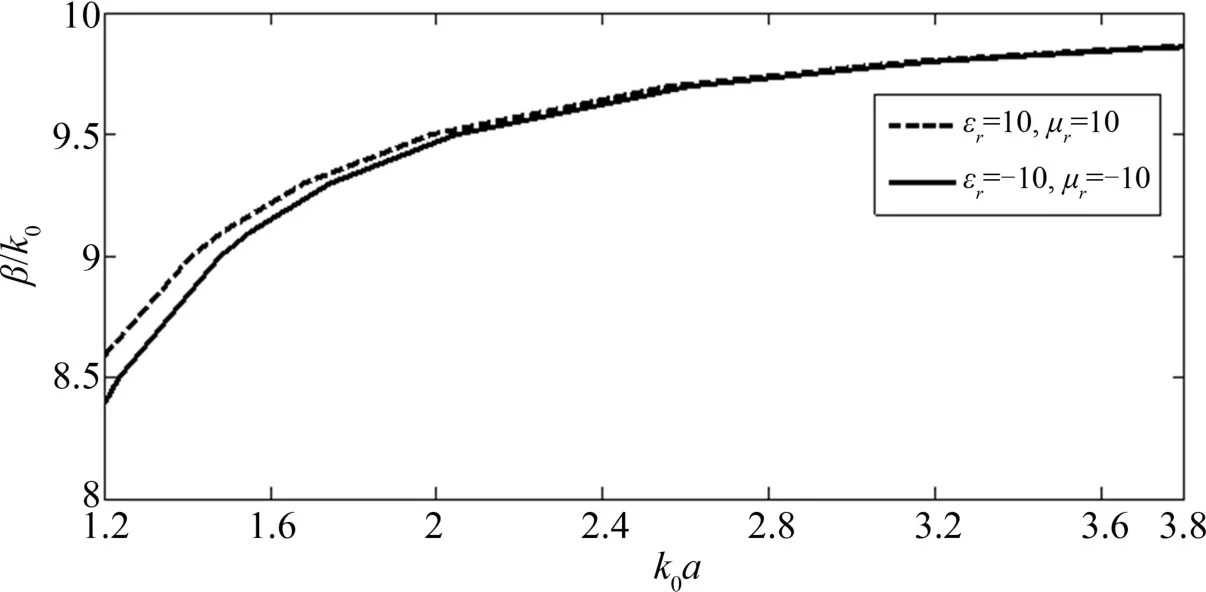
图4 填充右左手材料的矩形单信号不对称屏蔽微带线的色散曲线Fig.4 Dispersions of rectangle-shaped microshield line with asymmetrical single signal line loaded with right-handed materials and left-handed materials

根据上面两个实例的计算得出了几乎相似的结论，故在后面矩形双信号屏蔽微带线色散特性的讨论中，不再讨论同一种信号线随填充材料的变化而引起的色散特性变化；而是重点去比较四种双信号线的色散特性差别.在此之前，先比较两种单信号线色散特性的差别.

3）两种矩形单信号屏蔽微带线色散特性的差别

设矩形单信号对称屏蔽微带线的尺寸为c／a＝0.5，c1／a＝0.25，b／a＝0.1，t2／a＝0.1，c2／a＝0.2，而矩形单信号不对称屏蔽微带线的尺寸为c／a＝0.5，c1／a＝0.25，b／a＝0.1，t2／a＝0.1，c2／a＝0.05，即两种单信号屏蔽微带线除了两信号间的距离不同以外，其他尺寸都相同.填充三种材料（εr＝1，μr＝1；εr＝10，μr＝1；εr＝－10，μr＝－10）后的色散特性比较如图5～图7所示.

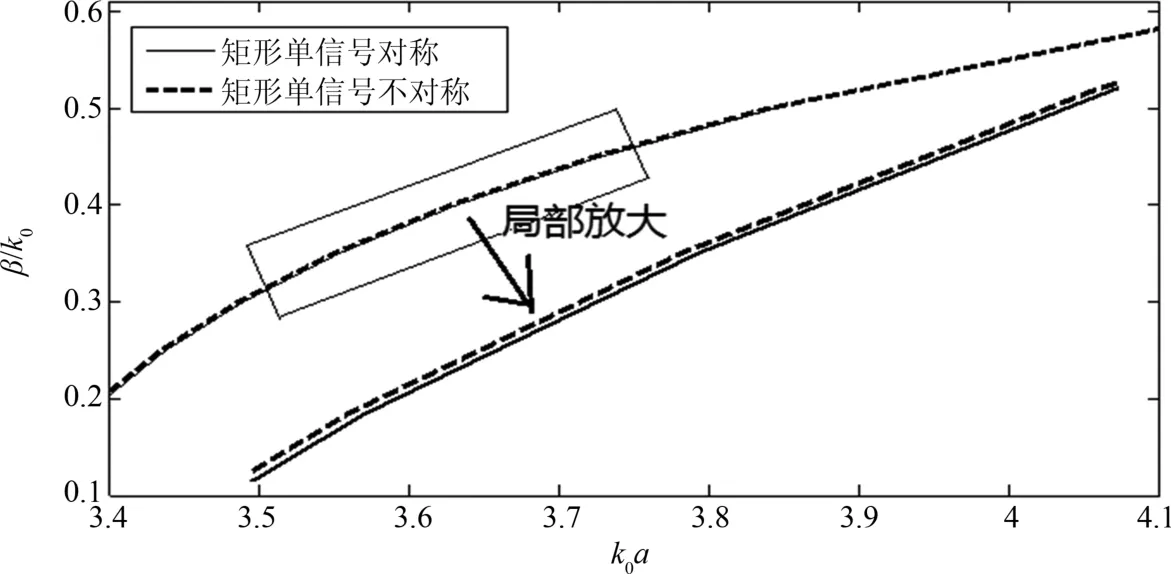
图5 填充εr＝1，μr＝1后两种矩形单信号屏蔽微带线色散特性Fig.5 Dispersions of two kinds of rectangle-shaped microshield line with single signal line loaded with εr＝1，μr＝1

由图5～图7可以看出：无论填充右手材料还是左手材料，矩形单信号对称屏蔽微带线和矩形单信号不对称屏蔽微带线的色散特性差距不大；也就是说在这种情形下，右手材料和左手材料的特性相似.如果要找出两种信号线色散特性之间的细微差别的话，当填充的材料εr＝10，μr＝1时，相比填充其它两种材料（εr＝1，μr＝1；εr＝－10，μr＝－10），两种屏蔽微带线色散特性间的差距稍大一些.

2.3 四种矩形双信号屏蔽微带线色散特性的差别

将MIKE11水动力模块与水质模块进行耦合，模拟计算水库运行期间典型枯水年南碧河水质变化情况，选取南木老河与南碧河交汇口断面、芒片河与南碧河交汇口断面、入小黑江汇口断面3个代表断面进行对比分析，各断面水质预测结果如表2，表3和图2。

这里将对矩形双信号线的四种情况在填充右、左手材料后的色散特性进行比较.这其中包括：双信号线对称，双信号线位置不对称，双信号宽度不对称以及双信号线厚度不对称四种情况.

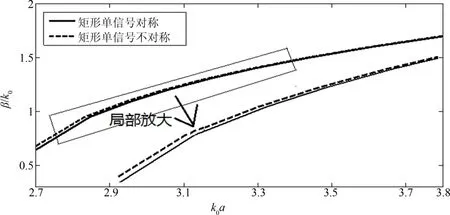
图6 填充εr＝10，μr＝1后两种矩形单信号屏蔽微带线色散特性Fig.6 Dispersions of two kinds of rectangle-shaped microshield line with single signal line loaded with εr＝10，μr＝1

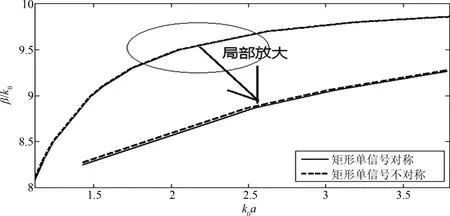
图7 填充εr＝－10，μr＝－10后两种矩形单信号屏蔽微带线色散特性Fig.7 Dispersions of two kinds of rectangle-shaped microshield line with single signal line loaded with εr＝－10，μr＝－10

首先作以下总体假设，假设c／a＝0.5，c1／a＝0.25，c3／a＝0.05，且左侧信号线的宽度和厚度均为0.1.而右侧信号线的尺寸以及位置根据四种不同情况分别定义：

1）双信号对称线为：为了保证对称性，两信号线间的距离为c2／a＝0.2，右侧信号线的宽度和厚度与左侧的一样均为0.1；

2）双信号位置不对称线：右侧信号线的宽度和厚度仍然定义为0.1，两信号线间的距离为c2／a＝0.05；

3）双信号宽度不对称线：两信号线间的距离为c2／a＝0.05，右侧信号线的厚度仍为0.1，而宽度定义为0.2；

4）双信号厚度不对称线：两信号线间的距离为c2／a＝0.2，右侧信号线的宽度仍定义为0.1，而厚度为0.2.

由图8可以得出：当填充的材料为εr＝1，μr＝1，即为均匀传输线时，β的排列顺序为：“厚度不对称”＞“宽度不对称”＞“位置不对称”≈“对称”；且相比之下，“厚度不对称”的β值大得较多.

由图9可以得出：当填充的材料为εr＝10，μr＝1时，β最大的还是“厚度不对称”情况，而且大得很多；相比“位置不对称”和“对称”情况，当k0较小时，“宽度不对称”的β值较大；但随着k0的增加，四种情况的β值几乎没有差别.

由图10和图11可以得出：当填充材料为左手材料εr＝－10，μr＝－10和右手材料εr＝10，μr＝10后，即材料的折射率较大时，无论右左手材料，矩形双信号屏蔽微带线的四种情况的色散特性相差无几.

由图8～图11，得出综合结论：在填充右手材料时，当材料的折射率较小时，在相同的k0下，矩形双信号线的“厚度不对称”和“宽度不对称”的β值比“位置不对称”和“对称”要大很多，究其原因，相比“位置对称”和“位置不对称”，信号线的宽度和厚度增加了，信号线所占的面积也增加了，说明其色散特性与信号线所占

图8 填充εr＝1，μr＝1后四种矩形双信号屏蔽微带线色散特性Fig.8 Dispersions of four kinds of rectangle-shaped microshield line with dual signal lines loaded with εr＝1，μr＝1

图9 填充εr＝10，μr＝1后四种矩形双信号屏蔽微带线色散特性Fig.9 Dispersions of four kinds of rectangle-shaped microshield line with dual signal lines loaded with εr＝10，μr＝1

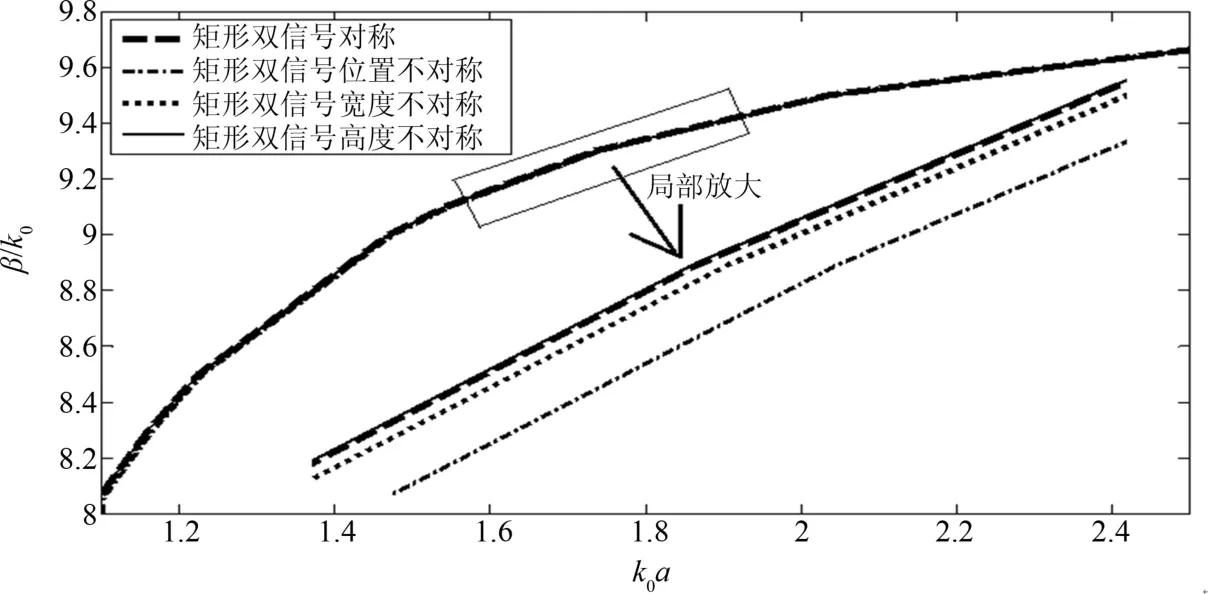
图10 填充εr＝－10，μr＝－10后四种矩形双信号屏蔽微带线色散特性Fig.10 Dispersions of four kinds of rectangle-shaped microshield line with dual signal lines loaded with εr＝－10，μr＝－10

面积有关；但当填充的右手材料折射率较大时，四种矩形双信号屏蔽微带线的色散特性变化不大，这点与填充较大折射率的左手材料的变化规律一致.

3 结语

运用矢量有限元方法对填充右手材料和左手材料的矩形屏蔽微带线六种情况的主模色散特性进行比较

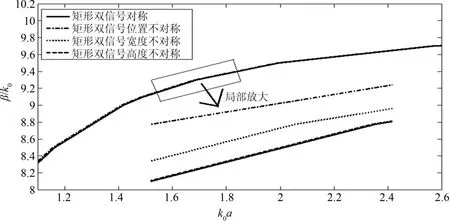
图11 填充εr＝10，μr＝10后四种矩形双信号屏蔽微带线色散特性Fig.11 Dispersions of four kinds of rectangle-shaped microshield line with dual signal lines loaded with εr＝10，μr＝10

研究.计算结果显示，填充左手材料和填充右手材料后，矩形屏蔽微带线的色散特性呈现出不同规律，这对拓展左手材料的应用有重要的实际意义；另外，以信号线个数分组，对单信号的两种情况和双信号的四种情况进行了比较计算，得出了一些有意义的结果，这对矩形屏蔽微带线的进一步发展和应用有指导意义.

［1］Cohn S B.Properties of ridge waveguide［J］.Proc IRE，1974，35（8）：783－788.

［2］Dib N I，Harokopus Jr W P，Katehi P B，Ling C C，Rebeiz G M.Study of a novel planar transmission line［J］.IEEE MTTS International Microwave Symposium Digest，1991：623－626.

［3］Dib N I，Katehi L P B.Impedance calculation for the microshield line［J］.IEEE Microwave and Guided Wave Letters-2，1992：406－408.

［4］Schutt-Aine J E.Static analysis of V-transmission lines［J］.IEEE Transactions on Microwave Theory and Techniques，1992，40（5）：659－664.

［5］Yuan N C，Ruan C L，Lin W G.Analytical analysis of v，elliptic and circular-shaped microshield transmission lines［J］. IEEE Transactions on Microwave Theory and Techniques，1994，42（5）：855－859.

［6］Yuan N C，Ruan C L，Lin W G，He J，He C.Coplanar coupled lines：The effects of the presence of the lateral ground planes，upper and lower ground planes，and the v-shaped microshield ground walls［J］.IEEE Proceedings-Microwaves Antennas and Propagation，1995，142（1）：63－66.

［7］Cheng K K M，Robertson I D.Simple and explicit formulas for the design and analysis of asymmetrical v-shaped microshiled line［J］.IEEE Transactions on Microwave Theory and Techniques，1995，43（10）：2501－2504.

［8］Kiang J F.Characteristic impedance of microshield lines with arbitrary shield cross section［J］.IEEE Transactions on Microwave Theory and Techniques，1998，46（9）：1328－1331.

［9］Yan Y，Pramanick P.Finite-element analysis of generalized v-and w-shaped edge and broadside-edge-coupled shielded microstrip lines on anisotropic medium［J］.IEEE Transactions on Microwave Theory and Techniques，2001，49（9）：1649－1657.

［10］Yidiz C，Kaya S，Guney K，Turkmen M.Neural models for the broadside-coupled v-shaped microshield coplanar waveguides ［J］.International Journal of Infrared and Millimeter Waves，2006，27（9）：1241－1255.

［11］Robert J R，Marsh Eric D，Webster Richard T.Micromachined rectangular-coaxial transmission lines［J］.IEEE Transactions on Microwave Theory and Techniques，2006，54（8）：3433－3442.

［12］Sun H，Wu Y J，Ruan Z S.A study of transmission characteristics in elliptic-shaped microshield lines［J］.Journal of Electromagnetic Waves and Applications，2011，25（17）：2353－2364.

［13］Sun H，Wu Y J.Research on cutoff wavelength of dominant mode and field patterns in trapezoidal-shaped microshield lines ［J］.Turkish Journal of Electrical Engineering＆Computer Sciences，2012，20（4）：463－477.

A Comparative Study on Dispersions of Rectangle-shaped Microshield Lines Loaded with Right-handed Materials and Left-handed Materials

SUN Hai1，2
（1.School of Mathematics and Informational Sciences，Leshan Normal University，Leshan 614000，China；2.School of Science，East China Institute of Technology，Nanchang 344000，China）

Edge-based finite element method is introduced to study dispersions of six types of rectangle-shaped microshield lines loaded with right-handed materials and left-handed materials.They are rectangle-shaped microshield lines with symmetrical single signal line，with asymmetrical single signal line，with symmetrical dual signal lines，with asymmetrical dual signal lines of position，with asymmetrical dual signal lines of width and with asymmetrical dual signal lines of height.Dispersions of microshield lines with changed dielectric constant of dielectric substrate are discussed.Numerical results are helpful in design of microwave components that use rectangle-shaped microshield lines and left-handed materials.

dispersion；edge-based finite element method；right-handed material；left-handed material；rectangle-shaped microshield line

date：2013－10－08；Revised date：2014－02－19

TN81

A

2013－10－08；

2014－02－19

四川省教育厅资助科研项目（14ZB0250）；乐山师范学院博士启动项目（Z1326）及江西省自然科学青年基金项目（20122BAB211008）资助

孙海（1981－），男，理学博士，讲师，主要从事计算电磁学研究，E-mail：sunhai0804＠126.com

1001-246X（2014）05-0593-09