15 eV的质子与羟基碰撞的动力学
朱 云, 张秀梅, 王志萍
(江南大学理学院,无锡 214122)
15 eV的质子与羟基碰撞的动力学
朱 云, 张秀梅, 王志萍
(江南大学理学院,无锡 214122)
采用含时密度泛函理论和分子动力学非绝热自洽耦合的方法,全微观研究沿垂直羟基分子轴向入射初动能为15 eV的质子与羟基碰撞过程的电子-离子关联动力学.计算质子和羟基动能、碰撞后羟基电子和离子的运动状态及系统电子密度的实时分布.结果表明:质子与羟基碰撞后俘获羟基的一部分电子被反弹并损失26.7%的初始动能而羟基动能增加.碰撞后丢失1%电子的羟基在保持碰撞前收缩振动的同时向计算边界平动并以93%的中性和7%的+1价的几率存在.
含时密度泛函;分子动力学;羟基;碰撞
0 引言
原子、分子、离子间的碰撞反应是复杂的动态物理过程,是存在于天体物理、大气物理、大气化学、化学反应中最普遍的物理、化学现象之一[1-4].随着粒子束技术的广泛应用,人们对重粒子碰撞过程的研究兴趣日益增加,例如在核裂变反应堆、粒子束刻印术等应用方面,都涉及到重粒子碰撞中包含的激发、电离以及电荷转移等过程.质子是最简单的离子.在过去的几十年里,在许多领域,比如加速器、材料科学、等离子体、天体物理等领域质子与分子的碰撞研究已经获得了人们的高度重视[5-6].同时,21世纪是生命科学的世纪,生命物质和生命现象已成为科学家研究的重要对象,离子辐照育种、质子和重离子治癌成为科学的前沿[7].在理论上,从分子和细胞水平上研究生物体的电离辐射损伤是辐射生物学与放射医学的基础,是涉及原子核物理、生物、化学和医学等学科交叉的一个重要的前沿领域.生物分子损伤是一切辐射生物效应的物质基础.而生物分子损伤与自由基生成密切相关.羟基是一种重要的活性氧氢键,由于其化学性质比较活泼,生物体的嘌呤碱基和嘧啶碱基就成为羟基攻击的主要目标,最终导致碱基的变异、DNA链的断裂及DNA的损伤等[8-9].但是关于生物体内大量存在的质子与羟基碰撞的反应动力学的研究目前报道很少.本文采用含时密度泛函理论和分子动力学非绝热耦合的方法(TDDFT-MD)[10-11]研究初动能为15 eV的质子沿垂直羟基分子轴向入射与羟基碰撞的反应动力学.质子、羟基参与生命活动的过程是非常复杂的,本文以最简单的质子和羟基为研究对象,寻找其碰撞反应动力学规律对于研究复杂生物体系的辐射生物效应有重要的指导意义.
1 模型与计算方法
在TDDFT-MD方法中,在外场作用下的原子或分子系统可以看成是由外场、价电子和离子实三部分组成.一个多原子分子的能量E包括离子之间的相互作用能量Eion、电子之间的相互作用能量Eel及离子与电子之间的相互作用能量Ecoup,即

其中,Ekin,ion和Epot,ion分别表示离子动能和离子间的库仑相互作用势能;Ekin,el为电子动能;EC是电子库仑能;Exc表示电子的交换关联势;ESIC为自洽相互作用修正项;EPsP为赝势,其中还包含了非局域的部分;Eext表示外场.
含时密度泛函理论(time dependent density functional theory,TDDFT)[12]用来描绘系统成键或者价电子的含时行为,而离子实作为经典的离子用标准的分子动力学来描述.TDDFT的主要物理思想就是在构造N个电子相互作用系统的运动方程时,以空间和时间相关的密度n(r,t)为自变量.使用原子单位me=e=ħ =1,根据Kohn-Sham定理[12],无相互作用的单粒子波函数φj(r,t)满足含时Kohn-Sham(TDKS)方程为
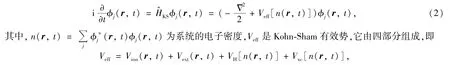
其中Vion(r,t)为离子的背景势,采用模守恒赝势.在对多原子分子的计算中,赝势的具体形式采用了Goedecker等人[13]的形式,其中包含了局域部分和非局域部分.对于给定的单粒子波函数φj(r),有
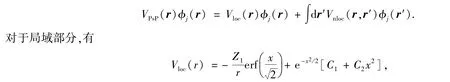
其中erf为误差函数,Z1为离子的电荷数.x=r/rloc,rloc是高斯电荷分布半径.对于非局域部分,有
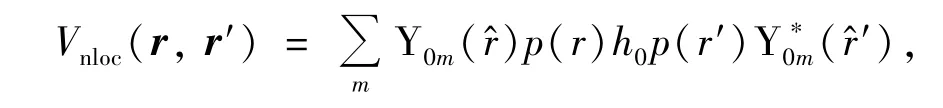


2 结果与讨论
羟基共有2个离子和7个共价电子.在计算过程中,羟基位于x轴上,羟基中氧原子在坐标原点,氢原子在氧原子的右侧.基态计算所得的羟基的键长及电离能分别为1.82a0和14.01 eV,与实验值1.83a0和13.02 eV[18]的相对误差分别为0.55%和7.6%.这表明羟基的基态结构与实验值是比较符合的.计算采取正方体空间,大小为64a0×64a0×64a0.在质子与羟基碰撞的演化过程中,计算采用相同的时间步长Δt=0.012 5a.u..计算边界采用吸收型边界条件,三个方向上的吸收边界宽度为4a0.计算空间采用的网格大小为0.412a0.图1为质子沿y轴入射(即沿垂直羟基分子轴向入射)与羟基碰撞结构示意图.具体计算过程中,质子是以15 eV的初动能从初始位置(b,12a0,0)出发沿y轴负向入射的,其中b表示的是碰撞参数,即改变碰撞参数b时,质子是沿羟基的分子轴向变化位置的.
图2给出的是质子与羟基在x方向、y方向坐标随时间变化(z方向质子和羟基基本保持不动).图3为质子动能损失及羟基动能随时间变化.首先,对于质子,由图2 (b)可以看出质子在大约10 fs的时候最靠近羟基分子,之后在y方向被反弹.而在x轴方向,一开始质子的坐标为零.碰撞后,质子则以一定的速度向x轴负方向移动.对于质子动能的变化,由图3(a)可以看出,在质子逐渐接近羟基并与羟基发生碰撞并反弹的整个过程中,质子的动能由于长程相互作用在原有的基础上先急剧增加7 eV,之后又迅速减少16 eV,最终在17 fs左右质子的动能达到新的稳定值,但其动能与初动能相比损失了4 eV,即损失了26.7%的初始动能.其次,对于羟基分子,由图2可以看出,在质子最接近之前(即前10 fs),氧原子基本保持不动,而氢原子在x方向有小幅振动,这表明在碰撞前羟基在xy平面内沿分子轴向做伸缩运动.在碰撞发生后,氧原子以恒定的速率向y轴负方向运动,而氢原子围绕氧原子在x、y方向都有运动,这表明羟基与质子发生碰撞后,除了做伸缩振动外,还获得了平动动能,逐渐向计算边界运动.对于羟基动能的变化,由图3(b)可以发现,在质子最接近前,羟基分子的动能很小,这表明羟基做微弱的伸缩运动.在质子最接近时,羟基的动能迅速增加至4.3 eV,之后在3.4 eV附近上下波动.这与图2中羟基碰撞后除了有振动外还有平动是相吻合的.综合图2和图3可以得出,质子以15 eV的初动能沿垂直羟基分子轴向入射情况下,碰撞后质子被反弹且动能减小;羟基在原来伸缩振动的基础上又发生平动,动能增加且伸缩振动变强.
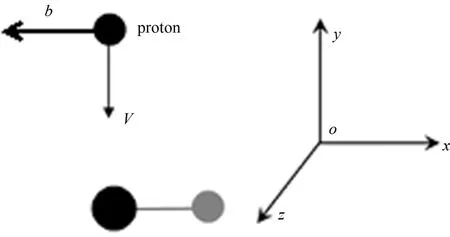
图1 质子沿y轴入射与羟基碰撞的示意图Fig.1 Schematic of collision between a y-axis incident proton and a hydroxyl
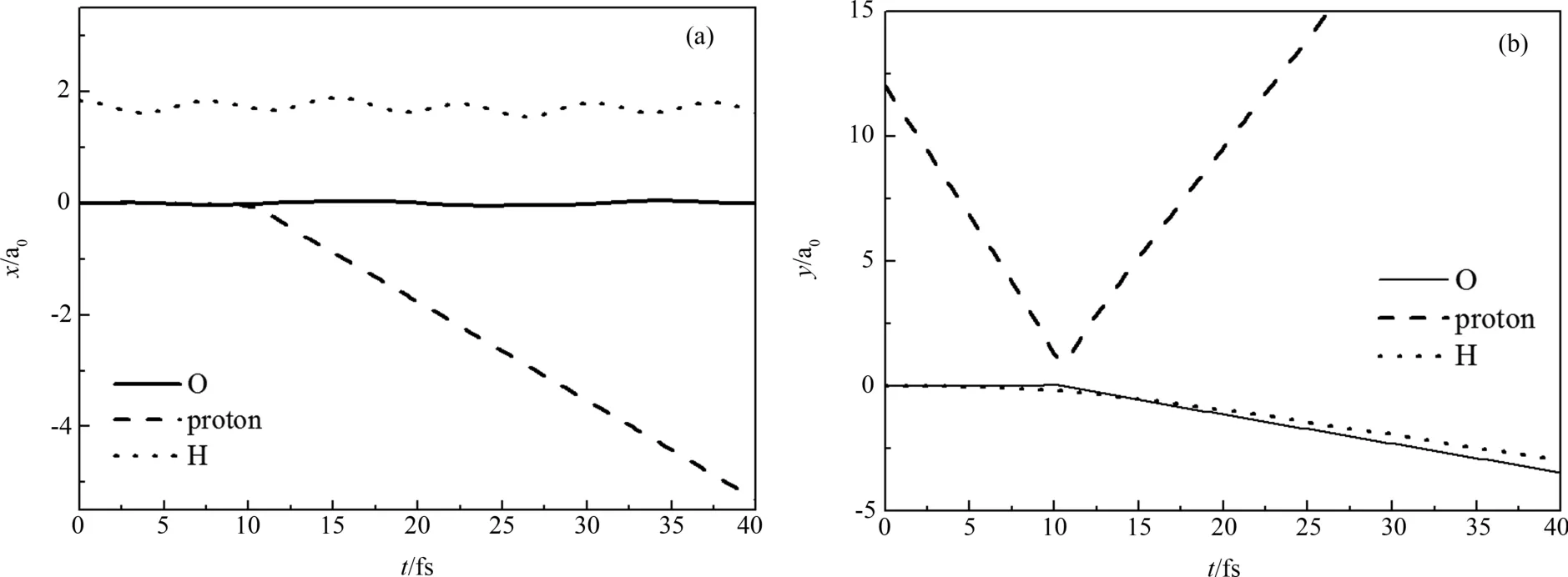
图2 质子与羟基在x方向、y方向坐标随时间变化Fig.2 Time evolution of coordinates of proton and hydroxyl in x and y directions

图3 质子及羟基动能变化随时间变化Fig.3 Time evolution of kinetic energies of proton and hydroxyl
图4(a)为羟基电离随时间变化关系.由图4(a)可以看出羟基在前17 fs内几乎没有电子被电离.在17 fs至20 fs内电离迅速增加并逐渐趋于饱和,在40 fs时大约有0.07个电子被电离,即大约有1%的电离.图4(b)给出了碰撞前后羟基各电荷态几率随时间变化.由图4(b)可以发现,在前17 fs内,由于没有电离,所以羟基分子是以中性分子存在的.之后,由于电离,中性羟基分子的几率降低,P(1+)增加,这表明羟基以+1价形式存在的几率增加而且羟基以其他价态形式存在的几率为零.最终羟基以93%的中性和7%的+1价的几率存在.

图4 羟基电离及各电荷态几率随时间变化Fig.4 Time evolution of ionization and charge state probability of hydroxyl
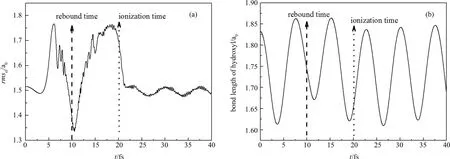
图5 羟基电子均方根半径及羟基键长随时间变化Fig.5 Time evolution of electronic root mean square radius and bond length of hydroxyl
图5给出了羟基电子均方根半径及羟基键长随时间变化.为了形象的说明碰撞过程中的典型时刻,图5中分别用带箭头的红色虚线和蓝色点线表示质子反弹及系统电离发生的时刻.电子的均方根半径可以给出电子在整个计算空间的弥散程度.由图5(a)可以看出,rmsel的初始值为1.52 a0.在前10 fs内,rmsel先陡然增大然后又迅速减小,这是由于在质子逐渐接近羟基时(10 fs是质子最接近羟基的时刻)长程相互作用导致电子弥散先增大后减小.这与图2中碰撞发生的时刻及图3(a)中质子动能损失的变化趋势是相吻合的.在10 fs至20 fs内,rmsel又迅速增大,这表明电子弥散得更开.这主要是由于质子被反弹而俘获羟基的一部分电子导致的(但整个系统这个时间段内没有电离).之后在20 fs左右,rmsel又迅速降低,这是由于质子运动至计算边界处,被质子俘获的电子被吸收边界条件吸收,从而导致电子弥散程度变小,这与图4(a)中在大约20 fs时,羟基电离陡然增强是相吻合的.之后,rmsel做周期约为7.5 fs的小振幅振荡.对于整个碰撞过程中羟基的键长变化,由图5(b)可以发现,碰撞前后羟基的键长都作振荡而没有断裂.这与图3和图4得到的羟基做收缩振动是相吻合的.此外,不难发现在20 fs以后羟基键长振动的周期约为7.5 fs,这与图5(a)中20 fs以后rmsel振动的周期是吻合的,这表明羟基剩余的电子与离子的运动耦合的很好.
电子局域化函数(ELF)能够用来描述分子和固体中化学键的形成[19-20].最近,Burnus等人[21]发展了时间相关的电子局域化函数用来分析化学键的成键与断裂.图6形象地给出了不同时刻二维的在xy平面内的羟基电子密度分布相对其基态电子密度分布的变化.图6中左上角的子图为羟基在xy平面的基态电子密度分布的等高线图.子图按顺时针排序为时间逐渐增大的顺序.对于羟基基态的电子密度,从图6左上角子图可以看出羟基处于基态时电子集中分布在原子的周围,这表明电子与原子耦合的很好而且计算空间是足够大的.顺时针观察图6中各子图可以发现,当质子逐渐靠近羟基的过程中质子俘获一部分电子并反弹,当质子运动至边界时被质子俘获的电子被吸收,导致系统电离增大.

图6 不同时刻羟基在xy平面的电子密度分布相对其基态电子密度分布变化的等高线图及原子结构示意图Fig.6 Contour plots of electron localization and ionic structures of hydroxyl in xy plane at different moment
图7为15 eV质子与羟基碰撞过程中羟基电离的加权概率与碰撞参数的关系.对比图7和Sidky等人[22]计算得到的50 eV质子与氢原子碰撞的电离加权概率与碰撞参数的关系图,可以发现两者曲线变化趋势相近.由图7可以看出当碰撞参数从0 a0增加至1 a0过程中,bP(b)缓慢增加.当碰撞参数从1 a0增加至2.5 a0过程中,bP(b)先陡然增大又迅速降低至零附近,其中在b=1.5a0时bP(b)达到峰值.通过计算发现在当前条件下质子与羟基碰撞的电离截面σICS=0.127 4 Å2.该值与Kim[23]等人采用BEB理论计算得到的15 eV电子与水分子碰撞的电离截面σBEB=0.122 Å2非常接近.此外,提高入射质子的初动能,计算发现,当入射质子的初动能分别为250 eV、25 KeV情况下质子与羟基碰撞的电离截面值分别为σICS=0.509 1 Å2和σICS=1.299 0 Å2.后者与Coupier[24]等人实验得到的25 KeV质子与水分子碰撞的电离截面3 Å2相近.
3 结论
采用含时密度泛函理论和分子动力学非绝热自洽耦合的方法,从全微观的角度研究了15 eV的质子沿垂直羟基分子轴向入射与羟基碰撞的电子-离子关联动力学.计算了质子的能量损失、碰撞后羟基电子和离子的运动状态及电子密度的实时分布.研究表明,质子与羟基碰撞后俘获羟基的一部分电子被反弹并损失了26.7%的初始动能而羟基动能增加.碰撞后有1%电离的羟基保持收缩振动运动状态的同时向计算边界移动并以93%的中性和7%的+1价的几率存在.通过对电离截面的计算发现15 eV的质子与羟基碰撞的电离截面与BEB理论计算所得15 eV电子与水分子碰撞的电离截面相当,25 KeV的质子与羟基碰撞的电离截面与25 KeV的质子与水分子碰撞的电离截面相近.
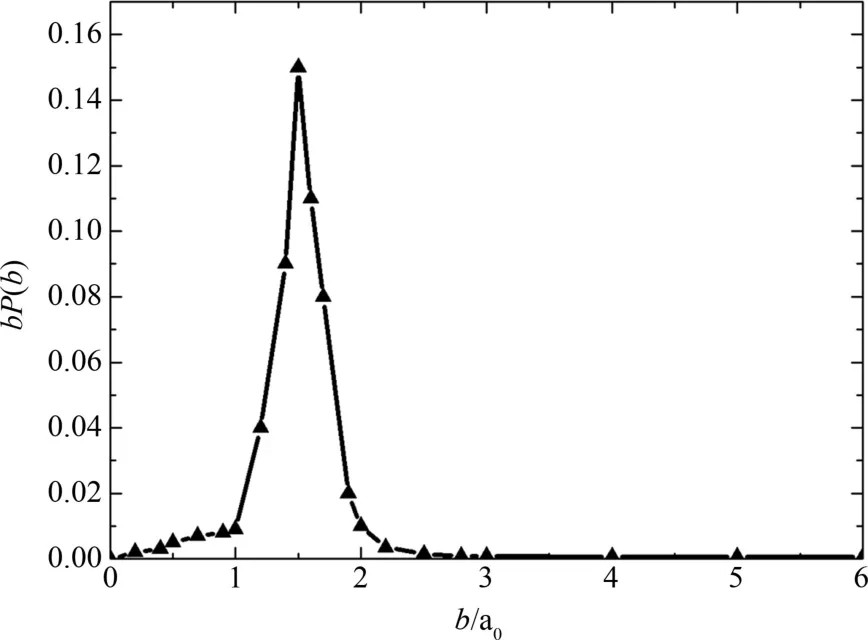
图7 15 eV质子与羟基碰撞过程中羟基电离的加权概率与碰撞参数关系Fig.7 Weighted probabilities of ionization of hydroxyl in a collision with 15 eV proton
[1]Krasnopolsky V A,Mumma M J.Spectroscopy of comet Hyakutake at 80~700 Å:First detection of solar wind charge transfer emissions[J].Astrophys J,2001,549(1):629-634.
[2]Luna H,Montenegro E C.Fragmentation of water by heavy ions[J].Phys Rev Lett,2005,94(4):043201-1-043201-4.
[3]Melo W S,Santos A C F,Sant'Anna,et al.Dissociative and non-dissociative ionization of the N2molecule by the impact of 0.75~3.5 MeV He+[J].J Phys B,2006,39(17):3519-3528.
[4]Bacchus-Montabonel M C,Tergiman Y S,Talbi D.Ab initio molecular treatment of charge-transfer processes induced by collision of carbon ions with 5-halouracil molecules[J].Phys Rev A,2009,79(1):012710-1-012710-7.
[5]Stopera C,Maiti B,Grimes T V,et al.Dynamics of H++CO at ELab=30 eV[J].J Chem Phys,2012,136(5):054304-1-054304-13.
[6]Murakami M,Kirchner T,Horbatsch M,et al.Fragmentation of water molecules by proton impact:The role of multiple electron processes[J].Phys Rev A,2012,85(5):052713-1-052713-4.
[7]Mathur D.Multiply charged molecules[J].Phys Rep,1993,225(4):193-272.
[8]Shukla M K,Leszczynski J.A theoretical investigation of excited-state properties of the adenine-uracil base pair[J].J Phys Chem A,2002,106(6):1011-1018.
[9]Von Sonntag C.Free-radical-induced DNA damage and its repair:A chemical perspective[M].New York:Plenum Press,1991.
[10]Calvayrac F,Reinhard P-G,Suraud E,et al.Nonlinear electron dynamics in metal clusters[J].Phys Rep,2000,337(6):493-578.
[11]Fennel T,Meiwes-Broer K-H,Tiggesbáumker J,et al.Laser-driven nonlinear cluster dynamics[J].Rev Mod Phys,2003,82(2):1793-1842.
[12]Gross E K U,Kohn W.Time-dependent density functional theory[J].Adv Quant Chem,1990,21:255-291.
[13]Goedecker S,Teter M,Hutter J.Separable dual-space Gaussian pseudopotentials[J].Phys Rev B,1996,54(3):1703-1710.
[14]Perdew J P,Wang Y.Accurate and simple analytic representation of the electron-gas correlation energy[J].Phys Rev B,1992,45(23):13244-13249.
[15]Legrand C,Suraud E,Reinhard P G.Comparison of self-interaction-corrections for metal clusters[J].J Phys B,2002,35 (4):1115-1128.
[16]UllrichC A.Time-dependent kohn-sham approach to multiple ionization[J].J Mol Str,2000,501-502:315-325.
[17]Gao C Z,Wang J,Zhang F S.Dynamics of proton collisions with acetylene,ethylene and ethane at 30eV[J].Chem Phys,2013,410:9-18.
[18]http://cccbdb.nist.gov/.
[19]Becke A D,Edgecombe K E.A simple measure of electron localization in atomic and molecular systems[J].J Chem Phys,1990,92(9):5397-5403.
[20]Bilalbegovié G.Carbonyl sulphide under strong laser field:Time-dependent density functional theory[J].Eur Phys J D,2008,49(1):43-49.
[21]Burnus T,Marques M A L,Gross E K U.Time-dependent electron localization function[J].Phys Rev A,2005,71(1):010501-1-010501-4.
[22]Sidky E Y,Lin C D.Total cross-section calculations on proton-impact ionization of hydrogen[J].Phys Rev A,2001,65 (1):01711-1-01711-11.
[23]Kim Y K,Rudd M E.Binary-encounter-dipole model for electron-impact ionization[J].Phys Rev A,1994,50(5):3954-3967.
[24]Coupier B,Farizon B,Farizon M,et al.Inelastic interactions of protons and electrons with biologically relevant molecules [J].Eur Phys J D,2002,20(3):459-468.
Collision Dynamics of Hydroxyl and Proton at 15 eV
ZHU Yun,ZHANG Xiumei,WANG Zhiping
(School of Science,Jiangnan University,Wuxi 214122,China)
Under the frame of time-dependent density functional theory(TDDFT)and molecular dynamics,we studied microscopic electronic-ionic association dynamics in collision between hydroxyl and proton which moves toward molecular axis of hydroxyl with 15 eV initial kinetic energy.Energies of projectile and target,electron and vibration excitations of target and real time distribution of electron density are identified.It is found that proton captures electrons of hydroxyl in collision and it rebounds from the target with loss of 26.7%of initial kinetic energy.While the kinetic energy of hydroxyl increases and hydroxyl moves toward to numerical boundary accompanied with stretch oscillation.Hydroxyl loses 1%electrons and exists as neutral and+1 valence forms with 93%and 7% probabilities respectively.
TDDFT;molecular dynamics;hydroxyl;collision
date:2013-07-21;Revised date:2014-02-12
O56
A
2013-07-21;
2014-02-12
中央高校基本科研业务费专项资金(JUSRP 111A21,JUSRP 31005);国家自然科学基金(61178032,11174114)及江南大学校内自主理科专项资金(1142050205135370)资助项目
朱云(1977-),女,江苏无锡,汉族,讲师,主要从事纳米材料的理论研究
王志萍E-mail:zpwang03247@163.com
1001-246X(2014)05-0602-07

