2-2型PMNT/NFO复合磁电效应模拟
杨焕银, 樊冬梅, 郭红力
(长江师范学院凝聚态物理研究所,重庆涪陵 408100)
2-2型PMNT/NFO复合磁电效应模拟
杨焕银, 樊冬梅, 郭红力*
(长江师范学院凝聚态物理研究所,重庆涪陵 408100)
利用弹性力学模型,基于铁电相与铁磁相的本构方程,建立磁电复合材料的本构方程,推导2-2型非理想耦合的磁电双层、三层复合薄膜的纵向、横向磁电(ME)电压系数.研究铁磁相材料铁酸镍(NFO)和铁电相材料铌镁酸铅-钛酸铅(PMNT)复合的磁电效应,分析复合材料的磁电电压系数与PMNT体积分数、界面耦合参数、两相体积比及复合总层数的关系.结果表明两相材料的性能、体积分数以及耦合系数、复合层数都影响磁电电压系数.
磁电效应;耦合;复合材料;本构方程
0 引言
磁电复合材料的磁电效应(ME)是指在外加电场下复合材料发生磁化,或者在外加磁场下发生极化的现象[1].它是一种兼具电磁伸缩性能和电致伸缩性能的特殊材料,是按照一定的复合结构(即通过加和效应或者耦合乘积效应)得到的一种性能远高于单相磁电材料或产生单相材料所没有的磁电效应的新型材料[2].根据复合结构的不同,磁电复合薄膜分为1-3型柱状磁电复合薄膜[3-4],0-3型颗粒磁电复合薄膜[5-7]以及2-2型层状磁电复合薄膜[8].由于磁电复合材料是由铁电相和铁磁相材料构成,而铁电材料必须是绝缘体,铁磁相材料一般是金属,电阻率较低,因此在复合的时候容易出现渗流,且两相在复合的时候存在晶格的位错和畸变,因此铁电和铁磁相复合材料在物理性质、结构特征、电子特性等方面都会受到一定的限制,这说明多铁性的形成是诸多元素竞争的结果.2-2型磁电复合薄膜由铁磁相膜层和铁电相膜层层叠构成.与前两种结构相比,2-2型磁电复合薄膜的最大优点是电阻率很高的铁电相膜层能够完全阻断磁性相膜层之间的连通,使得材料整体的漏电流较小,有利于磁电性能的提高磁电效应为发展新一代高性能的磁电功能器件提供了可能,可以用来制作类型多样的新型磁控或者电控亦或同时磁控-电控器件.除此之外,它还兼具磁致伸缩性和压电性,所以具有较高的介电常数和磁导率,可以用这类材料来制成小型或微型的多功能电磁器件.因此,磁电复合材料正逐渐成为磁电材料研究的热点[9-11].
磁电耦合效应的工作原理可以概括为:外加磁场下磁致伸缩相的变形引发内应力,此应力通过两相间界面传递到铁电相,由于铁电相的受力形变会产生极化,这一极化会在界面上产生表面电荷.磁电复合薄膜制备方面,不同研究者做了大量的工作[12-15].2008年Zhang[12]用PLD方法在SrTiO3单晶基片上沉积了Pb (Zr0.52Ti0.48)O3(PZT)/SrRuO3/CoFe2O4复合薄膜.它以PZT薄膜作为缓冲层,缓解了表面张力,增强了层间界面处的耦合,提高了复合薄膜的磁电耦合性能.同年,Zhong[15]等采用溶胶-凝胶技术在Pt/Ti/SiO2/Si (100)基片上沉积了Bi3.15Nd0.85Ti3O12(BNT)和CoFe2O4(CFO)磁电复合薄膜,根据沉积顺序的不同,分别得到BNT/CFO/基片(BC)和CFO/BNT/基片(CB)薄膜.研究发现,BC薄膜表面平滑致密.而CB复合薄膜的漏电流密度比BC复合薄膜的低,绝缘性较好.同时磁电测试发现,BC复合薄膜和CB复合薄膜的磁电电压系数最大分别为91 mV·cm-1·Oe-1和84 mV·cm-1·Oe-1.不同的沉积方式造成B与C界面的耦合程度不同,造成了致密度较好的CB复合薄膜的磁电性能高于BC复合薄膜.我们实验制备PMNT与CFO多层磁电复合薄膜,发现这种磁电复合薄膜具有较好的铁电和铁磁性能,并且也具有一定的磁电性能[16].目前,人们对于磁电复合材料的实验研究主要集中在钙钛矿结构的含铅铁电相材料(如Pb(Zr0.52Ti0.48)O3(PZT)、Pb (Mg1/3Nb2/3)O3-PbTiO3(PMN-PT)等)和尖晶石结构的铁磁相材料(如CoFe2O4(CFO)、NiFe2O4(NFO)等).层状复合材料的理论模型主要有弹性力学模型[17]、Green函数方法[18]及等效电路模型[19]等.其中弹性力学模型因为其应力-应变机理的解释得到了众多研究者的亲睐.本文以层状磁电复合材料弹性力学模型为基础,建立铁电-铁磁相本构方程,对PMN-PT/NFO非理想层间耦合的双层和三层复合薄膜磁电效应进行研究.讨论两相体积比、层间耦合系数以及薄膜层数对复合磁电薄膜磁电性能的影响,为磁电复合薄膜实验研究提供进一步的指导.
1 理论模型
图1是我们研究的磁电双层和三层薄膜的结构示意图.坐标系的1,2轴位于平面内,3轴表示沿薄膜的厚度方向.为了测量双层膜的动态磁电效应,这里定义ME电压系数αE=δE/δH,并有两种不同的磁场方向.横向ME电压系数αE,31=δE3/δH1对应偏置磁场H交变磁场δH互相平行且沿1轴,沿厚度方向测量产生的交变电场δE.纵向ME电压系数αE,33=δE3/δH3对应于三个场,它们互相平行且皆沿3轴.
根据铁电相和铁磁相的本构方程,复合磁电薄膜的本构方程可表示为[20]
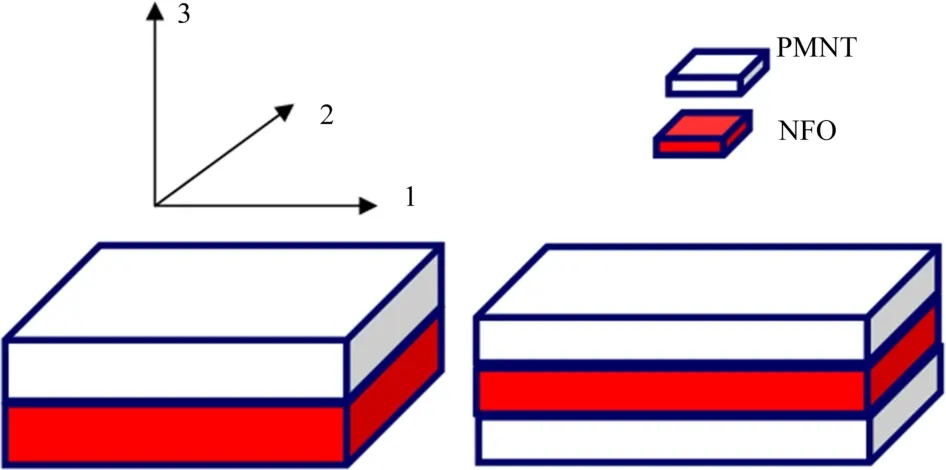
图1 层状磁电复合薄膜结构示意图Fig.1 Schematic illustration of magnetoelectric laminated compsite films
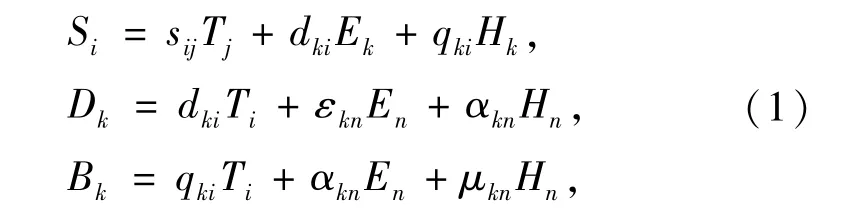
式中i,j,k=1,2,3,代表了坐标轴的三个方向.S,T分别为二阶应变、应力张量;E,D,H,B分别为电场,电位移,磁场,磁感应强度矢量;sij,dki,qki分别为有效柔顺系数,压电系数和压磁系数;εkn,μkn,αkn分别为有效介电常数,磁导率和磁电电压系数.
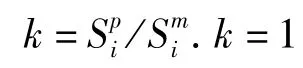

式中,上角标p,m分别代表压电相、压磁相材料,v为压电相所占薄膜体积的体积分数(v=vp/(vm+vp)).其中第一部分指的是理想情况下衬底与压电薄膜在横向和纵向上的应变相等;第二和第三部分是指在沿轴1和2的方向上总的力矢为零.
由上述本征方程(1)及边界条件(2),可得出横向和纵向ME电压系数的表达式
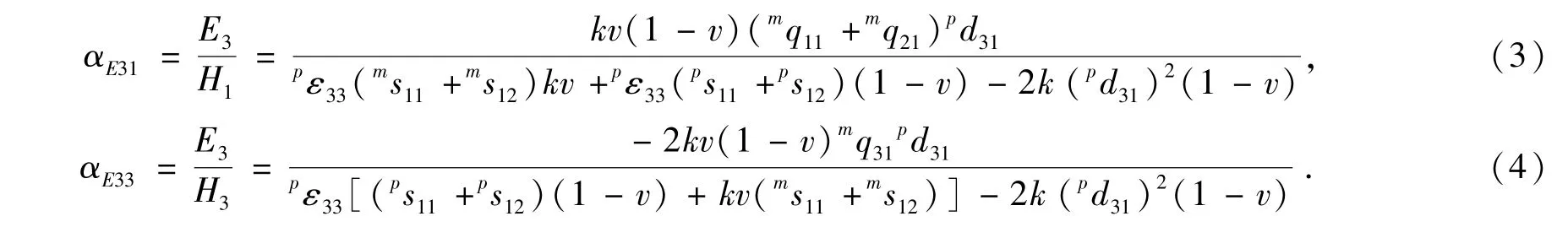
同样对于三层磁电复合薄膜材料,我们也可以利用上面的结论研究三层复合薄膜材料的ME电压系数.对于三层薄膜中的压电相占整个复合薄膜材料的体积分数为
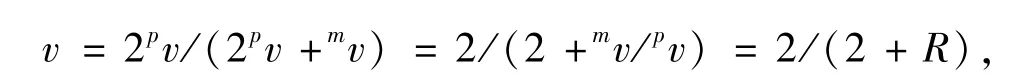
其中R=mv/pv,表示压磁相与压电相的体积比.将其带入方程(3),横向ME电压系数αE31随两相体积比R变化的表达式为
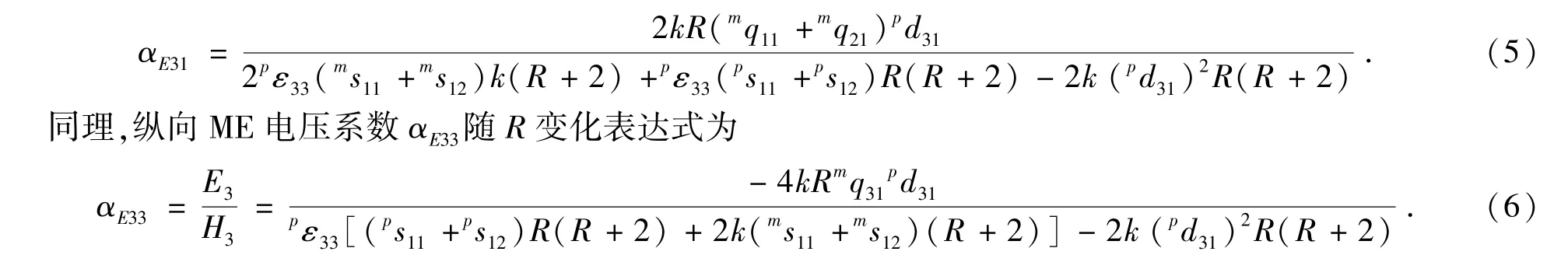
影响磁电复合材料ME电压系数的最根本的原因就是复合界面的耦合程度,即层间耦合系数.而层间耦合系数的大小又强烈地依赖于复合薄膜的层数.通过利用NiFe2O4-Pb(Zr,Ti)O3得到的磁电耦合经验公式[21-22]

其中n为磁电复合薄膜总层数.将方程(7)带入(3)、(4),即可研究不同复合薄膜层数n对PMNT/NFO复合的磁电耦合效应.
2 结果和分析
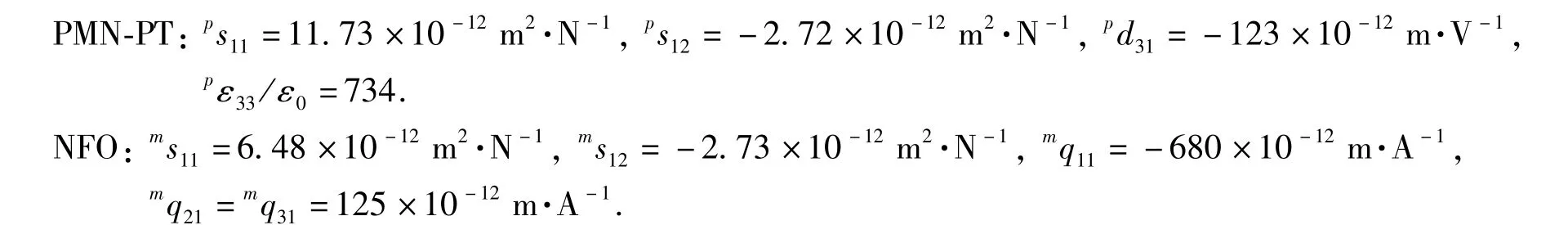
在弹性力学模型基础上,我们研究PMNT/NFO复合的磁电耦合效应,以下为相应材料的电学、磁学及力学参数[23-25].两相复合磁电材料的磁电耦合性能受到诸多因素的影响,如两相体积比、层间耦合系数等因素的影响等.图2 为PMNT与NFO复合得到的横向和纵向ME电压系数与PMNT体积分数v之间的关系曲线.首先,从图2可以看到,PMNT体积分数v等于0或者1时复合材料无磁电效应,即单相材料不产生磁电效应.随着v的不断增加,横向、纵向ME电压系数的值先不断增加达到一个峰值,再逐渐减小至零,在某一vmax值时存在一个ME效应的最大值.对比横向和纵向ME电压系数峰值,发现界面耦合状态一样的情况下(即k值相同),横向磁电电压系数αE31要比纵向的磁电电压系数αE33要大接近一倍,这说明复合材料在水平方向的压磁效应强于垂直方向.这种现象已经在众多的实验中得到验证,说明异质结构的复合薄膜在结构和外延制备上存在各向异性[26].此外,随着界面耦合系数k的逐渐减小,ME耦合逐渐也逐渐变弱,ME电压系数数值发生锐减,其ME电压系数的峰值所对应的PMNT体积分数vmax逐渐向富含铁电相的区域偏移.以横向ME磁电效应为例,当耦合系数从1逐渐减小到0.25时,其ME电压系数的数值逐渐减小为649 mV·cm-1·Oe-1,486 mV·cm-1·Oe-1,336 mV·cm-1·Oe-1和185 mV·cm-1·Oe-1;其对应的PMNT体积分数vmax则逐渐增大为0.52,0.58,0.65,0.74.造成这种情况的原因,分析认为是层间耦合状态恶化后,铁电相弹性常数和压电性能受到的影响大于铁磁相,因此需要较大的体积分数来平衡两相的差异.从计算模拟的结果来看,PMNT/NFO复合的ME电压系数的数值较大,而一般实验得到的复合薄膜的ME电压系数都较小(如PZT/LSMO复合的最大值仅为αE33≈45 mV·cm-1·Oe-1).这是因为影响薄膜复合的因素不仅包括体积比和层间耦合,还包括基片的选择,退火的温度,薄膜的取向、偏置磁场等.
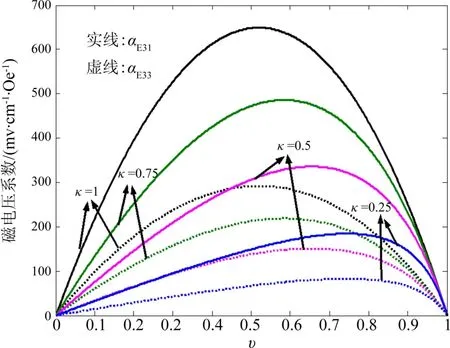
图2 磁电电压系数与铁电相体积分数v的关系Fig.2 Dependence of ME voltage coefficient on PMN-PT volume fraction v
复合磁电薄膜的磁电效应与层间耦合系数k的关系如图3所示.从图3可以看到,复合薄膜的ME电压系数与耦合系数k的关系在v=0.5,0.6,0.7时的关系近乎线性,而v=0.8时ME电压系数与耦合系数k的关系类似两条折线,在k=0.5时出现一个拐点.这可以归结为耦合系数k较小时,层间耦合较为恶化,磁电效应受两相组分比例的影响较小,因此k≤0.5时,体积分数v=0.8的ME电压系数与耦合系数k的曲线关系与其他体积分数时类似;但当耦合系数k逐渐增大,层间耦合逐渐趋于理想,两相组分的比例对磁电效应影响就变得明显了,这从v=0.7的曲线图已经有所表现,而v=0.8的组分比例近一步偏离理想的组分比例,因此就出现两条折线这样严重偏离的情况.可见,ME电压系数对层间耦合系数k和两相组分之间比例有着强烈的依赖性.
图4为三层PMNT/NFO/PMNT复合的ME电压系数αE31随铁磁相、铁电相的体积比R和k的关系曲线.从图中发现,αE31与两相体积比R的关系和αE31与PMNT体积分数v的关系比较类似(图2),均表现出随R的逐渐增大,先增大至一峰值,后逐渐减小.当R逐渐增大至10时,层间理想耦合的ME电压系数αE31从649 mV·cm-1·Oe-1下降至344 mV·cm-1·Oe-1.在层间耦合系数k逐渐变小的过程中,ME电压系数αE31也是急剧下降,其αE31峰值对应的R减小,逐渐向富铁电相偏移,这与图2的结论相同.
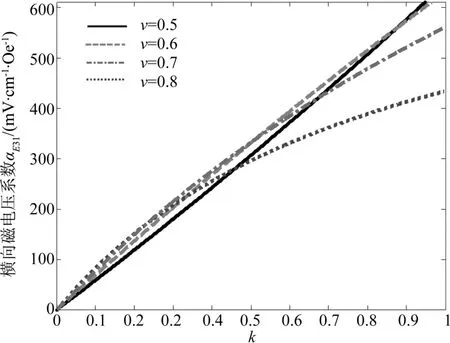
图3 横向磁电电压系数与耦合系数k的关系Fig.3 Dependence of transverse ME voltage coefficient on interface coupling k
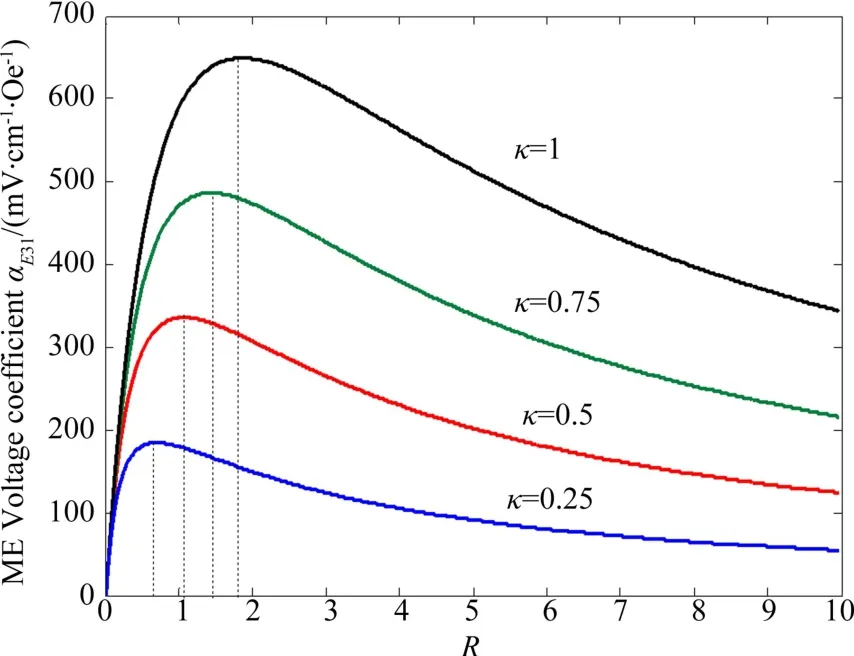
图4 三层横向ME电压系数与R的关系Fig.4 Dependence of ME voltage coefficient on R for trilayers films
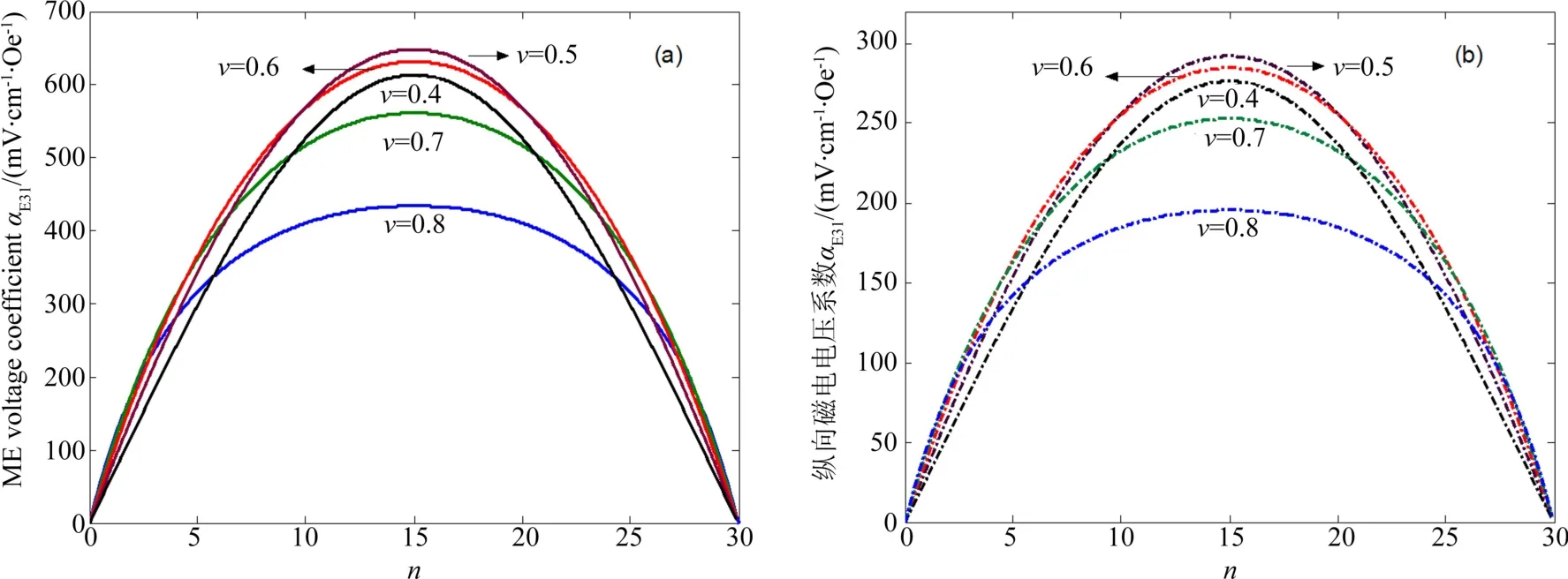
图5 磁电电压系数(a)αE31和(b)αE33与复合薄膜材料层数n的关系Fig.5 Dependence of ME voltage coefficient of(a)αE31and(b)αE33on number of composite films
图5为不同体积比的复合薄膜层数n对PMNT与NFO复合的磁电耦合效应的影响曲线.其中图5(a)与5(b)分别为横向ME电压系数αE31与纵向ME电压系数αE33与层数的关系.由图5(a)可知,对于一定的PMNT体积分数v来说,αE31与层数n的关系曲线几乎是对称的.随着层数n的增大,αE31逐渐增大,达到一最大值,之后逐渐减小,到n=30时,αE31为零.这可以解释为层数的增加导致界面的增多,界面间的应力变化间接增强了界面的耦合强度,从而导致强的磁电耦合[27-28].此外,还存在一个临界的层数n=15使得ME电压系数αE31最大,这是由于经验公式(7)在当n=15时,耦合系数k=1的缘故,可见过多的界面也会导致界面耦合的恶化.对比PMNT体积分数v=0.4,0.5,0.6,0.7,0.8的ME电压系数αE31变化曲线,发现n<10或n>20时,v=0.6对应的ME电压系数αE31值最大;当n=10~20时,v=0.5对应的ME电压系数αE31值最大.图5(b)与图5(a)得到的结论类似.由此,我们不难得出结论:选择合适的薄膜层数和两相体积比有利于设计出磁电性能更好的复合材料.
3 结论
在弹力学模型下对PMNT与NFO双层、三层以及多层复合的磁电薄膜材料的磁电效应与各参数的关系进行分析.得到以下结论:双层、三层ME电压系数具有各向异性,且随着铁电电相体积分数v先增大后减小,存在一个最佳体积比;ME电压系数随界面耦合系数呈线性急剧降低,且最佳铁电相体积分数vmax向富铁电相偏移;同时,ME电压系数与复合材料的层数n也有一定关系,在层数n=15时ME电压系数存在极大值.影响磁电效应的因素很多,如表面残余应力、晶格失配、基底等,但影响ME的主要因素还是界面耦合系数k以及两相体积比,本文的计算模拟对PMN-PT/CFO复合磁电薄膜的实验和理论工作有一定的指导意义.
[1]Eerenstein W,Mathur N D,Scott J F.Multiferroic and magnetoelectric materials[J].Nature,2006,442:759-765.
[2]Zhou Y C,Yang Z Y,Zheng X J.Residual stress in PZT thin films prepared by pulsed laser deposition[J].Surface and Coatings Technology,2003,162(2-3):202-211.
[3]Bichurin M I,Petrov V M.Theroy of low-frequency magnetoelectric effects in ferromagnetic-ferroelectric layered composites [J].J Appl Phys,2002,92(12):7681-7683.
[4]Ryu J,Carazo A V,et al.Magnetoelectric properties in piezoelectric and magnetostrictive laminate composites[J].Jpn J Appl Phys,2001,40:4948-4951.
[5]Liu Y X,Wan J G,Liu J M,et al.Numerical modeling of magnetoelectric effect in a composite structure[J].J Appl Phys,2003,94(8):5111-5117.
[6]Wan J G,Li Z Y,Wang Y,et al.Strong flexural resonant magnetoelectric effect in terfenol-D/epoxy-Pb(Zr,Ti)O3bilayer [J].Appl Phys Lett,2005,86:202504-202509.
[7]Yu H,Zeng M,Wang Y,et al.Magnetoelectric resonace-bandwith broadening of terfenol-D/epoxy-Pb(Zr,Ti)O3bilayers in parallel and series connections[J].Appl Phys Lett,2005,86:032508-032514.
[8]Nan C W,Liu L,Cai N,et al.A three-phase magnetoelectric composite of piezoelectric ceramics,rare-earth iron alloys and polymer[J].Appl Phys Lett,2002,81(20):3831-3833.
[9]Nan Cewen M I.Bichurin.Multiferroic magnetoelectric composites:Historical perspective,status,and future directions[J]. Journal of Applied Physics,2008,103(3):031101.1-031101.35.
[10]Dong S X,Zhai J Y,Li J F,et al.Magnetoelectric effect in terfenol-D/Pb(Zr,Ti)O3/μ-metal laminate composites[J]. Applied Physics Letters,2006,89(12):122903.
[11]Zhou J P,He H C,et al.Magnetoelectric CoFe2O4/Pb(Zr0.52Ti0.48)O3double-layer thin film prepared by pulsed-laser deposition[J].Applied Physics Letters,2006,88(1):013111.
[12]Zhang J X,Dai J Y,et al.Magnetoelectric coupling in CoFe2O4/SrRuO3/Pb(Zr0.52Ti0.48)O3heteroepitaxial thin film structure [J].Appl Phys Lett,2008,92(2):022901.
[13]He H C,Zhou J P,et al.Multiferroic Pb(Zr0.52Ti0.48)O3Co0.9Zn0.1Fe2O4bilayer th in films via a solution processing[J]. Appl Phys Lett,2006,89(5):052904.
[14]He H C,Wang J,et al.Ferroelectric and ferromagnetic behavior of Pb(Zr0.52Ti0.48)O3Co0.9Zn0.1Fe2O4multilayered thin films prepared via solution processing[J].Adv Funct Mater,2007,17(8):1333-1338.
[15]Zhong X L,Liao M,et al.Structural,ferroelectric,ferromagnetic,and magnetoelectric properties of the lead-free Bi3.15Nd0.85Ti3O12/CoFe2O4double-layered thin film[J].J Cryst Growth,2008,310(12):2995-2998.
[16]Guo H L,Li X D,Liu G,et al.The ferroelectric and ferromagnetic characterization of CoFe2O4/Pb(Mg1/3Nb2/3)O3-PbTiO3multilayered thin films[J].Applied Surface Science,2011,257:6573-6576.
[17]Srinivasan G,Rasmussen E T,Hayes R.Magnetoelectric effects in ferrite-lead zirconate titanate layered composites:The influence of zinc substitution in ferrites[J].Phys Rev B,2003,67:014418.
[18]Nan C W.Magnetoelectric effect in composites of piezoelectric and piezomagnetic phase[J].Phys Rev B,1994,50:6082.
[19]Dong S X,Li J F,Viehland D.Longitudinal and transverse magnetoelectric voltage coefficients of magnetostrictive/piezoelectric laminate composite:Theory[J].IEEE Trans Ultrason Ferroelectr Freq Control,2003,50:1253.
[20]Wang L,Yang C T,Xie Q T,et al.The modeling and analysis of magnetoelectric effect in bilayer nanocomposites[J].Acta Phys Sin,2009,5:3515-3519.
[21]Bichurin M I,Petrov V M,Srinivasan G.Modeling of magnetoelectric effect in ferromagnetic/piezoelectric multilayer composites[J].Ferroelectrics,2002,280:165-175.
[22]Srinivasan G,Hayes R,Devreugd C P,Laletsin V M,Paddubnaya N.Dynamic magnetoelectric effects in bulk and layered composites of cobalt zinc ferrite and lead zirconate titanate[J].Appl Phys A,2005,80:891-897.
[23]Cao H,Fang B J,et al.Elastic,dielectric,piezoelectric and electronmechanical propeties of tetragonal Pb(Mg1/3Nb2/3)O3-PbTiO3(PMN-PT)[J].J Inorg Mater,2003,18(2):465-469.
[24]Wu J G,Wang John.Multiferroic behavior and impedance spectroscopy of bilayered BiFeO3/CoFe2O4thin films[J].J Appl Phys,2009,105:124107.
[25]Bichurin M I,Filippov D A,Petrov V M.Resonance magnetoelectric effects in layered magnetostrictive-piezoelectric composites[J].Phys Rev B,2003,68:132408.
[26]Wang Y,Ma Y,Xu X,et al.Antiferromagnetic magnetization and exchange anisotropy in ferromagnetic/antiferromagnetic/ferromagnetic trilayers[J].Chinese J Comput Phys,2010,27(1):137-142.
[27]Zhang J X,Dai J Y,Chan H L W.Interfacial engineering and coupling of electric and magnetic properties in Pb(Zr0.53Ti0.47)O3/CoFe2O4multiferroic epitaxial multilayers[J].J Appl Phys,2010,107:104105.
[28]Liu Y,Zhang Y,Lin Y H,et al.Magnetoelectric coupling in BaTiO3/(NiFe2O4/BaTiO3)n(n=1,2,3,4)multilayered thin films[J].J Appl Phys,2009,105:083915.
Simulation on 2-2 Type PMNT/NFO Composite Magnetoelectric Effect
YANG Huanyin,FAN Dongmei,GUO Hongli
(Institute of Condensed Matter Physics,Yangtze Normal University,Chongqing 408100,China)
In an elastic mechanics model,a magnetoelectric composites constitutive equation was established.Longitudinal and transverse ME voltage coefficient formulas of double-layer and three-layer composited thin films of 2-2 type in non-ideal condition were deduced with ferroelectric and magnetic constitutive equation.Composite ME voltage coefficient of ferromagnetic phase material nickel ferrite(NFO)and ferroelectric phase material lead magnesium niobate-lead titanate(PMNT)are studied.Relations between ME voltage coefficient and PMNT volume fraction,interface coupling parameters,two phase volume ratio and total number of layers are analyzed.It shows that performance of two phase material,appropriate volume fraction,coupling coefficient and total layer number are key to ME voltage coefficient.
magnetoelectric effect;couple;composite material;constitutive equations
date:2013-09-15;Revised date:2014-02-28
O482.5
A
2013-09-15;
2014-02-28
重庆市教委项目基金(KJ121317)和长江师范学院科技项目基金(2012XJYB065)资助
杨焕银(1983-),女,工学硕士,山东肥城,研究方向:计算物理及低维纳米制备,E-mail:yuxinyin83@163.com
*通讯作者:郭红力(1981-),男,工学博士,副教授,研究方向:功能性铁电及多铁复合薄膜
1001-246X(2014)05-0587-06

