产水气井井筒温度压力计算方法
李 波, 甯 波, 苏海洋, 刘 虹, 位云生
(中国石油勘探开发研究院,北京 100083)
产水气井井筒温度压力计算方法
李 波, 甯 波, 苏海洋, 刘 虹, 位云生
(中国石油勘探开发研究院,北京 100083)
应用考虑气液相间滑脱与流体沿井筒截面非均匀分布的漂移模型,结合动量守恒、能量守恒和井筒传热学,建立考虑井斜变化的气井井筒温度、压力耦合预测模型,通过15口实测井数据对模型进行验证.结果表明:所建模型可以准确计算产水气井井筒的温度和压力,计算结果平均绝对误差3.60%,满足工程计算要求.
多相流;漂移模型;温度;压力;致密砂岩气井
0 引言
地层流体(油、气、水)从井底向井口流动过程中往往伴随着许多复杂的物理现象,流动型态一般包括泡状流、段塞流、过渡流和环雾流[1-7].井筒多相流动常用的处理方法有三种:经验模型,均质模型和机理模型.经验模型根据多相流体运动的物理概念和物性参数,利用因次分析法或根据基本运动方程得到描述某种特殊流动的无因次参数建立多相流动的经验关系式.截止目前,国内外已有许多经验模型[1-7],但在实际运用中,经验模型需要大量的计算过程来判断流型.此外,在某些流型之间的过渡区可能出现压降和持液率的不连续现象,这样就使得在求解井筒压力和持液率等参数时出现不收敛或不连续.均质模型采用单相流的处理方法,认为气体和液体的流速相等,但这与实际情况不符,特别是在气体流动含量较低、流动速度较慢的情况下[8-10].机理模型通常被认为是最精确的模型,因为它是在详细描述不同流型的物理现象的基础上提出的,但是其方程系统复杂,求解困难,以及在某些流型的过渡区可能出现压降和持液率不连续从而使计算不收敛,因此没有被广泛运用.
由于漂移模型具有相对简单、连续可微的优点,适用于井筒多相流动建模.为此,对漂移模型开展了大量的研究[8-16],本文对漂移模型的重要参数(分布系数和漂移速度)进行比较优选,建立适合井筒多相流动的漂移模型.通过漂移模型计算井筒任意深度的截面含气率及流体物性参数,再根据井筒传热学、动量守恒和能量守恒,建立井筒温度和压力耦合模型,通过分段迭代法对模型进行求解,并运用15口产水气井实测数据对模型进行验证,计算一口实例水平井井筒压力、温度分布.
1 漂移模型
在井筒气液两相流动过程中,由于气相和液相的密度不一样,存在气相超越液相流动的现象,即气液两相间存在滑脱,因此采用简单的均相模型来计算井筒的温度和压力分布会有一定的偏差.1965年,Zuber&Findlay[8]首次提出考虑了气液相间的滑脱现象,以及气相沿井筒径向的变密度分布的漂移模型.而后,Bankoff[9],Wallis[10],Ishii[15-16],Hasan&Kabir[19-20],Ansari[5]等对漂移模型进行了改进,使其广泛用于核工业和石油工业中的多相流动建模.由于漂移模型具有连续、可微和相对简单的特点,Holmes等[13]于1997年将漂移模型引入数值模拟复杂结构井井筒等温多相流动建模,但是由于之前的模型参数大多适合小直径管流,不能直接用于井筒或地面设备中的多相流动建模[14-15].为此,Oddie&Shi等[14-16]开展了大量的实验,对模型参数进行了回归分析,并建立了适合大尺寸井筒多相流动的漂移模型.本研究的目的是通过研究前人所建立的漂移模型,建立适合大尺寸井筒非等温多相流动的漂移模型,为准确计算井筒温度和压力分布提供前提.
1.1 漂移模型的基本关系式
气液两相流动情况下,气相与液相间的滑脱现象是由于以下两种机理结合产生的.一是气体管横截面上速度剖面和相分布剖面不一致,气相在管中央处分布最高,管中央处混合物的流动速度也最快,如图1所示.因此,整个截面上气相的平均速度要比液相的平均速度大.另外一种机理就是气体受浮力的作用,倾向于垂直向上运动.
考虑以上两种机理的模型,气体的截面平均流速可表示为

式中,vg为气体的截面平均速度,m·s-1;Co为分布系数(描述两相的分布特性,即流动型态特性),无因次;vm为混合物的截面平均流速(无滑脱),m·s-1;vd为气体的漂移速度(描述浮力效应),m·s-1.
混合物的截面平均速度是气相和液相折算速度之和,即
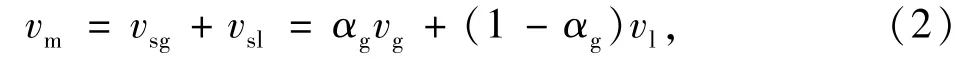
式中,vsg为气体折算速度,m·s-1;vsl为液体折算速度,m·s-1;αg为截面平均含气率;vl为液相的流动速度,m·s-1.
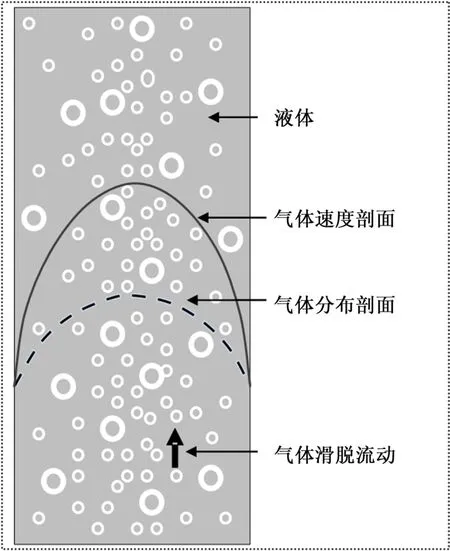
图1 漂移模型示意图Fig.1 Drift-flux model
1.2 漂移模型的关键参数
1.2.1 分布系数Co
Zuber&Findlay给出Co的取值范围是1~1.5[8].对于泡流和段塞流,Aziz、Ansari和Hasan&Kabir给出Co取值为1.2;而对于环雾流,Co取值接近于1.0[4-5].此外,在αg为1.0(高气液比)时,Co的值也应为1.0.与此同时,αgCo的值不能超过1.0.因此,Co表达式必须使其值在泡流和段塞流情况下有恒定不变的值,并且在αg为1.0时或混合物速度增大时,Co取值减小为1.0,即

为了使Co在αg和vm较大时取值减小到1.0,γ采用如下表达式
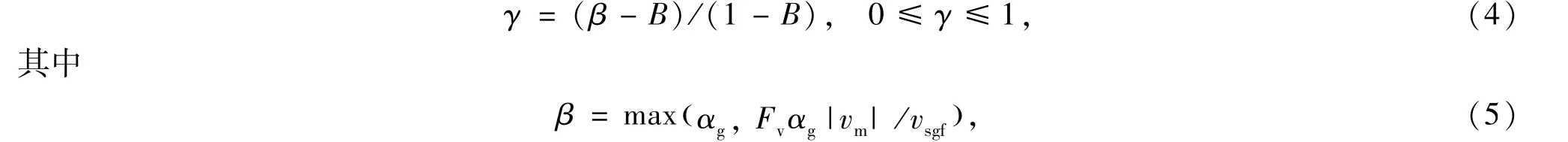
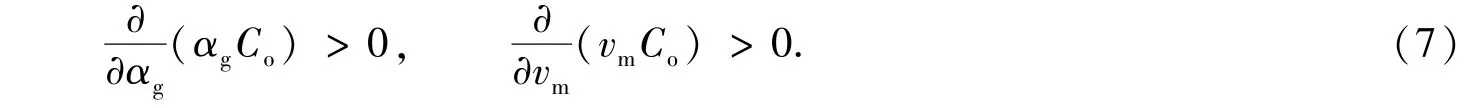
在以上条件不能满足时,可能会出现不稳定的情况.在B<(2-A)/A时,以上两个条件都成立.
1.2.2 漂移速度vd
漂移速度是气液混合物流动过程中气液相对运动的截面平均速度值.在截面含气率αg较小时,气体漂
式中,vsgf为淹没速度,即气相折算流速到达足以使沿管壁液膜不会掉落下来时的速度值,流体的流动将出现环状流.参数A,B和Fv需要通过实验进行调整,根据Oddie&Shi等[14-16]人的实验及模型参数优化结果,气液两相流情况下,A取1.2,B取0.3,Fv取1.0.
淹没速度用Wallis等[3]给出的关系式进行求解

式中,ku是临界Kutateladze数,具体算法请参考文献[15];vc为特征流速,由式(8)进行计算.
显然,气相折算速度(vsg=αgvm)随αg和vm的增加而增加.因此,Co必须满足以下关系式移速度与气体从静止液体中向上移动速度有关,Harmathy[11]得到其值为1.53 vc,vc表达式为

式中,σgl为气-液相的表面张力,N·m-1;g为重力加速度,m·s-2;ρl为液相密度,kg·m-3;ρg为气相密度,kg·m-3.
在αg取较大值时,可能出现气液相沿不同方向流动的逆流情况[14].在逆流的限制条件(vsg>0,vsl<0)的情况下,漂移速度是αg的函数,即有
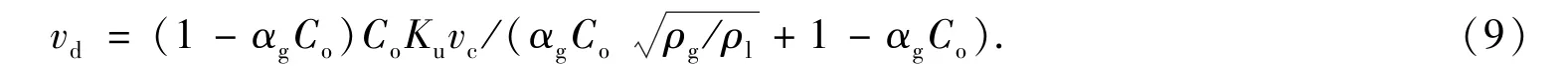
对于处在以上两种极端情况之间的过渡区,则通过选用两个临界的截面含气率a1和a2,然后插值进行确定漂移速度.根据Oddie&Shi等[14-16]人的实验结果,a1取0.06,a2取0.21.
综合考虑以上情况,漂移速度的总表达式为
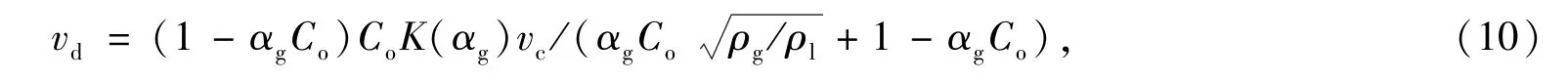
式中,当αg≤a1时,K(αg)=1.53/Co;当αg≥a2时,K(αg)=Ku();在a1<αg<a2时,通过线性插值得到其值.
对于倾斜管流,鉴于Beggs&Brill对倾斜管流的处理方法,基于垂直管中的流动情况,Hasan&Kabir[4]提出采用下式进行修正

其中,θ为倾斜角,(°);m(θ)为倾斜影响因子;vdθ是倾角为θ时的漂移速度,m·s-1;vd0为垂直流下的漂移速度,m·s-1.
对于气液两相流动系统,Hasan-Kabir[4]提出m(θ)采用下面式子进行计算

根据Oddie&Shi等[14]在大管径倾斜管流实验,倾斜影响因子采用下式计算结果与实验结果吻合更好
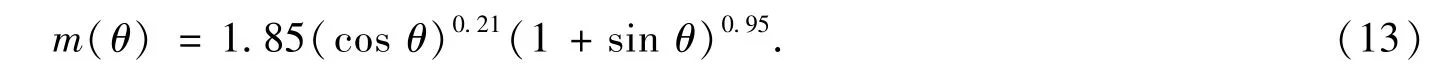
由以上研究可知,通过确定出漂移模型的两个重要参数(分布系数和漂移速度),便可以得到井筒的截面处含气率,进而确定该井筒处流体的平均物性参数.但从式(4)、(3)、(10)可知:分布系数、漂移速度和截面含气率之间互为隐函数,因此需要进行迭代求解.
2 井筒温度压力计算模型
地层流体从井底流向井口过程中,不断向地层中散发热量,以及需要克服重力和摩擦力作用,井筒温度、
压力不断降低,而流体物性又与温度、压力之间相互影响,因此需要建立温度、压力和物性耦合模型,采用迭代法进行求解.
2.1 井筒压力计算模型
油气井井筒压力分布计算是油气井生产设计、动态分析和预测的核心问题.在此,假设流体在井筒中的流动为一维稳定流动,从管流系统任取一控制单元,建立如图2所示的坐标系.由动量守恒定理有
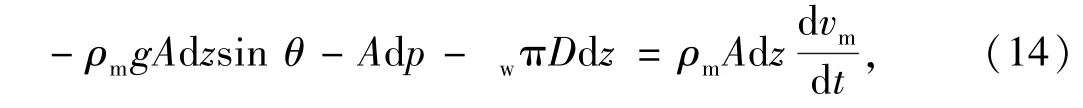
式中,ρm为混合物密度,kg·m-3;A为井筒截面,m2;D为井筒直径,m;θ为井筒倾斜角,(°);vm为混合物流速,m·s-1;w为管壁摩擦力,N;dp为压力变化量,Pa;dz为井筒长度,m.
整理得到压力梯度
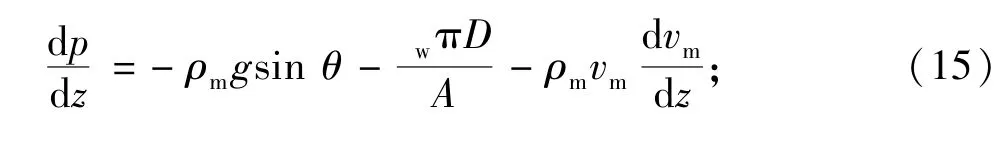
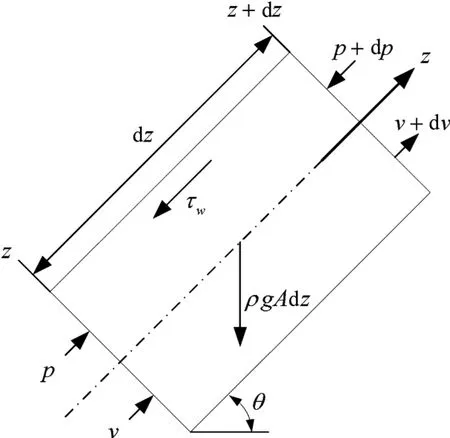
图2 井筒一维流动示意图Fig.2 One-dimensional flow in wellbores
通过引入摩擦阻力系数fm,压力梯度方程可表示为
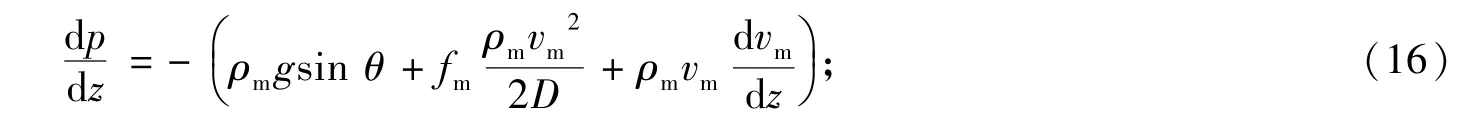

式中,ε为管壁粗糙度,mm;D为管径,mm;Λ为无因次参数,Λ=(ε/D)1.109 8/2.825 7+(7.149/Rem)0.898 1;Rem为无因次雷诺数,Rem=Dυmρm/μm.
混合物的密度ρm和混合物的粘度μm分别采用体积加权和质量加权:

式中φ为截面体积含气率(通过漂移模型计算),小数;x为截面质量含气率,小数;μg、μl为气体、液体粘度,mPa·s.
2.2 井筒温度计算模型
地层中的流体通过井筒从井底流到井口的过程中,地层温度与井筒内流体之间存在温度差,井筒中流体与地层之间存在热量交换,此外,流体自身的各种能量也会相互转化.根据Ramey、Willhite、Hasan&Kabir、毛伟和廖新维等[17-23]人研究,井筒传热可作以下简化假设:①流体在井筒中的流动为一维稳定流动;②气液间不存在质量交换;③井筒与地层之间只进行热量径向传递,热量径向传递包括两个过程:井筒到水泥外沿之间的稳态传热,以及水泥环外向地层深处的非稳态传热.
由能量守恒定律有

摩擦阻力系数fm可以采用Chen方法进行计算,
式中,h为流体的比焓,J;q为流体的径向热容量,J·s-1.
由热力学第一定律,得到流体比焓梯度

式中,cP为流体的定压比热容,J·(kg·℃)-1;Tf为油管内流体流动温度,℃;αJ为焦耳—汤姆逊系数,℃·Pa-1.
在单位长度井段上,流体从油管到井壁的热流量梯度为

式中,Tf为井筒流体温度,℃;Th为井壁温度,℃;Uto为总传热系数,W·(m·℃)-1;Wm为质量流量,kg·s-1.
根据Hasan&Kabir[17]提出的无因次时间函数f(tD),引入松弛因子A,由式(20)~(22)可得到井筒温度梯度方程为
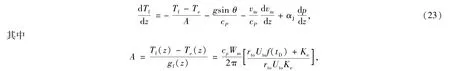
式中,Te是地层温度,℃;ke是地层导热系数,W·(m·℃)-1;rto是套管外径,m.考虑焦耳—汤姆逊效应,稳定流动情况下(23)式的解析解为
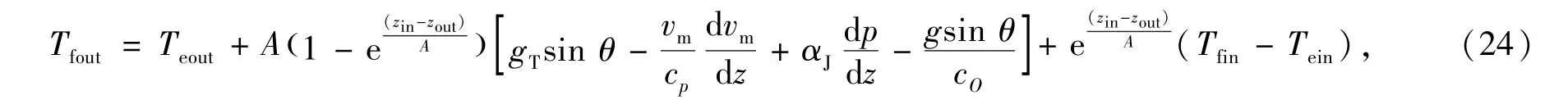
式中,Teout、Tein是计算段的出口和入口地层温度,℃;zout、zin为计算段出口和入口深度,m;gT为计算井段处的地温梯度,℃·m-1.
2.3 井筒温度、压力计算
由于井筒中流体物性、温度和压力之间关系紧密,相互影响,因此在计算井筒温度和压力时,需要进行耦合迭代求解.迭代求解面临一个重要的问题是如何给定初值,因为初始值会影响迭代的收敛速度,本文采用(25)式计算井筒流出初始温度值.
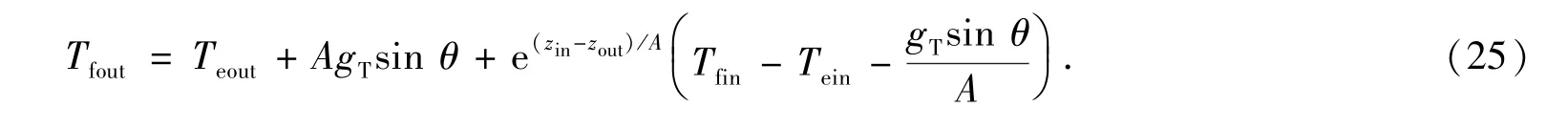
温度、压力耦合迭代计算详细步骤如下:
1)给定井底条件:Tfin=TeBH,Tein=TeBH,pin=pBH,并选取合适的ΔL将井筒分为n段.
2)根据(25)式计算粗略出口温度Tfout.
3)估计ΔL段压力变化量Δp估计,利用漂移模型计算各相流体的流动速度和持率.
5)根据(16)式计算ΔL段压降梯度,然后计算出ΔL段的压力变化量Δp计算.
6)比较压力变化估计量Δp估计和计算值Δp计算,若二者之差不满足条件,则将值Δp计算作为初值,重复3)~6)步,直到满足条件为止.
7)计算井筒总传热系数和焦耳—汤姆逊系数,利用(24)式精确计算段出口段的温度值.
8)比较第3)步与第7)步的温度变化值,若二者之差满足要求,则进行下一段温度压力计算;否则,将第7)步计算的温度变化值作为温度初始值,跳到第2)步进行,重新计算,直到满足要求为止.
9)计算该计算段对应的深度Li、压力pi和出口温度Ti
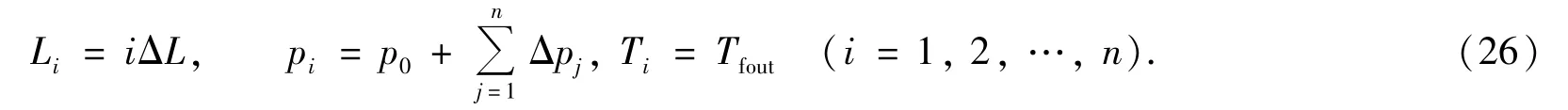
10)将Li处的压力pi和Tf作为下一计算段的入口参数,重复2)~9)步计算下一深度Li+1的压力pi+1和温度Ti+1,直到算完整个井筒温度和压力.
3 模型验证与实例计算
3.1 模型验证
A气田为典型致密砂岩气藏,气藏平均压力系数为0.87,温度110℃,天然气相对密度0.598.气藏油水关系复杂,气井普遍产水,产出水包括凝析水和层间水.取A气田15口典型气井测试资料对所建模型进行评价,气井产气量为(3.98~14.59)×104m3·d-1,产水量为(1.11~18.34)m3·d-1,平均气水比1.14× 104m3·m-3,井底流压(21.54~28.62)MPa,测试井口压(21.54~28.62)MPa,测试井口压力(11.43~22.43)MPa,井的基本参数与实测如表1所示.油管直径62 mm,管壁相对粗糙度0.004 5.
由模型计算井口压力与实测井口压力对比可知(表2、表3、图3),模型计算井口压力与实测压力误差均小于10%,平均误差-0.38%,平均误差标准偏差为4.21%,平均绝对误差为3.60%,平均绝对误差标准差为2.22%,是参与评价模型中误差最小的,其次是Hagedorn-Brown计算结果较好.而在油井管流计算中常用的Beggs-Brill和Orkiszewsiki模型,计算结果误差较大,原因是这两种模型都是通过实验建立的经验关系式来计算井筒截面处的流体物性,受实验参数范围(如:流量、气液比等)和实验条件(如:管径、管长等)的限制,这些经验关系式对低流速、较低气液比的油井多相流计算具有较高精度,而对高流量、高气液比气井则适应性较差,计算结果误差较大.
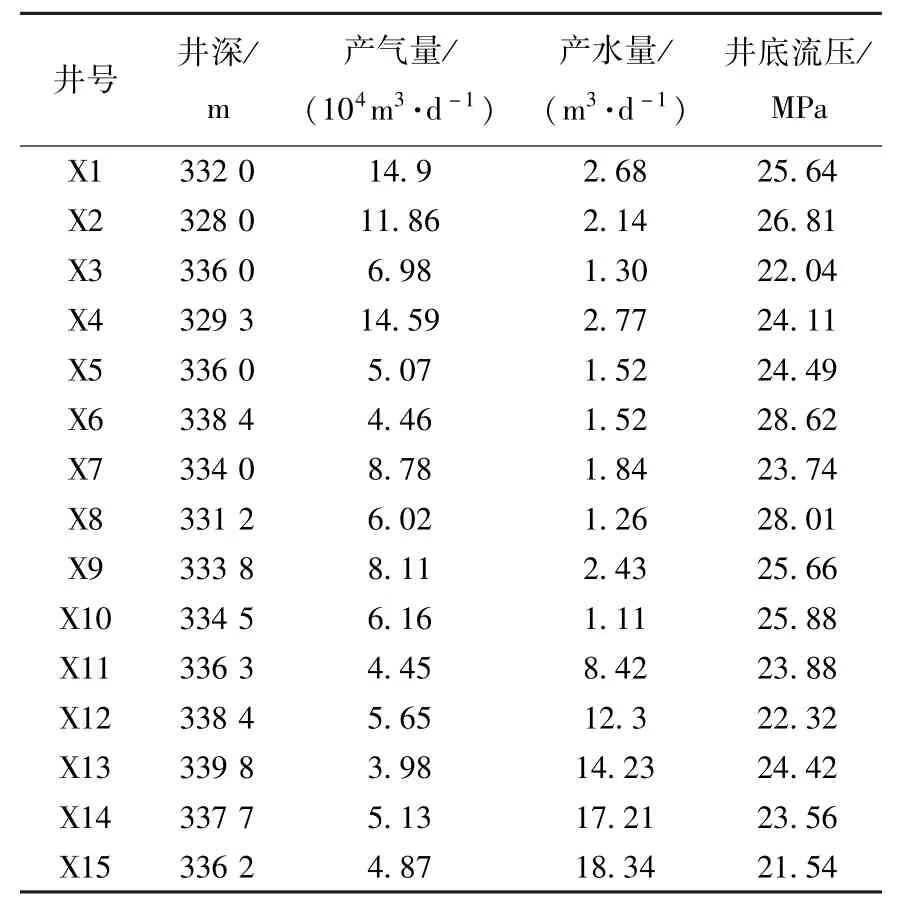
表1 气井基本参数表Table 1 Basic data of gas wells
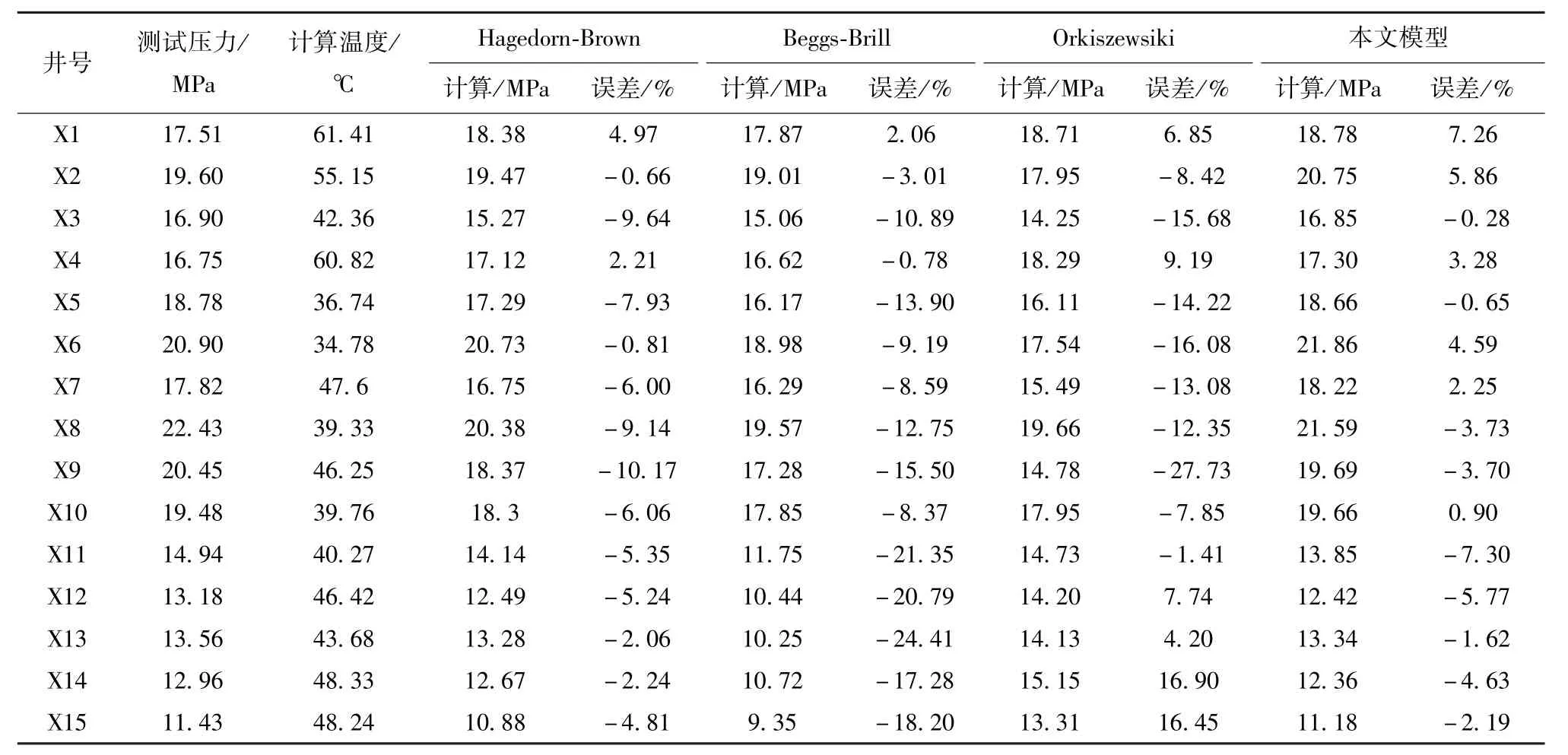
表2 模型计算井口压力与实测井口压力对比Table 2 Comparison between calculated wellhead pressures and measured wellhead pressures
通过所建模型计算还得到了井口温度,但由于缺少现场井口温度测试数据,不能进行温度误差分析.根据文献[21]的观点,如果温度和压力是通过耦合计算得到的,只要压力计算结果准确,可以认为温度计算结果也可靠.此外,利用本文所建模型对文献[23]中的实例气井进行计算,计算温度、压力值与实测温度、压力值误差分别为1.54%和2.34%,说明本文计算方法是准确的.因此,可以认为本文建立的温度压力预测模型可靠,满足工程计算要求.
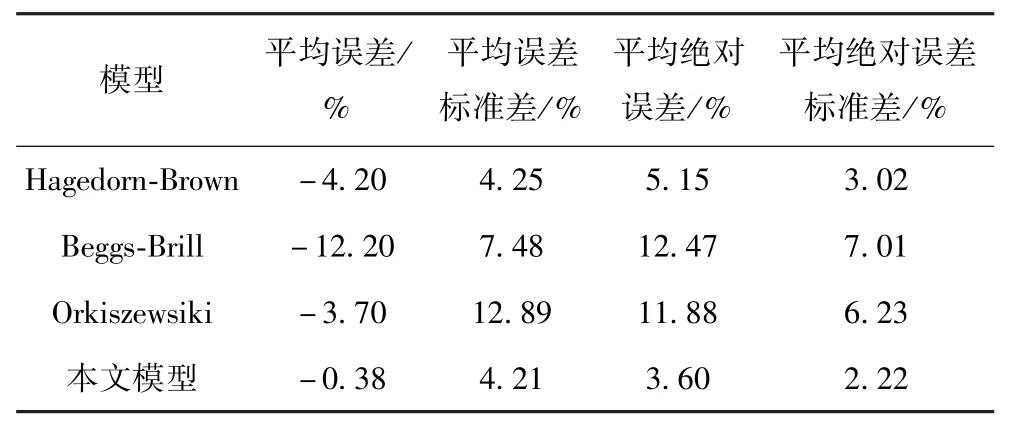
表3 计算结果误差分析Table 3 Error analysis of results
3.2 实例井计算
长深D平6井位于长岭断陷中部隆起带哈尔金构造上,完钻井深4 207 m,水平段长1 007 m,水平段中深3 864 m,采用水平段裸眼封隔器+滑套完井.为满足产气与临界携液要求,采用73 mm油管进行生产.该井压裂投产后日产气19.53×104m3,水气比1.77 m3·(104m3)-1,天然气相对密度为0.59,井底流压33.50 MPa,井底温度133℃.
由井筒温度与压力分布计算结果(图4)可知,地层流体从井底向地面流动过程中,由于克服重力、摩擦力和速度变化,井筒压力不断降低;井筒温度不断降低,但始终大于地层温度,并且差值越来越大,这主要是由于流体从地层深部携带的热量由于温差需要不断向地层中散发热量造成的.通过计算:流体达到井口后温度为65.68℃,油压为20.61 MPa,计算油压与井口实测油压20.42 MPa,误差仅为1.89%,模型计算精度较高.此外,在水平井的水平段中点至造斜段(3 120 m~3 864 m),井筒和温度下降较慢;从井底到井口的总压降为12.892 0 MPa,其中加速度压降为0.001 9 MPa,摩擦压降3.801 3 MPa,重力压降9.088 8 MPa,可以看出井筒中的压降主要是由摩擦力和重力引起的,而加速压降则相对较小.
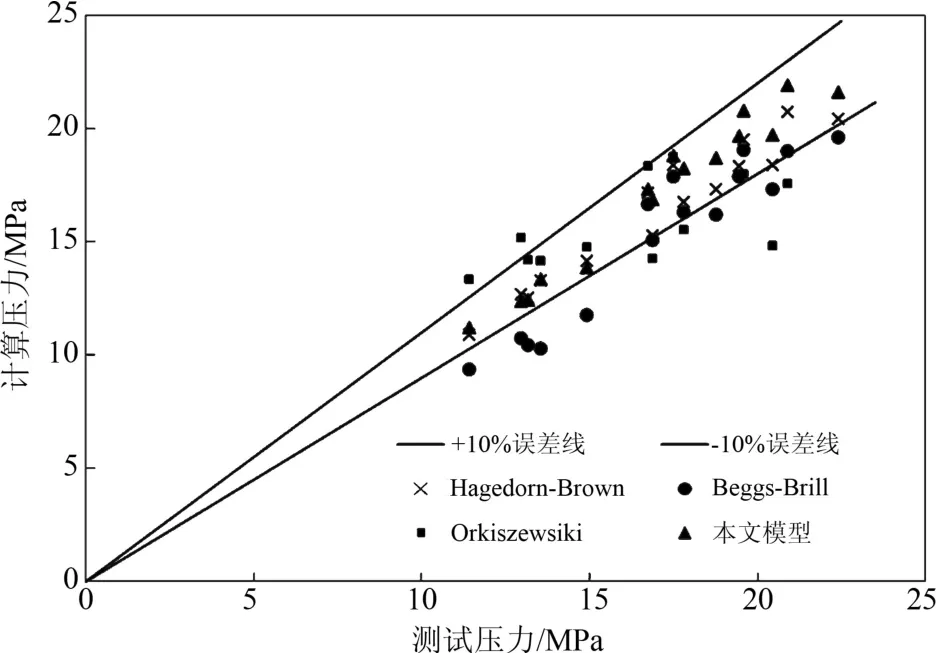
图3 模型计算压力与实测井口压力对比Fig.3 Comparison of calculated wellhead pressure with measured values
4 结论
1)漂移模型考虑了气液相间的滑脱和流体沿井筒截面的非均匀分布,且具有相对简单、连续可微的特点,可以准确计算任意倾角情况下井筒截面处的流体分布,适合用于井筒多相流动建模.
2)基于漂移模型的井筒温度、压力耦合预测模型可以计算产水气井井筒的温度和压力分布,以及流体的物性参数,计算过程相对简单.对高气液比产水气井,所建模型计算精度高于常用的Hagedorn-Brown、Beggs-Brill和Orkiszewsiki模型,平均绝对误差仅为3.60%,满足工程计算要求.
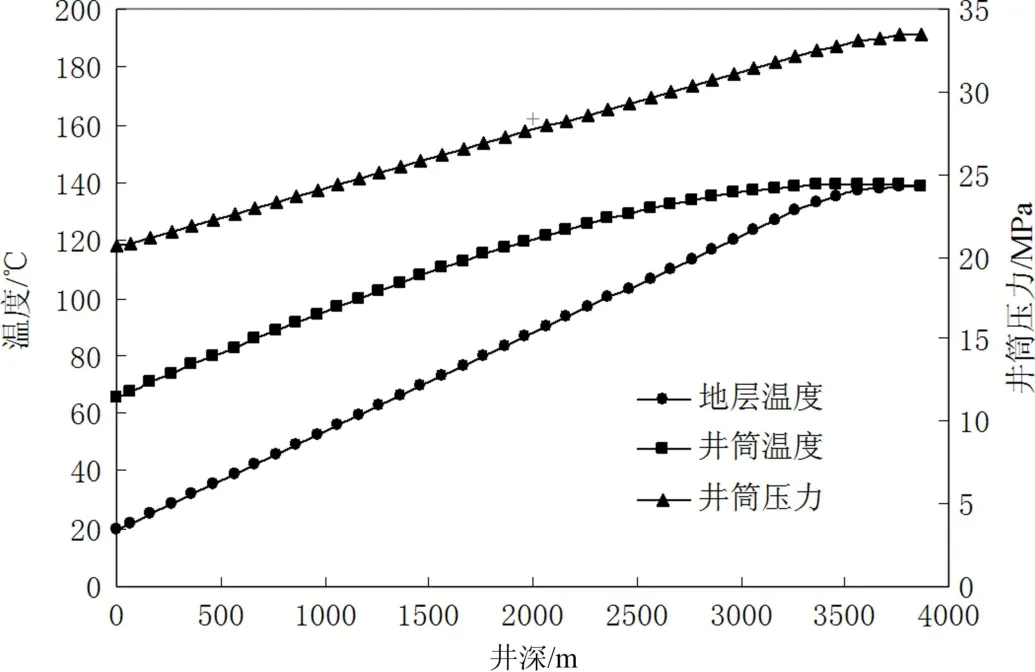
图4 井筒温度和压力分布Fig.4 Temperature and pressure distribution in wellbores
[1]Hagedorn A R,Brown K E.Experimental study of pressure gradients occurring during continuous two-phase flow in small diameter vertical conduits[J].JPT,1965,(4):475-484.
[2]Orkiszewski J.Predicting two-phase pressure drops in vertical pipes[J].JPT,1967,23(6):829-838.
[3]Beggs H D,Brill J P.A study of tow-phase flow in inclined pipes[J].JPT,1973,25(5):607-617.
[4]Hasan A R,Kabir C S.Predicting multiphase flow behavior in a deviated well[J].SPE Prod Eng,1988,474(11):475-482.
[5]Ansari A M,Sylvester N D,Sarica,et al.A comprehensive mechanistic model for upward two-phase flow in wellbores[J]. SPE Prod&Faci,1994,9(2):143-151.
[6]Gomez L E,Ovadia S,Zelimir S,et al.Unified mechanistic model for steady-state two-phase flow:Horizontal to vertical upward flow[J].SPE Journal,2000,5(3):339-350.
[7]Kaya A S,Sarica C,Bill J P.Mechanistic modeling of two phase flow in deviated wells[J].SPE Prod&Faci,2001,(9):156-166.
[8]Zuber N,Findlay J.Average volumetric concentration in two-phase flow systems[J].Heat Transfer Trans ASME,1965,87:453-468.
[9]Bankoff S G.A variable density,single fluid model for two-phase flow with particular reference to steam-water flow[J].Heat Transfer Trans ASME,1960,82:265-272.
[10]Wallis G B,Makkenchery S.The hanging film phenomenon in vertical annular two-phase flow[J].Trans ASME,1974:186-197.
[11]Harmathy T Z.Velocity of large drops and bubbles in media of infinite and restricted extent[J].AIChE J,1960,6(2):281-288.
[12]Hibiki T,Ishii M.One-dimensional drift-flux model for two-phase flow in a large diameter pipe[J].International Journal of Heat and Mass Transfer,2003,46:1773-1790.
[13]Holmes J A,Barkve T,Lund O.Application of a multi-segment well model to simulate flow in advanced wells[R].SPE 50646,1998.
[14]Oddie G,Shi H,Durlofsky,et al.Experimental study of two and three phase flows in large diameter inclined pipes[J]. Multiphase Flow,2003,29:527-558.
[15]Shi H,Holmes J A,Durlofsky,et al.Drift-flux modeling of two-phase flow in wellbores[J].SPEJ,2005,10(1):24-33. [16]Shi H,Holmes J A,Diaz L R,et al.Drift-flux parameters for three-phase steady-state flow in wellbores[J].SPEJ,2005,10 (2):130-137.
[17]Ramey H J.Wellbore heat transmission[J].Trans,AIME,1962,14(4):427-435.
[18]Willhite G P.Over-all heat transfer coefficients in stream and hot water injection wells[J].JPT,1967:607-615.
[19]Hasan A R,Kabir C S.Aspects of heat transfer during two-phase flow in wellbores[J].SPE Prod&Faci,1994,9(3):211 -216.
[20]Hasan A R,Kabir C S,Wang X.A robust steady-state model for flowing-fluid temperature model in complex wells[J].SPE Prod&Oper,2009,24(2),269-276.
[21]Mao Wei,Liang Zheng.New method of calculating wellbore temperature in gas wells[J].Journal of Southwest Petroleum Institute,1999,21(1):56-66.
[22]Mao Wei,Liang Zheng.Coupling analysis of the pressure and temperature in gas well borehole[J].Natural Gas Industry,1999,19(6):66-68.
[23]Liao Xinwei,Feng Jilei.Pressure-temperature coupling calculation of transient wellbore heat transfer in deep geopressured gas reservoir[J].Petroleum Exploration and Development,2005,32(1):67-69.
[24]Wu Xiaodong,Wu Han,Han Guoqing,et al.A new model for calculating wellbore temperature and pressure distribution of a high-H2S gas well considering the influence of the sulfur release in wellbores[J].Natural Gas Industry,2011,31(9):69-72.
A Calculation Method for Temperature and Pressure Distribution in Water Production Gas Wellbores
LI Bo,NING Bo,SU Haiyang,LIU Hong,WEI Yunsheng
(Research Institute of Petroleum Exploration&Development,Beijing 100083,China)
Based on drift model which copes with gas-liquid phase slippage and non-uniform distribution along section of wellbore,a coupled temperature-pressure prediction model was established for varied angle gas wellbores considering momentum conservation,conservation of energy and wellbore heat transmission.The model was validated with 15 tested gas wells.The calculation showed satisfying results with average absolute error of 3.6%which meets engineering requirements.
multi-phase flow;drift model;temperature;pressure;tight sandstone gas wells
date:2013-08-21;Revised date:2014-03-04
TE319
A
2013-08-21;
2014-03-04
国家科技重大专项(2011ZX05015)资助项目
李波(1985-),男,贵州思南,博士生,从事气藏工程与多相管流研究,E-mail:libosonova@163.com
1001-246X(2014)05-0573-08

