基于有限元法的耦合微带线分布电容参数的计算

杨莉，逯贵祯

(中国传媒大学信息工程学院，北京 100024)



基于有限元法的耦合微带线分布电容参数的计算

杨莉，逯贵祯

(中国传媒大学信息工程学院，北京 100024)

耦合微带线之间的串扰问题与其分布参数密切相关。本文采用有限元方法分别对接地平面之间的对称耦合微带线、均匀介质中的两条不对称耦合微带线以及位于介质层中的三条耦合微带线等耦合微带线结构进行建模，得到了三种结构的电势分布图，并计算了这三种结构的单位长度分布电容矩阵。与文献中结果对比，计算结果一致性很好，方法可行有效。

耦合微带线；电容矩阵；有限元法；电磁兼容

1　引言

传输线之间的串扰分析是信号完整性分析中经常遇到的问题。耦合微带线是典型的传输线结构，其串扰问题与微带线之间的单位长度分布电容、分布电感等电参数密切相关。研究和分析耦合微带线之间的分布参数对于设计和优化高速数据信号的传输具有重要的工程应用意义。

目前计算耦合微带线单位长度分布电容参数的方法主要有：有限元法[1-3]、矩量法[4，5]、谱域法[6]以及域分解法[7]等等。这些方法中，有限元法具有模拟各种不规则形状导线的优点，也更适用于非均匀复杂介质。

本文采用基于标势的麦克斯韦静电场有限元方法，运用静电二维环境，分别对接地平面之间的对称耦合微带线、均匀介质中的两条不对称耦合微带线以及位于介质层中的三条耦合微带线等三种耦合微带线结构进行建模，计算得到了耦合微带线模型的二维表面电势分布图，同时从电容定义出发，计算了这三种耦合微带线模型的单位长度分布电容矩阵，并将数值结果与文献中得到的结果进行对比，可以看出计算结果一致性很好，方法可行有效。

2　理论分析

对于理想导体的耦合微带传输线，电磁波沿导线传播TEM平面波。运用静电场二维有限元方法对耦合微带线进行分析计算时，定义静电标势Φ，则

E=-▽Φ

(1)

将式(1)代入麦克斯韦静电场方程，则

(2)

建立关于标势Φ的有限元变分方程

δF(Φ)=0

(3)

其中

(4)

由电容定义可知，耦合微带传输线单位长度的电容C与单位长度的电荷Q和电势V有关，其关系为：

Q=C·V

(5)

式(5)用矩阵表示为

(6)

式(6)也可表示为

(7)

3　建模与数值计算

这里，利用有限元方法对三种耦合微带线模型的单位长度分布电容矩阵进行计算和讨论。其中模型1为位于自由空间中的两接地平面之间的对称耦合微带线结构，模型2为放置在均匀媒质中的两接地平面之间的两条不对称耦合微带线结构，模型3为放置在非均匀媒质中的三条耦合微带线结构。

为了方便与文献中结论进行比较，运用二维静电环境对三种模型进行建模计算。在模型的边界条件设置时，设置接地平面的电势V=0，微带线端口则根据需要可设置成V=0或者V=1。

3.1接地平面之间的对称耦合微带线

图1所示为位于两个接地平面之间的对称耦合微带线的横截面结构示意图。该耦合微带线放置在自由空间中，其参数为：两条微带线厚度为1mm，宽度为3mm，微带线之间的间隔距离为2mm，微带线与底层地平面之间的距离为1mm，两个地平面之间的距离为5mm。将左侧微带线作为端口1，右侧为端口2，将端口1作为输入端口，设置该端口电势V=1。利用有限元方法对该结构进行建模计算，可得到该结构的二维表面电势分布图，如图2所示，然后利用式(5)，计算得到该结构的单位长度分布电容矩阵。表1中列出了该结构单位长度分布电容的计算结果，并和文献中的结果进行了比较，可以看出，结果一致性很好。

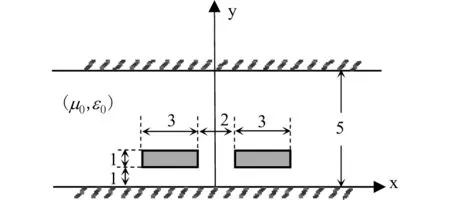
图1　两个接地平面之间的对称耦合微带线横截面结构

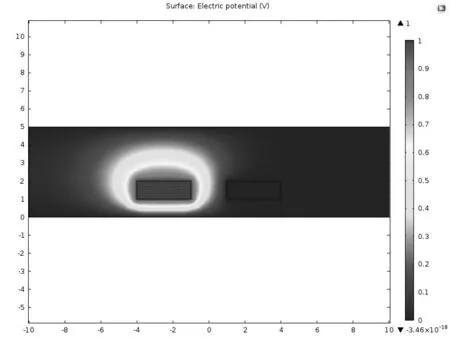
图2　端口1电势V=1时对称耦合微带线的二维表面电势分布

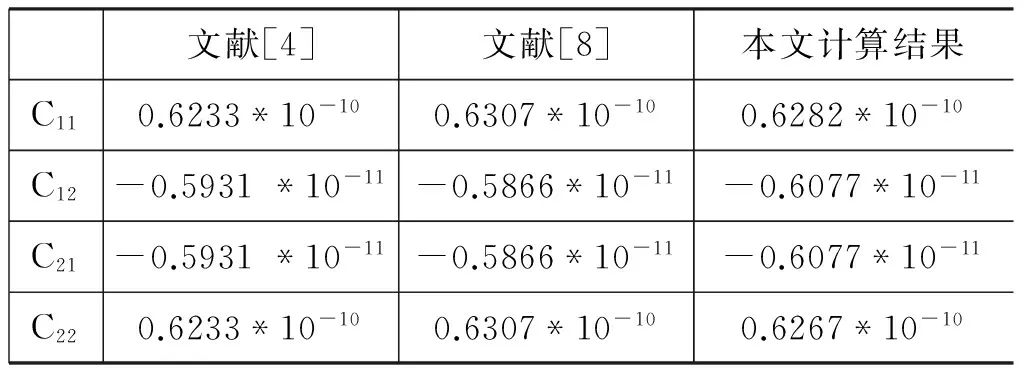
表1　对称耦合微带线的分布电容参数 (F/m)

3.2放置在均匀介质中的两接地平面之间的不对称耦合微带线

图3给出了放置在均匀介质中的两接地平面之间的不对称耦合微带线横截面结构。将位于左侧的微带线视作端口1，右侧的微带线视作端口2。两条微带线厚度均为0.001mm，宽度为3mm，微带线之间距离为2mm，端口1与底层地平面的距离为1mm，端口2与底层地平面的距离为0.5mm，介质的相对介电常数εr为9.5，两地平面之间距离H分别为3mm和5mm。将端口1作为输入端口，计算可得到图4、图5所示的该耦合微带线模型的二维表面电势分布，其中图4为H=3mm时的表面电势分布图，图5为H=5mm时的表面电势分布图。运用有限元方法，计算得到模型的分布电容参数，表2为H=3mm时的分布电容参数，表3为H=5mm时的分布电容参数。通过与文献[3]中的结论对比，误差分别为9.7×10-12F和6.8×10-12F，结果一致性很好。

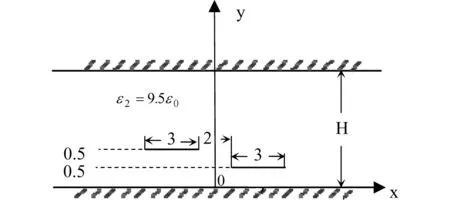
图3　均匀介质中的两接地平面之间的不对称耦合微带线横截面结构

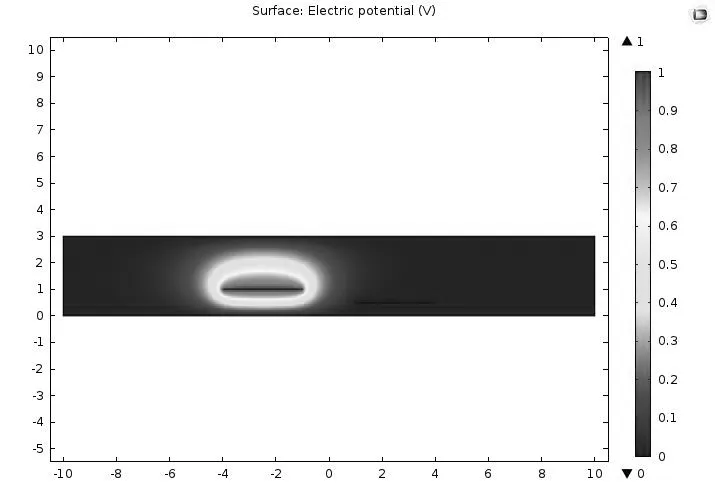
图4　H=3mm时均匀介质中的两接地平面之间的不对称耦合微带线二维表面电势分布

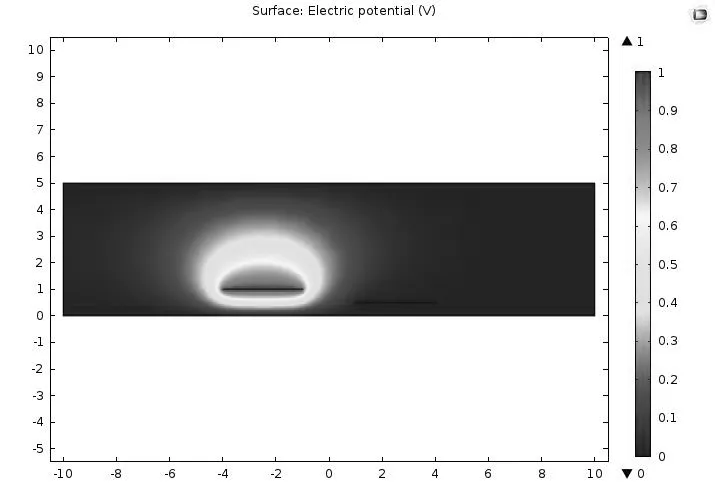
图5　H=5mm时均匀介质中的两接地平面之间的不对称耦合微带线二维表面电势分布

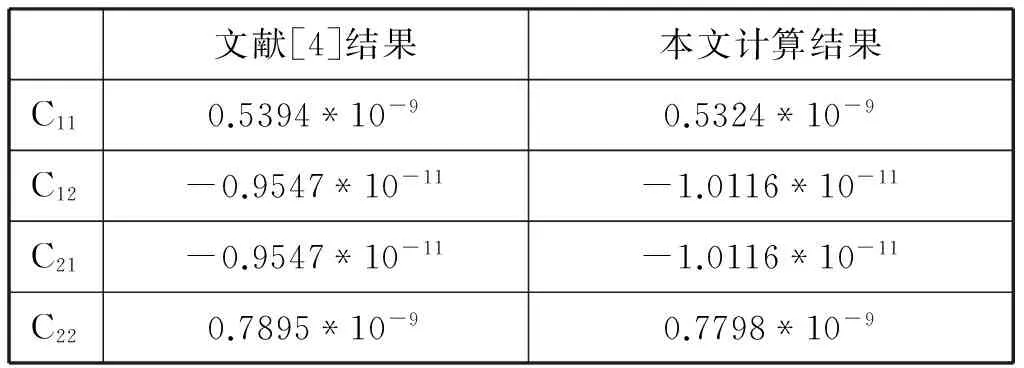
表2　H=3mm时耦合微带线分布电容参数 (F/m)

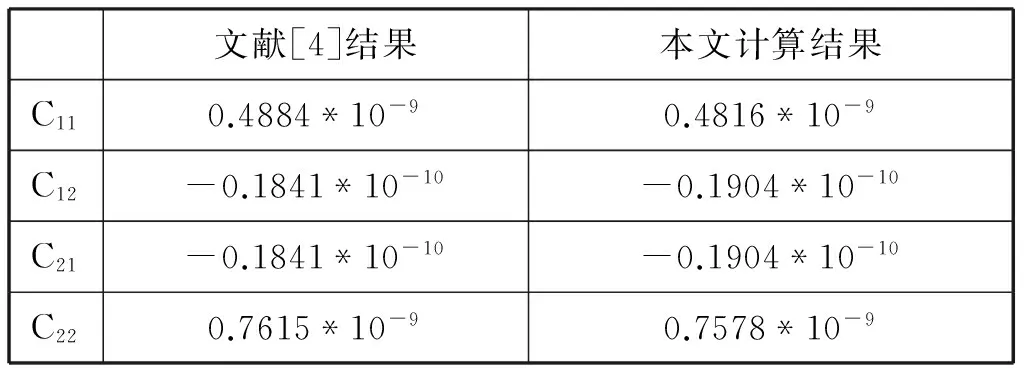
表3　H=5mm时耦合微带线分布电容参数 (F/m)

3.3放置在非均匀介质中的三条耦合微带线

将三条耦合微带线分别放置在两接地平面之间的不同介质层中，分析计算三条耦合微带线的分布电容参数，该模型的横截面结构及其参数如图6所示。此时将位于最左侧的微带线视作端口1，位于中间位置的微带线视作端口2，最右侧的微带线视作端口3。三条微带线厚度均为0.001mm。将端口2作为输入端口后计算得到该模型的二维表面电势分布如图7所示，表4为计算得到的该模型单位长度分布电容参数。通过与文献[4]中的分布电容参数进行比较，发现误差小于7.5×10-12F，方法可行有效。

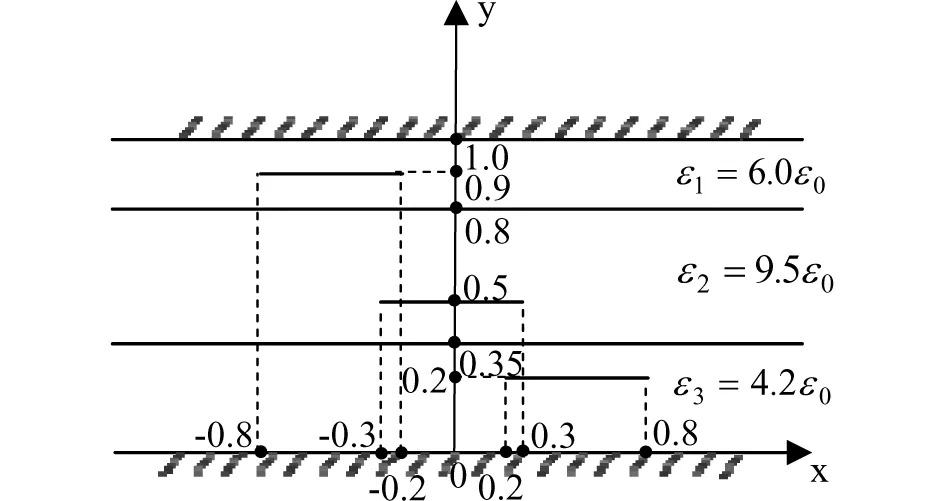
图6　非均匀介质中的三条耦合微带线横截面结构

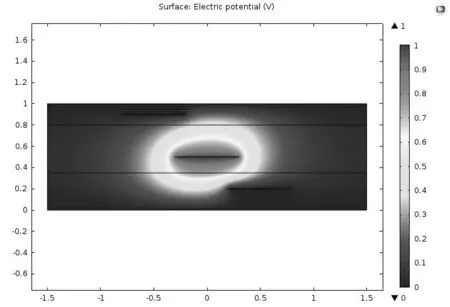
图7　将端口2作为输入时非均匀介质中的三条耦合微带线的二维表面电势分布

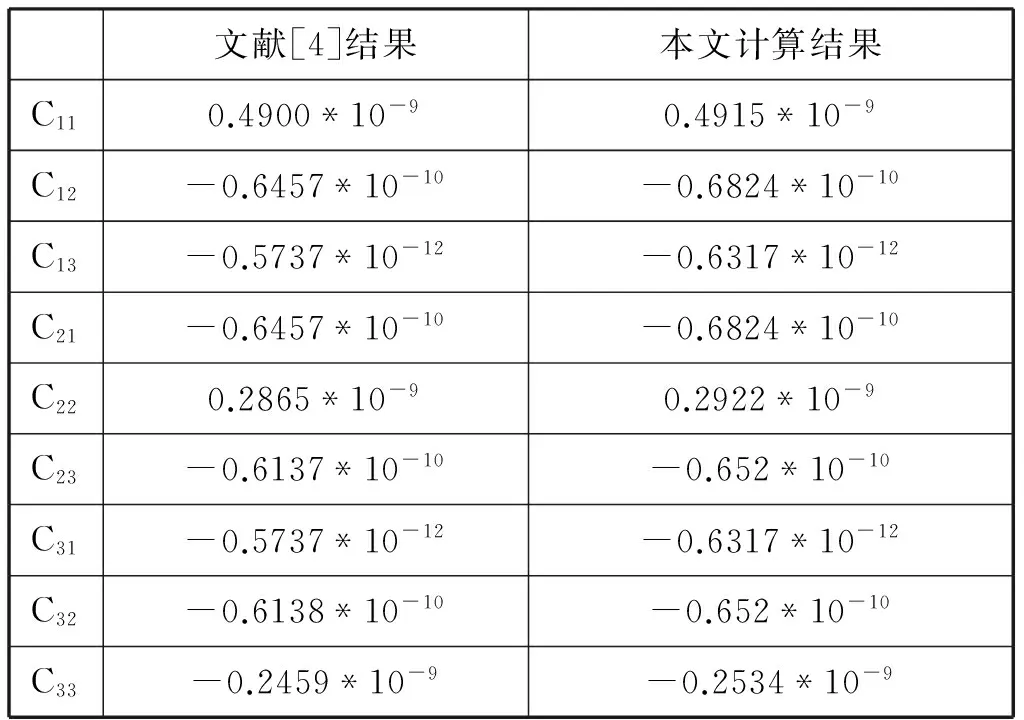
表4　非均匀介质中的三条耦合微带线的分布电容参数 (F/m)

4　结论

耦合微带线之间的串扰问题与其分布参数密切相关。本文采用二维静电环境，对放置在两接地平面之间的两条对称耦合微带线、均匀介质中的两条不对称耦合微带线以及非均匀介质中的三条耦合微带线等三种耦合微带线结构进行了建模，利用有限元方法对三种模型的单位长度分布电容参数进行了计算，并得到了三种耦合微带线模型的二维表面电势分布。将本文计算得到的分布电容参数与相关文献中结论进行对比，发现误差很小，结果一致性很好。因此，有限元方法是一种计算耦合微带线分布参数的有效可行的方法。

[1]Musa S M，Sadiku M N O.Analysis of multiconductor Quasi-TEM transmission lines and multimode waveguides[J].International Journal of Engineering Research and Development，2014，10(3)：87-93.

[2]Musa S M，Sadiku M N O，Obiomon P H.Integrated circuit interconnect lines on lossy silicon substrate with finite element method[J].Journal of Engineering Research and Applications，2014，4(1)：243-247.

[3]Musa S M，Sadiku M N O，Emam A Z.Finite element analysis of integrated circuit interconnect lines on lossy silicon substrate[C].Proceedings of the 2011 COMSOL Conference in Boston，2011.

[4]Cao W，Harrington R F，Mautz J R.Multiconductor transmission lines in multilayered dielectric media[J].IEEE Transmissions on Microwave Theory and Techniques，1984，32(4)：439-450.

[5]Cao W，Harrington R F.Computation of the parameters of multiconductor transmission lines in two dielectric layers above a ground plane[D].Springfield：Department Electrical Computer Eng，Syracuse University，Rep，1982.

[6] Plaza G，Mesa F，Horno M.Quick computation of C，L，G，and R matrices of multiconductorand multilayered transmission systems[J].IEEE Transmissions on Microwave Theory and Techniques，1995，43(7)：1623-1626.

[7]Liu S J，Zhu H Q.An efficient algorithm for the parameter extraction of multiconductor transmission lines in multilayer dielectric media[C].Proceeding of IEEE Antennas and Propagation Society International Symposium，2005：228-231.

[8]WeeksWT.Calculation of coefficients of capacitance of multiconductor transmission lines in the presence of a dielectric interface[J].IEEE Trans Microwave Theory Tech，1970，18(1)：35-43.

(责任编辑：王谦)

Calculating Distributed Capacitance of Coupled Micro-strip Transmission Lines by Finite Element Method

YANG Li，LU Gui-zhen

(Information Engineering School，Communication University of China，Beijing 100024，China)

The Crosstalk between coupled micro-strip lines is closely related to distributed parameters.In this paper，the finite element method is used to calculate the distributed capacitance matrix of coupled micro-strip lines.Threedifferent models are simulated，which are embedded between ground planes，in a homogeneous medium，and in a three-layered dielectric layers.The potential distributions of these models are illustrated，and the distributed capacitance matrices are calculated.The results are compared with those obtained by previous investigators.They are in good agreement，and the method is feasible.

coupled Micro-strip lines；capacitance matrix；the Finite Element Method；electromagnetic compatibility

2016-05-08

杨莉(1977-)，女(汉族)，甘肃省定西市人，中国传媒大学信息工程学院讲师.E-mail：onion@cuc.edu.cn

TM153

A

1673-4793(2016)04-0061-05