广义Agard偏差函数的不等式

张 燕，裘松良

（浙江理工大学理学院，杭州310018）

广义Agard偏差函数的不等式

张 燕，裘松良

（浙江理工大学理学院，杭州310018）

通过对广义Agard偏差函数与一些初等函数组合形式的单调性和凹凸性的研究，获得了广义Agard偏差函数和广义线性偏差函数的最新上下界，从而推广了平面拟共形映射理论中Agard偏差函数与线性偏差函数的一些不等式。

广义Agard偏差函数；单调性；不等式

0 引 言

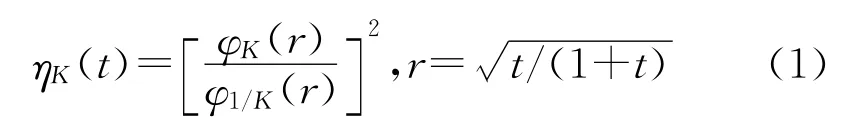
当t=1时，即为线性偏差函数［1］

其中

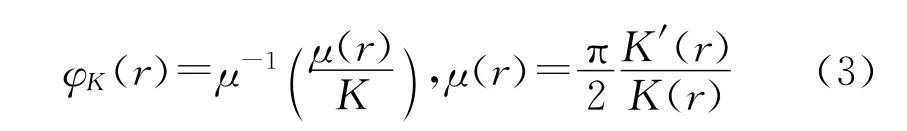
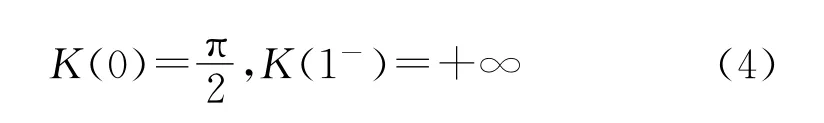
K（r）称为第一类椭圆积分。F（a，b；c；x）为著名的高斯超几何函数［2］，其定义为

下面介绍广义Agard偏差函数［8］，其定义为

当t=1时，即为广义线性偏差函数［8］

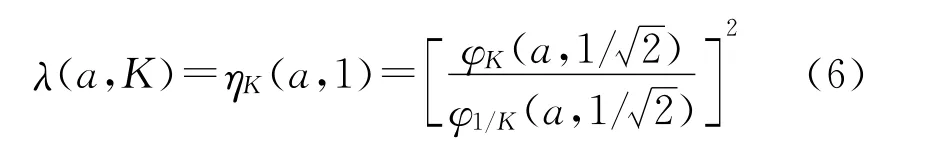
其中

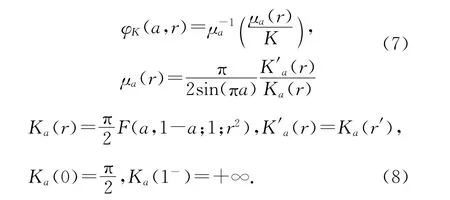
Ka（r）称为第一类广义椭圆积分。显然，ηK（1/2，t）=ηK（t），λ（1/2，K）=λ（K）。

近些年来，研究者们建立了许多关于Agard偏差函数的不等式［1，5，9］。

1997年，Anderson等［1］证明了以下不等式：当K＞1，a=（4/π）K（1/）2，b=a/2时，

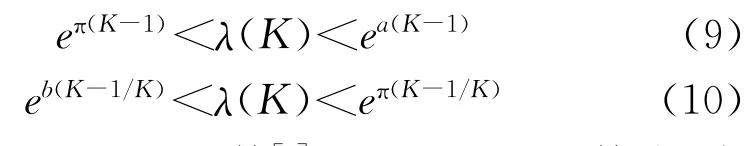
2009年，Anderson等［5］证明了以下不等式：当K＞1，a=（4/π）K（1/）2，b=a/2时，

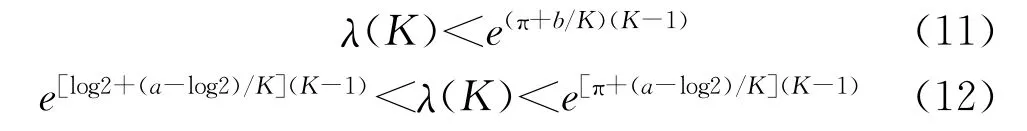
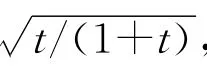
B（r）=8K（r）K′（r）2［E（r）-r′2K（r）］/π2，对所有的K∈（0，∞）成立

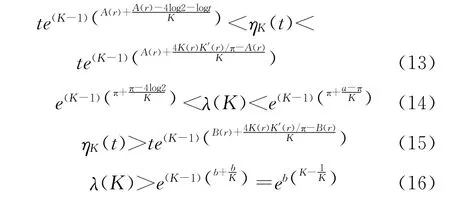
ηK（t）为拟共形映射提供了界，而λ（K）度量了固定无穷远点的上半平面映为自身的K-拟共形映射的边界值的偏差。而Agard偏差函数ηK（t）和线性偏差函数λ（K）分别为广义Agard偏差函数ηK（a，t）和广义线性偏差函数λ（a，K）的特殊情形，因此对于ηK（a，t）和λ（a，K）的研究显得至关重要。本文的主要研究是将式（13）-式（16）进行推广，得到ηK（a，t）和λ（a，K）所满足的一些不等式。

在本文中，我们还需要第二类广义椭圆积分Ea（r）及其Ramanujan常数R（a），它们的定义如下：

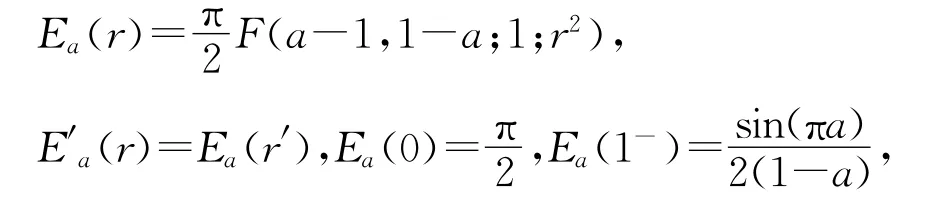
R（a）=-2γ-ψ（a）-ψ（1-a），R（1/2）=log16，其中γ是Euler常数，ψ是经典的Psi函数［7］。

1 主要结果

（1）当c＞P（r）时，Fc从（1，∞）到（-∞，4Ka（r）K′a（r）/［πsin（πa）］-c）严格单调下降；而当c= P（r）时，Fc从（1，∞）到（P（r）-R（a）-log t，4Ka（r）K′a（r）/［πsin（πa）］-P（r））严格单调下降。特别地，当t∈（0，∞）和K∈（1，∞）时，下面的不等式成立：

当t=1时，不等式（17）退化为，

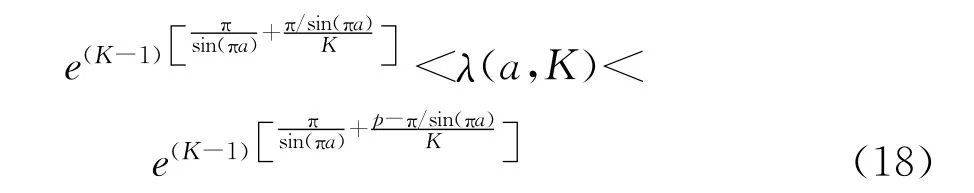
（2）当c≤Q（r）时，Fc从（1，∞）到（4Ka（r）K′a（r）/［πsin（πa）］-c，∞）严格单调下降。特别地，当t∈（0，∞）和K∈（1，∞）时，不等式（19）成立

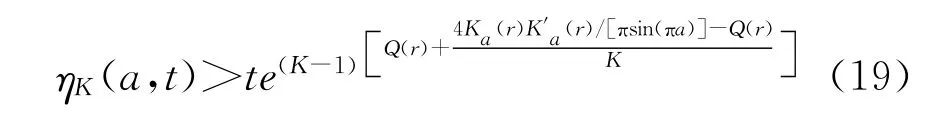
当t=1时，不等式（19）退化为：

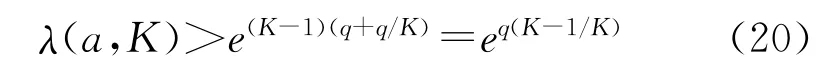
（3）当Q（r）＜c＜P（r）时，存在K1∈（1，∞），使得Fc在（1，K1）上严格单调下降，而在（K1，∞）上严格单调上升。

（4）Fc在（1，∞）上是向下凸的。

2 引 理

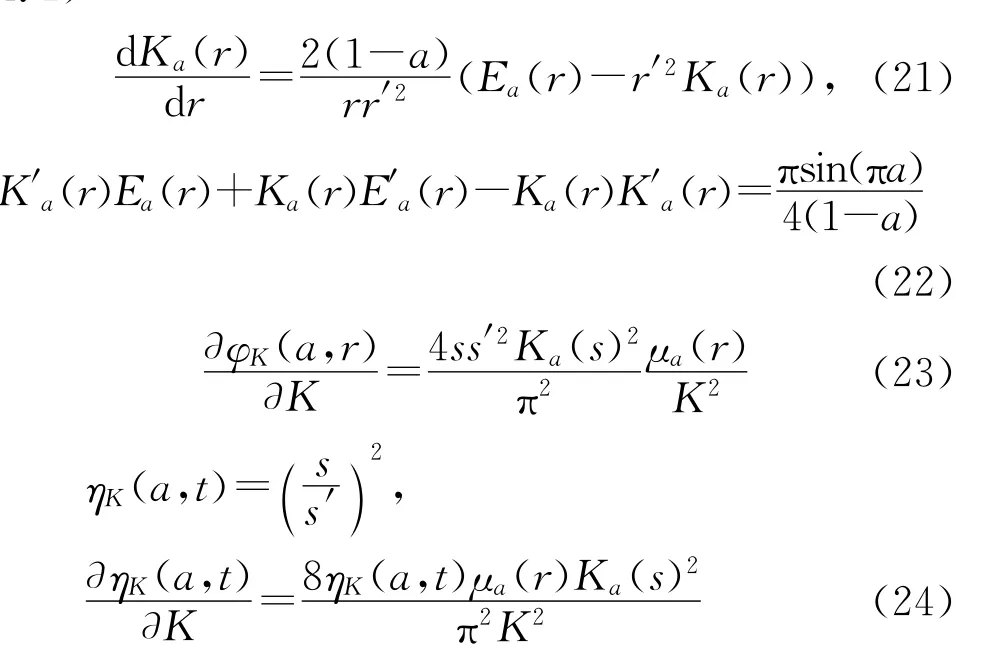
引理2.1（见文献［7］定理1.25）对-∞＜a＜b＜∞，设函数f和g是两个实值函数，并都在［a，b］上连续，在（a，b）上可微且在［a，b］上g′≠0，如果f′/g′在［a，b］上单调上升（下降），那么函数

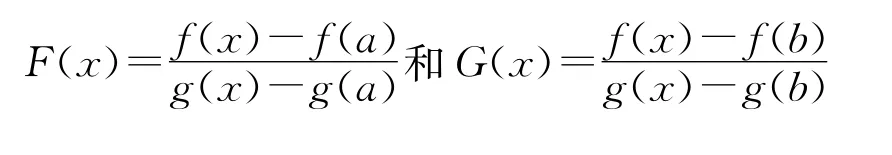
也在（a，b）上单调上升（下降）。而且，若f′/g′的单调性是严格的，则F和G的单调性也是严格的。

如下引理可参见文献［3］中的引理5.2（1）、引理5.4（1）及其定理5.5（2）。

引理2.2对a∈（0，1/2］则有：

（1）（Ea（r）-r′2Ka（r））/r2从（0，1）到（πa/2，sin（πa）/2（1-a））严格单调上升且上凸；

（2）r′cKa（r）从（0，1）到（0，π/2）严格单调下降当且仅当c≥2a（1-a）；

（3）μa（r）+log r从（0，1）到（0，R（a）/2）严格单调下降。

3 定理1.1的证明

定理1.1的证明如下。

对Fc求导，得：

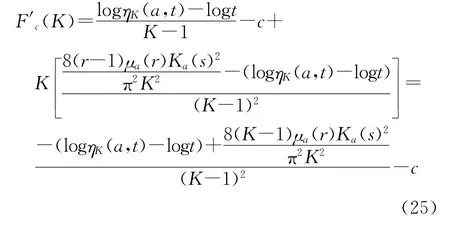
令

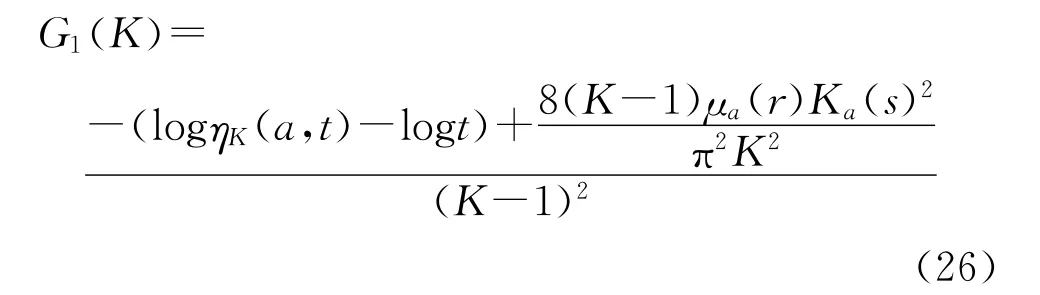
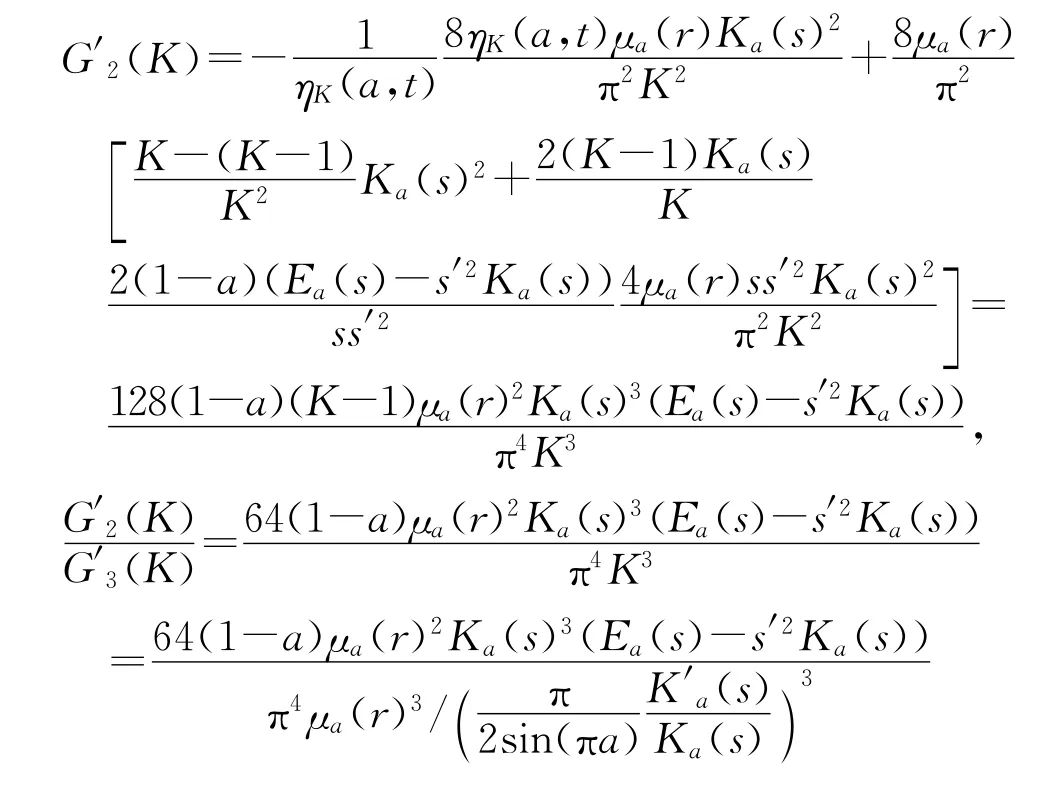
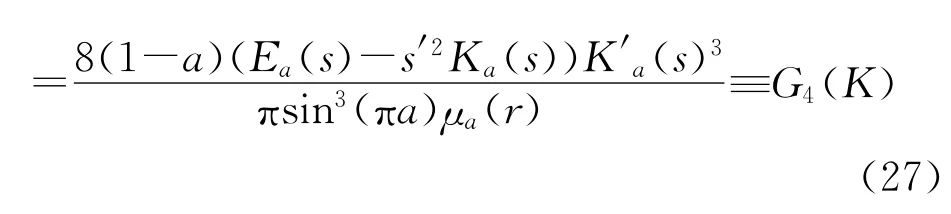
根据引理2.2（1）和（2）可知，G4（K）关于K在（1，∞）上严格单调上升，因此，由式（26）和（27）和引理2.1即可知：G1（K）关于K在（1，∞）上严格单调上升，且

下面逐个证明定理的结论：

（1）当c＞P（r）时，从式（25）、式（28）和G1（K）的单调性即可得到：当K∈（1，∞）时有F′c（K）＜0，从而Fc在（1，∞）上严格单调下降，且

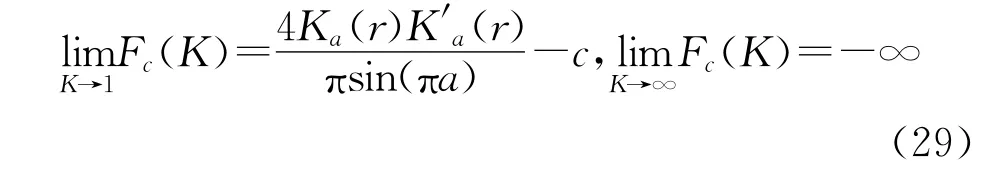
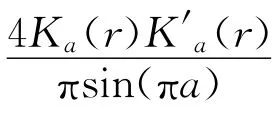
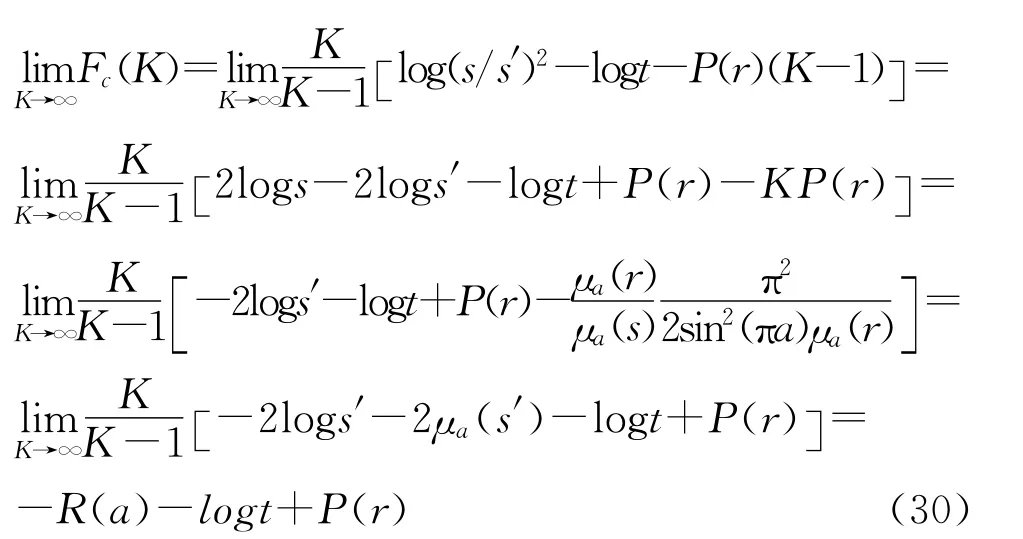
不等式（17）和（18）可由式（29）、式（30）以及此情况下Fc的单调性得到。

（2）当c≤Q（r）时，同样从式（25）、式（28）和G1（K）的单调性即可得到：当K∈（1，∞）时有F′c（K）＞0，从而Fc在（1，∞）上严格单调上升，且

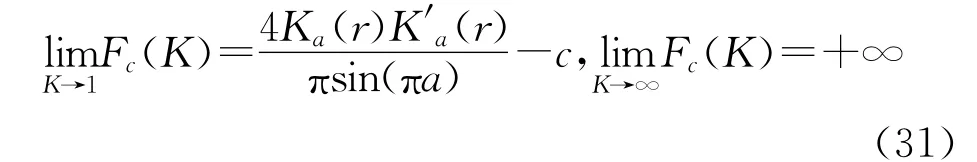
不等式（29）和（30）可由式（31）以及此情况下Fc的单调性得到。

（3）当Q（r）＜c＜P（r）时，同样从（25），式（28）和G1（K）的单调性可知：存在K1∈（1，∞），使得当K∈（1，K1）时，F′c（K）＜0；当K∈（K1，∞）时，F′c（K）＞0。因此，Fc（K）在（1，K1）上严格单调下降，而在（K1，∞）上严格单调上升。

（4）由G1（K）在（1，∞）的单调性便知：Fc在（1，∞）上向下凸的。

推论3.1设p、q为定理1.1所定义的变量，则函数fc（K）=K［logλ（a，K）/（K-1）-c］具有以下性质：

（1）当c＞π/sin（πa）时，fc从（1，∞）到（-∞，p-c）严格单调下降；而当c=π/sin（πa）时，fc从（1，∞）到（π/sin（πa）-R（a），p-π/sin（πa））严格单调下降；

（2）当c≤q时，fc从（1，∞）到（p-c，∞）严格单调上升；

（3）当q＜c＜π/sin（πa）时，存在K2∈（1，∞），使得fc在（1，K2）上严格单调下降，而在（K2，∞）上严格单调上升；

（4）fc在（1，∞）上是向下凸的。

证将t=1代入定理1.1即可得结论。

推论3.1设p，q为定理1.1所定义，对所有的K∈（1，∞）成立不等式：

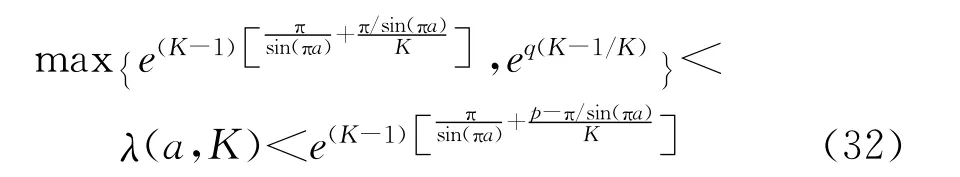
从不等式（18）和（20）即得不等式（32）。

［1］Anderson GD，Vamanamurthy M K，Vuorinen M.Conformal invariants，inequalities，and quasiconformal maps［M］. New York：John Wiley&Sons，1997：1-326.

［2］Bowman F.Introduction to elliptic function with applications［M］.New York：Dover Publications，1953：1-115.

［3］Lehto O，Virtanen K I.Quasiconformal Mappings in the Plane［M］.New York：Springer-Verlag，1973：1-246.

［4］Martin G J.The distortion theorem for quasiconformal Schottky’s theorem and holomorphic motions［J］.Proc Amer Math Soc，1997，125（4）：1095-1103.

［5］Anderson G D，Qiu S L，Vamanamurthy M K，et al. Generalized elliptic integrals and modular equations［J］. Pacific J Math，2000，192（1）：1-37.

［6］Qiu S L.Agard’sη-distortion function and Schottky’s theorem［J］.Sci.China，1997，40（A）：1-9.

［7］Qiu S L，Vuorinen M.Special function in geometric function theory［M］//Handbook of Complex Analysis：Geometric Function Theory.Amsterdam：Elsevier Sci B.V，2005：621-659.

［8］Anderson G D，Qiu S L，Vuorinen M.Modular equations and distortion functions［J］.Ramanujan J，2009，18（20）：147-169.

［9］Chu Y M，Wang M K，Jiang Y P，et al.Monotonicity，convexity，and inequalities involving the Agard distortion function［J/OL］.Abstr Appl Anal，2011.［2013-12-19］. http：//www.hindowi.com/journals/aaa/2011/671765.

InequaIities of GeneraIized Agard Distortion Function

ZHANGYan，QIUSong-liang
（School of Science，Zhejiang Sci-Tech University，Hangzhou 310018，China）

By studying the monotonicity and convexity of the generalized Agard Distortion function and combination forms of some elementary functions，we obtain the latest upper and lower bounds for the generalized Agard Distoriton function and the generalized linear Distoriton function and then extend some inequalities of Agard Distoriton function and linear Distoriton function in the quasiconformal mapping theory.

generalized Agard Distortion function；monotonicity；inequality

O174

A

（责任编辑：康 锋）

1673-3851（2014）05-0555-04

2013-12-19

国家科技支撑项目（11171307）

张 燕（1989-），女，浙江绍兴人，硕士研究生，主要从事拟共形理论、解析函数、特殊函数方面的研究。