第一性原理研究Mn重掺杂对β-Ga2O3的电子结构和光学性能的影响

王国锋，李延杰，钟丹霞，王顺利，崔 灿，李培刚

（浙江理工大学光电材料与器件中心，杭州310018）

第一性原理研究Mn重掺杂对β-Ga2O3的电子结构和光学性能的影响

王国锋，李延杰，钟丹霞，王顺利，崔 灿，李培刚

（浙江理工大学光电材料与器件中心，杭州310018）

采用基于密度泛函理论的第一性原理研究了Mn重掺杂对β-Ga2O3物理性能的影响。建立了β-Ga2O3模型，用Mn原子部分替代Ga原子构建Ga2-xMnxO3的超胞模型，实现对β-Ga2O3的掺杂，分别对x等于0.0625、0.125和0.25的模型进行了几何结构优化，获得稳定的晶格结构和晶胞参数，并对它们的能带结构、态密度和光学性能等进行分析。计算结果表明：Mn掺杂后，禁带宽度减小，费米能级上移进入导带，增大了载流子浓度，提高了体系的电导率；介电函数的虚部有明显的变化；β-Ga2O3在400～700 nm的范围内，吸收系数和反射率均有不同程度的降低，与未掺杂的β-Ga2O3相比，能量损失谱的峰值发生了红移。

β-Ga2O3；能带结构；光学性能；第一性原理

0 引 言

Ga2O3是直接带隙半导体氧化物，由于其禁带宽度较宽，所以响应波段在深紫外区，因而在场致发光、深紫外发光二极管和日盲探测器等方面有着潜在应用，受到了广泛关注。迄今为止，Ga2O3被确定的晶型有5种，分别为α-Ga2O3、β-Ga2O3、γ-Ga2O3、δ-Ga2O3和ε-Ga2O3，其中，β-Ga2O3是已知的最稳定的结构［1］。由于晶格中存在的氧空位，β-Ga2O3呈现出n型半导体的特性，禁带宽度为4.9 eV，是目前已知的透明导电氧化物（TCO）材料中带隙最大的一种材料［2］，已应用于半导体器件的单晶基底、深紫外（DUV）日盲探测器和场效应管等［3-5］。

近年来，对于Ga2O3材料的研究由开始的单一薄膜制备向掺杂转变，因为通过适量掺杂有望解决透明与导电的对立问题，并且掺杂有助于其它相Ga2O3的稳定，如Matsuzaki等［6］将Sn掺杂到Ga2O3中，成功地在α-Al2O3基底上生长出ε-Ga2O3外延薄膜；Hayashi等利用脉冲激光技术，将Mn掺杂到Ga2O3中，首次在MgAlO4单晶基片上外延生长出γ-Ga2O3薄膜［7］。在理论方面，Pei等［8］利用第一性原理分析了Mn掺杂的β-Ga2O3的磁性能；Yang等［9］分析了N、Zn共掺杂的β-Ga2O3的能带结构和光学性能；He等［10］通过计算β-Ga2O3的自旋极化特性，分析了β-Ga2O3的能带结构和分态密度，讨论了Cr、Mn、Ni掺杂后β-Ga2O3的铁磁性。这些研究结果都表明，掺杂对Ga2O3的结构和物理性能有着巨大的影响。

已有实验证明，Mn掺杂能够调制β-Ga2O3的禁带宽度，影响β-Ga2O3薄膜的光学性能［11］，这表明通过掺杂可以调控材料的光学响应波段。因此，β-Ga2O3薄膜在不同波长的紫外滤光器件制造方面有着应用潜力。本文以β-Ga2O3为研究对象，通过用Mn原子部分替代Ga原子的方式来实现对Ga2O3的掺杂，利用第一性原理研究Mn掺杂对Ga2O3的电子结构和光学性能的影响规律，分析了β-Ga2O3掺Mn后相关性质改变的内在原因，以期为实验研究提供相关的理论依据。

1 模型构建和计算方法

1.1 模型构建

β-Ga2O3是单斜晶系，对称性为C2H-3，属于C12/M1空间群，晶格常数为a=1.223 nm，b= 0.304 nm，c=0.58 nm，α=γ=90°，β=103.7°［12］。根据这些参数，本文建立了β-Ga2O3单胞和3种不同掺杂量的Ga2-xMnxO3（x等于0.0625、0.125或0.25）超胞模型。对应的原子个数百分比分别为0、3.125%、6.25%和12.5%。图1为β-Ga2O3的结构示意图，选中的原子即为单胞中要取代的目标原子，由于是原子替代式掺杂，所以对β-Ga2O3的结构没有相变的影响。

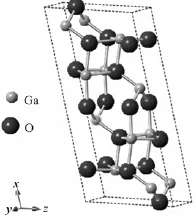
图1 β-Ga2O3结构（选中原子表示要替代的目标原子）

1.2 计算方法

文中所有的计算工作都采用Castep软件包进行［13］。Castep是基于第一性原理，利用分子动力学和密度泛函理论（DFT）作为约束条件的软件包，适用于具有周期性结构的晶体材料，并使用局域密度近似（LDA）或广义梯度近似（GGA）来校正电子之间的交互关联能［14-15］。本文使用GGA的Perdew-Burker-Ernzerhof（PBE）赝势方法处理电子之间的交互关联能。首先对模型进行几何结构优化，得到最优结构后再对它的相关性能进行分析。选取的O、Ga、Mn的原子组态分别为2s22p4、3d104s24p1、3d54s2，所选的赝势为超软赝势。结构优化是在不固定任何参数的情况下进行的，截断能设为380 eV，自洽收敛能精度为平均5.0×10-6eV· atom-1，作用在每个原子上的力不大于0.02 eV· nm-1，内应力不大于0.02 GPa，公差偏移为5.0× 10-5nm，K点取值2×8×4，计算在倒易空间进行。

2 计算结果及分析

2.1 晶体结构和稳定性分析

掺杂前后各个模型的晶格参数和总能量见表1。由表1可知，β-Ga2O3掺杂后，原体系的对称性被破坏，系统无序性增强，体系的总能量降低。由量子力学的能量最低作用原理可知，能量越低，体系越稳定，因此，Ga1.9375Mn0.0625O3的稳定性要比β-Ga2O3要高。对称性变化后，经过结构优化，体系的体积也有所减小。

纵向比较掺杂后的三个体系发现，随着掺杂量的增加，体系的体积逐渐变大，总能量也越来越大。可能的原因是：第一，Mn2+的离子半径为0.08 nm，略大于Ga3+的离子半径0.062 nm，当离子半径大的Mn2+取代离子半径小Ga3+时，根据量子化学理论，掺杂后的β-Ga2O3体系的体积应当有所增加；第二，一个Mn2+取代一个Ga3+时，会产生了一个电子，电子之间的库伦力相互作用导致体系体积增大。随着掺杂量的增加，体系总能量逐渐增大，稳定性逐渐下降。

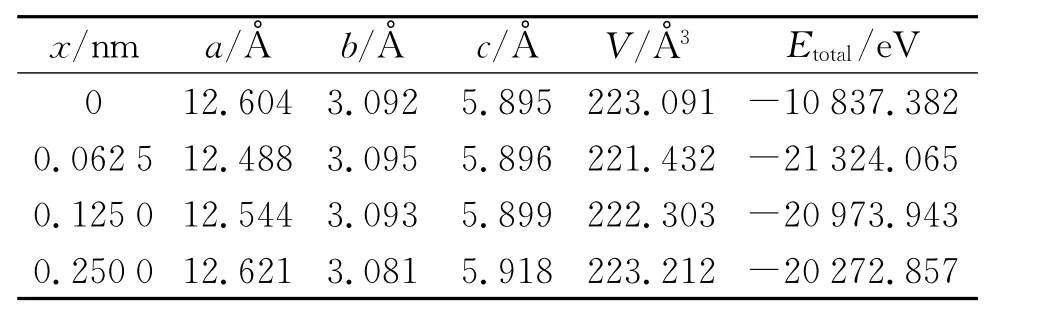
表1 结构优化后各模型的晶格常数，体积和体系总能量

2.2 能带结构和态密度分析

图2是各体系的能带结构图。由于结构的性质通常都是由费米能级附近的能带的变化情况决定的，为了便于比较，图中只给出了能量从-7～8 eV部分的能带结构，其中，纵坐标为0的虚线位置为费米能级处。图2（a）为β-Ga2O3的能带结构图，图中能带的价带顶和导带底都位于同一点---G点，这与直接带隙半导体的性质相符合，因此β-Ga2O3是直接带隙半导体。计算得到的带隙宽度为1.896 eV，这个值与文献中的结果相吻合［16］，但它远小于β-Ga2O3的实际禁带宽度4.9 eV，这主要是因为在用密度泛函理论计算晶体结构时，禁带宽度的大小往往都偏低。具体到本实验，因为模型中Ga 3d态的能量被过高估计［17］，使得它与O 2p态之间的相互作用增强，导致价带上移，致使带隙变窄，这是GGA近似带来的结果［18］。但是本文研究的是相同物理量之间相对值的比较分析，所以这并不影响对β-Ga2O3的电子结构和相关性能的分析。图2（b）和（c）的导带底和价带顶都在G点，但是图2（d）中导带顶和价带底的位置已经发生偏离，说明过度掺杂的β-Ga2O3不是直接带隙半导体，这可能是掺杂的浓度过大（一个晶胞内包含一个杂质原子）导致晶体结构和电子结构发生了改变，因此它不再适合与β-Ga2O3进行性能比较。x值为0.062 5和0.125时，价带位置变化不大，如图2（b）和（c）所示，但是，当x值为0.125时，导带更平滑，所以，Ga1.875Mn0.125O3的费米能级要高于Ga1.9375Mn0.0625O3的费米能级，甚至已经进入导带，随着掺杂量的增加，禁带宽度逐渐减小，这个结果和实际实验得到的结果是一致的［11］。图2（b）和（c）中所示的禁带宽度分别为1.747 eV和1.697eV，这是因为掺杂大大增加了载流子的数量，使得费米能级上升，软件自动将纵坐标为0处固定为费米能级，因此，费米能级上升的形式表现为价带和导带同时下降。重掺杂使得导带底附近的量子态基本被电子所占据，发生了载流子简并，这种行为主要发生在高掺杂半导体中（杂质浓度数量级大于或等于1018cm-3的半导体被认为是高掺杂半导体），Ga1.9375Mn0.0625O3的杂质浓度已经高于1018cm-3，属于重掺杂半导体，这也验证了高掺杂半导体简并化的理论。比较图2中所示的4个能带结构图，可以发现，Mn的掺杂在禁带中引入了杂质能级，掺杂量越大，杂质能级数量越多。在图2（d）所示的能带结构中，虽然杂质能级最多，载流子浓度最大，但是由于价带位置大幅度下降，反而使得禁带宽度有所增加，这可能是由于掺杂浓度过大，晶体结构可能已经不是最稳定的状态，所以我们只讨论掺杂浓度在10%以下的体系。

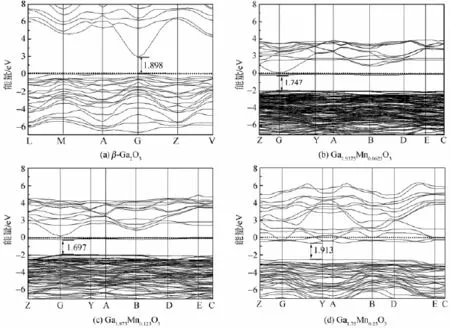
图2 Mn掺杂前后β-Ga2O3的能带结构

图3为掺杂前后β-Ga2O3的总态密度（TDOS）和单个原子的分态密度（PDOS）图。由图3（a）所示的纯相β-Ga2O3态密度图可以看出，β-Ga2O3的价带由三部分组成：上价带-6.7～0.3 eV，这一部分主要是由少量的Ga 4s，Ga 4p和O 2p轨道耦合而成；中间价带-13.5～-11 eV，主要是由Ga 3d轨道和部分O 2s和O 2p轨道耦合而成，最下方的价带-19～-16 eV，这一部分基本是由O 2s态组成的。而导带部分则主要是由Ga 4s、Ga 4p态和O 2p态构成。这和β-Ga2O3的总态密度是相吻合的。图3（b）、（c）和（d）给出了掺杂后的β-Ga2O3的TDOS和PDOS图，结合这3幅图，可以发现，掺杂后，价带和导带都下降，随着掺杂量的增加，下降的幅度变大，进入费米能级以下的导带部分也越多。相比于本征态，掺杂之后，Ga和O的单个原子的态密度有一定的增加，同时轨道的态密度也都向低能方向发生了移动。尤其以O 2p轨道电子的态密度移动的最为显著，它是影响体系导带底和价带顶的重要部分，它的变化和体系的性能息息相关。O 2p轨道的移动是形成n型简并半导体的主要原 因。这和前面对能带结构的分析结果一致。

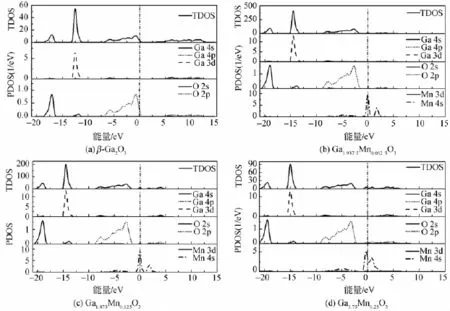
图3 Mn掺杂前后的β-Ga2O3的态密度

2.3 光学性能的研究

光的复介电函数ε（ω）=ε1（ω）+iε2（ω）可以作为固体宏观光学在线性响应范围内的响应函数。其中ε1=n2-k2是虚部，ε2=2nk为介电函数的实部。通过直接跃迁概率的定义和Kramers-Kronig色散关系可以推导出实部ε1，虚部ε2，晶体的吸收系数I（ε）以及能量损失L（ε）和反射系数R（ε）等。以下是相关的变量的直接结果［19］：

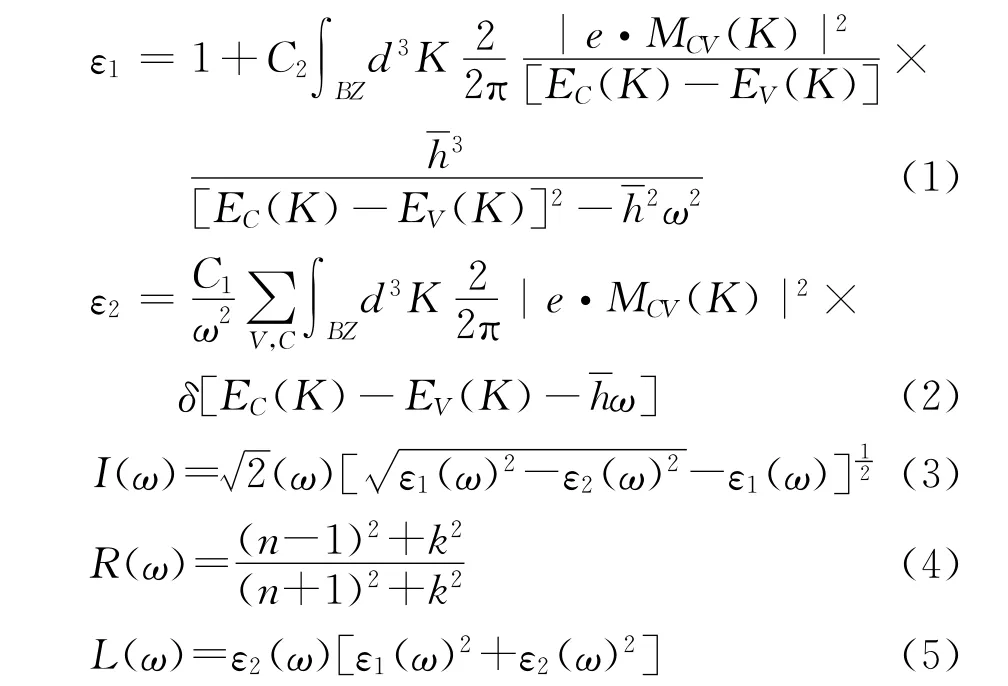
上述式子中，BZ表示第一布里渊区，C和V分别表示导带和价带，ω是角频率，K为倒格矢，代表狄拉克常量，｜e·MCV（K）｜2表示动量矩阵元。上述公式可以用来分析晶体的光学性质，讨论其产生光谱的发光机理。

图4（a）给出了纯相和掺杂后的β-Ga2O3的介电常数的实部和虚部对比。可以看到纯相的β-Ga2O3的虚部有2个峰，分别在8.48 eV和23.47 eV附近，这两个峰主要是由O 2p和Ga 4p以及O 2p和Ga 3d轨道之间的电子跃迁造成的［20］，当x= 0.062 5时，曲线向低能方向大幅移动，峰值变小，在0.1 eV附近增加了一个峰，当x=0.125时，曲线存在4个峰，分别位于0.25、4.8、7.7、19.6 eV附近，新峰的出现主要是受Mn 3d轨道电子的影响。随着掺杂浓度的增大，最大峰值逐渐增大，向高能方向移动，这和Mn 3d轨道量子态随着浓度增加而增强有关系。介电函数实部的变化情况和虚部类似，随着掺杂浓度的增加，最小值的位置先左移，然后逐渐右移。

图4（b）、（c）和（d）分别给出了吸收谱，反射率和能量损失随掺杂浓度的变化情况。图4（b）是光学吸收谱随掺杂浓度的变化情况，从中可以看出，纯相的β-Ga2O3的吸收谱有两个峰，分别位于13.4 eV和23.87 eV处，最小的光吸收边线性部分与纵坐标的交叉点约为1.9 eV，与图2中所的带隙值相符，各个体系的光最小吸收边在图4（b）内插图给出，这个结果与前面计算的带隙的结果是完全吻合的。与纯相的β-Ga2O3相比，Mn掺杂后的吸收谱在0.9 eV附近多了一个吸收峰，这是由Mn 3d轨道与O 2p轨道之间的电子的光学跃迁引起的。比较掺杂前后的吸收谱，我们发现：随着掺杂浓度的增加，光学最小吸收边逐渐向低能量方向偏移，发生了红移，这个结果与文献［11］的结论相吻合，这个现象主要是由Burstein-Moss效应导致的［21-22］。掺杂后，β-Ga2O3的费米能级靠近导带，在禁带中出现了杂质能级，随着浓度的增加，能级数量增多，甚至形成能带，使得价带载流子向导带跃迁，价带向低能方向偏移，使得吸收边朝着低能方向移动。掺杂的β-Ga2O3的吸收能量范围比纯相的β-Ga2O3小，而且吸收峰强度明显降低。吸收峰的产生是因为处于激发态的价带电子向导带光学跃迁，吸收峰强度的衰减表明Mn掺杂引入了杂质能级，降低了发生光学跃迁所需的能量。图4（c）给出了掺杂前后β-Ga2O3反射率的变化。纯相的β-Ga2O3的反射峰位置在15.9 eV左右，掺杂后主峰的位置向低能方向移动，但是随着浓度的增加，峰的位置发生蓝移，峰强随着掺杂浓度增高而增大。掺Mn后吸收率和反射率都比纯相的β-Ga2O3要小，这说明掺杂后，模型在紫外光区的透过率增大。能量损失谱是描述电子在通过均匀的电介质时能量损失情况的物理量［23］。图4（d）中，纯相的β-Ga2O3的能量损失峰值在17.72 eV附近，与之相比，掺杂后能量损失谱都发生了红移，而后随着掺杂量的增加，能量损失峰蓝移，峰强逐渐增大，结合光学性质的各曲线，我们发现：能量损失峰的能量位置与吸收谱和反射谱急剧下降位置是相对应的。

图4 Mn掺杂前后β-Ga2O3的光学性能

3 结 论

运用第一性原理的方法研究了Mn重掺杂对β-Ga2O3晶体的能带结构和光学性能的影响。研究发现，Mn的掺杂导致β-Ga2O3导带和价带整体下移，费米能级进入了导带，介电函数实部和虚部在低能部分都小于纯相的β-Ga2O3，光学最小吸收边红移，吸收系数和反射率在可见光区的都有明显的降低，能量损失谱向低能方向移动。通过对计算结果分析，证明了利用Mn掺杂调控β-Ga2O3的性能是可行的，适度的掺杂有利于提高β-Ga2O3的载流子浓度，导电性能变好，而且还提高了β-Ga2O3在可见光区的透过率，这使得β-Ga2O3作为透明导电氧化物材料具有更好的应用潜力。如果进行过度的掺杂，可能会使得晶格发生变形，不再保持β-Ga2O3的结构，性能也会发生很大的改变。

在计算过程中，笔者没有考虑自旋，所以没有得到Mn掺杂是否会使β-Ga2O3具有磁性。具有磁性的透明导电氧化物材料也是人们非常关注的一个研究热点，Mn掺杂对β-Ga2O3的磁学性能的影响有待进一步研究。

［1］Roy R，Hill V G，Osborn E F.Polymorphism of Ga2O3and the system Ga2O3-H2O［J］.Journal of the American Chemical Society，1952，74（3）：719-722.

［2］Tippins H H.Optical absorption and photoconductivity in the band edge ofβ-Ga2O3［J］.Phys Rev，1965，140（1A）：A316-A319.

［3］Kokubun Y，Miura K，Endo F，et al.Sol-gel prepared β-Ga2O3thin films for ultraviolet photodetectors［J］. Appl Phys Lett，2007，90（3）：031912-031912-3.

［4］Oshima T，Okuno T，Fujita S.Ga2O3thin film growth on c-plane sapphire substrates by molecular beam epitaxy for deep-ultraviolet photodetectors［J］.Jpn J Appl Phys，2007，46：7217-7220.

［5］Oshima T，Okuno T，Arai N，et al.Vertical solar-blind deep-ultraviolet Schottky photodetectors based onβ-Ga2O3substrates［J］.Appl Phys Express，2008，1：011202-011202-3.

［6］Matsuzaki K，Yanagi H，Kamiya T，et al.Field-induced current modulation in epitaxial film of deep-ultraviolet transparent oxide semiconductor Ga2O3［J］.Appl Phys Lett，2006，88（9）：092106-092106-3.

［7］Culebras M，Gómez C M，Cantarero A.Thermoelectric measurements of PEDOT：PSS/expanded graphite composites［J］.Energy Materials&Thermoelectrics，2013，48（7）：2855-2860.

［8］Pei G Q，Xia C T，Dong Y J，et al.Studies of magnetic interactions in Mn-dopedβ-Ga2O3from first-principles calculations［J］.Scripta Mater，2008，58（11）：943-946.

［9］Yang J L，Zhao Y N.Electronic structure and optical properties of N-Zn co-dopedβ-Ga2O3［J］.Sci China Phys Mech Astron，2012，55（4）：654-659.

［10］He H，Li W，Liang E J，et al.First principles study on the electronic properties of Cr，Fe，Mn and Ni dopedβ-Ga2O3［J］.Adv Mater Res，2012，535-537：36-41.

［11］胡 帆，晁明举，梁二军，等.Mn掺杂Ga2O3薄膜的结构及光吸收性能研究［J］.材料导报，2009，23（16）：16-18.

［12］Geller S.Crystal structure ofβ-Ga2O3［J］.J Chem Phys，1960，33（3）：676-684.

［13］Duan W H，Wentzcovitch R M，Thomson K T.Firstprinciples study of high-pressure alumina polymorphs［J］.Phys Rev B，1998，57（17）：10363-10369.

［14］Vanderbilt D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism［J］.Phys Rev B，1990，41（11）：7892-7895.

［15］Perdew J P，Burke K，Ernzerhof M.Generalized gradient approximation made simple［J］.Phys Rev Lett，1996，77（18）：3865-3868.

［16］Yamaguchi K.First principles study on electronic structure ofβ-Ga2O3［J］.Solid State Commun，2004，131（12）：739-744.

［17］He H Y，Blanco M A，Pandey R.Electronic and thermodynamic properties ofβ-Ga2O3［J］.Appl Phys Lett，2006，88（26）：261904-261904-3.

［18］Robertson J，Xiong K，Clark S J.Band structure of functional oxides by screened exchange and the weighted density approximation［J］.Phys Status Solidi B，2006，243（9）：2054-2070.

［19］沈学础.半导体光学性质［M］.北京：科学出版社，1992：24.

［20］He H Y，Orlando R，Blanco M A，et al.First-principles study of the structural，electronic，and optical properties of Ga2O3in its monoclinic and hexagonal phases［J］.Phys Rev B，2006，74（19）：195123-195123-8.

［21］Lu JG，Fujita S，Kawaharamura T，et al.Carrier concentration induced band-gap shift in Al-doped Zn1-xMgxO thin films［J］.Appl Phys Lett，2006，89（26）：262107-262107-3.

［22］Lin J M，Zhang Y Z，Ye Z Z，et al.Nb-doped ZnO transparent conducting films fabricated by pulsed laser deposition［J］.Appl Surf Sci，2009，255（13/14）：6460-6463.

［23］段满益，徐 明，周海平，等.过渡金属与氮共掺杂ZnO电子结构和光学性质的第一性原理研究［J］.物理学报，2007，56（9）：5359-5365.

Study of Effects of Heavy Mn Doping on EIectronic Structure and OpticaI Property ofβ-Ga2O3with the First PrincipIe

WANG Guo-feng，LI Yan-jie，ZHONG Dan-xia，WANG Shun-li，CUI Can，LI Pei-gang
（Center for Optoelectronics Materials and Devices，Zhejiang Sci-Tech University，Hangzhou 310018，China）

This paper adopts the first principle based on Density Functional Theory to study heavy Mn doping on physical properties ofβ-Ga2O3and establishes ofβ-Ga2O3model.Mn atom replaces Ga atom to construct super-cell model of Ga2-xMnxO3to realizeβ-Ga2O3doping.Geometric structure optimization is conducted for the models with x=0.062 5，0.125，0.25.Stable crystal structure and crystal cell parameters are gained.Besides，their energy band structure，state density and optical properties are analyzed. The results show that after Mn doping，energy band width decreases；Fermi level moves up and enters the conduction band；carrier concentration increases；conductivity of the system rises；the imaginary part of dielectric function has obvious changes；absorption coefficient and reflectivity ofβ-Ga2O3within 400～700 nm reduce to different degrees.Compared with non-dopedβ-Ga2O3，the peak value of energy loss spectrum presents red-shift.

β-Ga2O3；energy band structure；optical property；the first principle

O469，O471.5

A

（责任编辑：康 锋）

1673-3851（2014）05-0586-07

2013-12-13

国家自然科学基金（61274017，11074220，51072182，51172208）；浙江省大学生科技创新活动计划（2013R406041）；浙江省钱江人才计划（QJD1202004）

王国锋（1986-），男，河南信阳人，硕士研究生，主要从事纳米材料测量的研究。

李培刚，E-mail：peigangli@163.com