复模糊微分方程的初始值问题
吴 丹,韩 维,樊太和
(浙江理工大学科学计算与软件工程实验室,杭州310018)
复模糊微分方程的初始值问题
吴 丹,韩 维,樊太和
(浙江理工大学科学计算与软件工程实验室,杭州310018)
复模糊微分方程的初始值问题是近年来研究的热点问题。首先证明了复模糊域上的牛顿-莱布尼茨公式,并建立了微分和积分之间的关系,然后定义了复模糊微分方程的初始值问题,最后给出了基于经典的不动点定理和基于Zadeh在复数域上的扩展原理两种初始值问题存在的结论。然后在此基础上对初始值进行求解。
复模糊微分方程;初始值问题;牛顿-莱布尼茨公式;Zadeh扩展原理
0 引 言
复微分方程已经在很多领域得到了应用,例如Gilboa等[1]通过结合扩散方程和简化的Schrodinger方程来进行图像处理;Takac等[2]将复Ginzburg-Landau equation应用在动力学上等。这些应用都是基于初始值和参数值易脆的假设下进行的,但是在许多应用中,由于复数表示的参数具有模糊性,因此,这些由复数表示参数的方程都具有模糊的特点。这类由复数作为参数的方程可用模型p′=f(t,p)表示,其中,t∈T=[a,b]⊂(-∞,+∞),T→表示广义复模糊数的集合,f∶T×→。这个模型称为复模糊方程。下面研究该模型的初始值问题:

其中,p0∈。这种解不稳定的情况,称为复模糊数域中的初始值问题。初始值问题的解可由下式表示:

其中积分和微分是采用Buckley等[3-4]所给的定义。
本文首先建立复模糊数域上的牛顿-莱布尼茨公式,建立复模糊数域上的积分和微分的联系,使得在复模糊数域上定义初始值问题成为可能;然后通过两种方法来证明初始值问题的解的存在性,第一种是基于经典不动点定理的方法,第二种是基于Zadeh在复模糊数域上的扩展原理的方法。比较初始值问题的模糊微分方程[5-14],得出在复模糊数域的情况下,由于积分路径是独立的,所以初始值问题需要强有力的条件;在这个基础上,本文展开了对复模糊微分方程初始值问题的研究。
1 一些基本定义和结果

接下来定义广义复模糊数。
定义1[15]一个模糊集合是广义复模糊数,当且仅当
备注:在Wu等[16]、Buckley等[4]的定义中,在(2)中增加了一个额外的条件:“单连通”。然而,Qiu等[15]提出了一个反例:在这个条件下广义复模糊数在基本的算术运算下不是封闭的。
定义2[4]令:f:T→是星形的,f(t)的导数f′(t)是复数集合的模糊子集,并由它的隶属函数定义:μ(z|f′(t))=sup{α|z=x(t,α,β)+iy(t,α,β),0<α≤1,0≤β<2π}。
定理1[15]如果x·和y·在α和β上是连续的,则f′(t)∈。
在复数的情况下,z=x+iy是一个一般复数,令f(z)=(z),对任意的α水平集(z)(α),0<α≤1,画一条射线L(β),在复平面上的x轴正半轴的画一个角度β(0≤β<2π)。考虑到集合L(β)∩(z)(α)=w(z,α,β),f(z)是星形的,当且仅当(z)(α)是一个点。对所有的0<α≤1,0≤β<2π,w(z,α,β)=μ(x,y,α,β)+iv(x,y,α,β)。通过定义w(z,α,0)=w(z,α,2π),可以将这个概念扩展到β=2π,其中假设对所有的0≤β<2π,w1(z)=w(z,1,β)。
令D⊆C是闭的、有界的、单连通的数域,γ是D中的可求曲线,因此γ可以用函数z=φ(l)+iφ(l),a≤l≤b描述,其中φ(l)和φ(l)是[a,b]上的一个实值,所以γ将是D上的平滑曲线。如果g:γ→C,g(z)=μ(x,y)+iv(x,y)其中μ和v是z=x+ iy的实值函数,而且g在D上是连续的,则g在γ上的复线性积分是:

其中φ′(φ′)表示φ(φ)的导数。
定义3[3]令f:γ→,定义g(z)∈(z)(α),0<α≤1 }。f(z)在γ上的模糊线性积分通过它的隶属函数可以定义为复数的模糊子集:

令z=φ(t)+iφ(t)=t+i0,a≤t≤b,可求曲线γ在位于复平面x轴正半轴的区间[a,b]上。γ=T,复模糊映射f:γ→是f(t+i0)=(t),其中(t)可以通过它的α水平集(z)(α)定义,a≤t≤b。
定理2如果f∶T→是连续的,则f(s)d s在T是拉普拉斯连续的。
定理3如果f,g∶T→是可积的,k∈R,则:

(3)∫TH(f(t),g(t))d t存在,并且 (H∫Tf(t)d t,
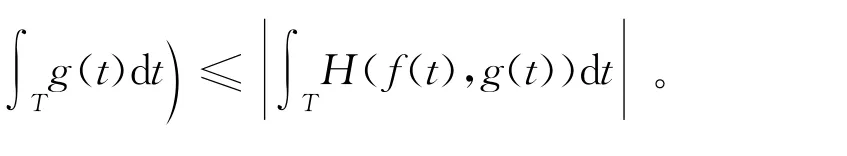
2 复模糊数域上的牛顿-莱布尼茨公式
引理1如果和是连续的,则f′(t)(α)= Γ(α)。
定理4(牛顿-莱布尼茨公式)函数f:T→是星形的,假设和是连续的,在D上由a到b的积分曲线,有
证明:


隶属函数可以表示为:

证毕。
3 复模糊数初始值问题
在C中的任意两个非空完备集合A和B,Hausdorff距离可以定义为:

其中‖.‖表示C中的欧几里德范数。

p′=f(t,p),t∈T,p(a)=p0
从Wu等[16]的定理3中,由∫Tf(t,p(t))d t∈∪积分的紧密度,可得以下的等价描述。
接下来用两种方法来解复模糊初始值问题。
4 通过不动点定理证明解的存在性
考虑问题初始值问题I,(IVP-I)p′=f(t,p),t∈T,p(a)=p0,其中f∶T×C*→C*,p0∈C*,有以下存在的结果。
定理5 假设f满足拉普拉斯条件,D(f(t,p),f(t,q))≤k(t)D(p,q),其中k∶T→R+是可积的,并且∫Tk(t)d t=L<1,问题(IVP-I)有唯一的解。


证毕。
5 通过扩展原理证明解的存在性
在讨论存在性之前,先证明Zadeh的扩展原理在复模糊域上也成立。


对一些un∈f-1(wn)∩(0),由于f-1是闭的,(0)是完备的,则un的一个子序列unk收敛到u0,并且f(u0)=w0。由于μ(u|)是上半连续的,则limμ(unk|)≤μ(u0|)。接下来,

由于wn→w0,于是有limμ(unk|))≤μ(w0|))。

由于当0≤α≤1时,f是连续的,(1)是完备和弧形的,则)(α)也有相同的性质。
在给出(IVP-I)解的存在性之前,首先检查初始值问题在易脆的情况下(IVP-C):
(IVP-C)p′=f(t,p),t∈T,p(a)=p0
其中,f∶T×C→C,p0∈C。假设(IVP-C)在p0∈U上有一个解p(t,p0),其中U是一个开集。于是对所有的t∈T,p(t,·)在U上是连续的,定义如下一个运算:
Lt∶U→C,Lt(p0)=p(t,p0)。
这表明(IVP-C)有唯一解,并且对于p0,Lt是连续的,对Lt应用Zadeh的扩展原理,将得到一个映射∶C→(α)=p(t,p0(α))。这是(IVP -I)的一个精确解。
再来考虑下面这个问题:

其中f(t,p)=λp(t),λ∈C,p0∈。首先,对于p0∈C,该方程的初始确定性解是Lt(p0)= p0eλ(t-a),对于每一个t∈[a,b],方程在p0点处是连续的。最后,结合扩展原理,对所有的p0∈,存在(p0),有(p0)(α)=Lt(p0(α))=p0(α)eλ(t-a)。
6 结论和未来的工作
本文主要研究了复模糊方程的初始值问题,并且得到了一个新的牛顿-莱布尼茨公式,将Zadeh的扩展原理应用到了复模糊数域上,最后得到了初始值问题存在的结论,并对初始值进行了求解。
在以后的工作中,将进一步考虑复模糊微分方程和模糊微分方程的区别,并且研究其他类型的初始值问题,探索其他方法解出初始值问题的解。
[1]Gilboa G,Zeevi Y Y,Sochen N A.Complex Difusion Processes for Image Filtering[M]//Scale-Space and Morphology in Computer Vision.Springer Berlin Heidelberg,2001:299-307.
[2]Takac P,Berg L,Engel W,et al.Dynamics on the attractor for the complex Ginzburg-Landau equation[J].Rostock Math Kollop,1995,49:163-184.
[3]Buckley J J.Fuzzy complex analysis II:integration[J]. Fuzzy Sets and Systems,1992,49(2):171-179.
[4]Buckley JJ,Qu Y.Fuzzy complex analysis I:differentiation[J].Fuzzy Sets and Systems,1991,41(3):269-284.
[5]Oberguggenberger M.Fuzzy and weak solutions to differential equations[C]//Proceedings of the Tenth International Conference IPMU.2004:517-524.
[6]Oberguggenberger M,Pittschmann S.Differential equations with fuzzy parameters[J].Mathematical and Computer Modelling of Dynamical Systems,1999,5(3):181-202.
[7]Seikkala S.On the fuzzy initial value problem[J].Fuzzy Sets and Systems,1987,24(3):319-330.
[8]Song S,Wu C.Existence and uniqueness of solutions to Cauchy problem of fuzzy differential equations[J].Fuzzy Sets and Systems,2000,110(1):55-67.
[9]Ma M,Friedman M,Kandel A.Numerical solutions of fuzzy differential equations[J].Fuzzy Sets and Systems,1999,105(1):133-138.
[10]Nieto J J.The Cauchy problem for continuous fuzzy differential equations[J].Fuzzy Sets and Systems,1999,102(2):259-262.
[11]Kaleva O.A note on fuzzy differential equations[J]. Nonlinear Analysis:Theory,Methods&Applications,2006,64(5):895-900.
[12]Kaleva O.Fuzzy differential equations[J].Fuzzy Sets and Systems,1987,24(3):301-317.
[13]Kaleva O.The Cauchy problem for fuzzy differential equations[J].Fuzzy Sets and Systems,1990,35(3):389-396.
[14]Bede B,Rudas I J,Bencsik A L.First order linear fuzzy differential equations under generalized differentiability[J].Information Sciences,2007,177(7):1648-1662.
[15]Qiu D,Shu L,Mo Z W.Notes on fuzzy complex analysis[J].Fuzzy Sets and Systems,2009,160(11):1578-1589.
[16]Wu C,Qiu J.Some remarks for fuzzy complex analysis[J].Fuzzy Sets and Systems,1999,106(2):231-238.
[17]Puri M L,Ralescu D A.Fuzzy random variables[J]. Journal of Mathematical Analysis and Applications,1986,114(2):409-422.
[18]Barros L C,Bassanezi R C,Tonelli P A.On the continuity of the Zadeh’s extension[C]//Proceedings of the IFSA.1997:3-8.
[19]Dubois D,Prade H.Towards fuzzy differential calculus part 1:integration of fuzzy mappings[J].Fuzzy Sets and Systems,1982,8(1):1-17.
[20]Buckley J J.Fuzzy complex numbers[J].Fuzzy Sets and Systems,1989,33(3):333-345.
InitiaI VaIue ProbIem of CompIex Fuzzy DifferentiaI Equations
WU Dan,HAN Wei,FAN Tai-he
(Lab of Intelligent Computing and Software Engineering,Zhejiang Sci-Tech University,Hangzhou 310018,China)
The initial value problem for complex fuzzy equations is a research hotspot in recent years. We first prove Newton-Leibniz Formula on the complex fuzzy domian and establish the relationship between differential and integral.Then,we define initial value problem of fuzzy complex equations and finally give the conclusion that the twp initial values based on classical fixed point principle and Zadeh’s extension principle in complex fuzzy domain have problems.Then,on this basis,we solve the initial value.
complex fuzzy differential equation;initial value problem;Newton-Leibniz formula;Zaden’s extension principle
O175.8
A
(责任编辑:康 锋)
1673-3851(2014)05-0550-05
2014-02-25
国家自然科学基金(61210004)
吴 丹(1987-),女,湖北孝感人,硕士研究生,研究方向为微分方程。

