液柱在激波冲击下RM不稳定性和破裂过程的数值计算

吴 宇，施红辉，王 超，叶 斌，张 珂

（浙江理工大学机械与自动控制学院，杭州310018）

液柱在激波冲击下RM不稳定性和破裂过程的数值计算

吴 宇，施红辉，王 超，叶 斌，张 珂

（浙江理工大学机械与自动控制学院，杭州310018）

对液柱受到激波冲击后在气流中的变形断裂过程进行了数值计算，研究了在该过程中Richtmyer-Meshkov（RM）不稳定性的具体表现。应用Fluent软件，数值模拟了二维（2D）和三维（3D）液柱在激波马赫数为1.10、液柱初始直径为2.76 mm的情况下，气/液界面上RM不稳定性的演化过程以及液体周围的流场。计算结果表明，初始扰动数目对RM不稳定性的影响显著；液柱在横截面平面（Z方向）发生变形失稳，导致沿液柱轴向出现变形失稳。数值计算的结果与已有的实验结果吻合较好。

RM不稳定性；激波；液柱；数值计算

0 引 言

不同形态的液体在激波冲击下失稳与破裂的过程和机理，不但是Richtmyer-Meshkov（RM）不稳定性研究中的一个关键问题，也是一个可压缩性湍流混合问题。液柱在激波以及波后气流冲击下的变形破裂过程中的具体表现与机理，对于进一步研究RM不稳定性有相当重要的意义。2001年，Igra等［1］基于欧拉方程及CIP方法对激波与水柱的相互作用进行了数值计算，并对该方法作了一定程度的改进，使得该算法能够正确地计算出气液界面，而不致使界面处的密度阶跃模糊化，采用该方法的数值计算结果与一些干涉图片有较好的吻合；同时他们对水柱与固体圆柱进行了对比，结果发现，即使是在激波冲击界面40μs后，仍然可观察到液柱和固体圆柱一些差别。2004年，柏劲松等［2］采用可压缩多介质高精度PPM方法对实验模型进行数值计算，对10模峰对峰、峰对谷初始振幅为1 mm的扰动模型在0、320、640、960μs时刻的果冻环进行了计算，结果发现：果冻内外界面变形特征主要表现为Rayleigh-Taylor不稳定性；在爆驱过程中，果冻内界面上的扰动发生反相，并且初始内外界面同相时，初始扰动对后续不稳定性现象的影响更为严重。2008年，Chen等［3］提出了一种带有5分成模型的可压缩多相求解器，对激波与水柱之间的相互作用进行了研究，并计算了平面激波与水柱的相互作用，以及平面激波与双排水柱的相互作用；研究了水柱分别为水平和竖直的两种情况，发现改变放置方向会导致作用过程有差异；使用流动可视化技术展示了激波与水柱相互作用过程中的复杂结构。王涛等［4］提出了基于多相流Volume Fraction（VOF）方法和逐段抛物线方法（piecewise parabolic method，PPM）的多相流逐段抛物线方法（multi-fluid piecewise parabolic method，MFPPM），并对高压气体冲击作用下的气体/液体交界面上的Richtmyer-Meshkov（RM）不稳定性及其引起的流体混合现象进行了数值计算，计算结果表明：流体混合区和尖钉的发展受初始扰动的影响极大，并且该影响在后期更为显著；气泡的宽度随时间线性增长，也略微的受到初始扰动的影响；网格的尺寸不影响流体混合区以及尖钉和气泡的变形演化过程。

2011年，施红辉等［5］在大型水平激波管中，进行了液柱在激波及激波诱导的高速气流冲击下变形破碎的实验研究。该实验通过控制液柱初始直径，以及使用不同马赫数的激波，对液柱在冲击后从压缩变形到破碎雾化的过程进行了观察，比较了不同实验之间的差异；对液柱变形过程中的相关参数进行了测量分析，发现液柱迎风面出现RM不稳定现象。但在实验照片中，只能做到测量包括液柱初始直径、尖钉气泡大概尺寸、破碎雾化使用的大致时间等参数，不能得到具体的液柱变形过程的包括密度、速度、压强等物理特性的具体数据。本文在文献［5］液柱实验的基础上，根据该实验数据，以数值计算为手段，模拟整个液柱实验过程，利用计算软件得到实验过程中任意时刻液柱及其周围流场的压强、速度、密度等物理特性的数值，以进一步研究液柱实验中的RM不稳定性的影响。

1 二维和三维数学模型与计算方法

根据守恒关系，结合k-ε湍流模型和多相流VOF模型，液柱在激波冲击下RM不稳定性和破裂过程可由三维Navier-Stokes（NS）控制方程组表示。二维与三维控制方程组的区别在于三维方程组多了Z方向的量。三维的控制方程组可由下式表示：

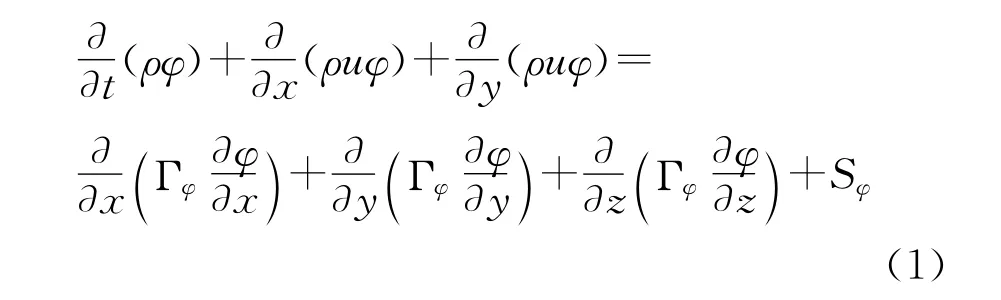
式中φ为通用因变量，Γφ为输运系数，Sφ为源项。对各方程而言，φ、Γφ、Sφ的具体含义见表1。

表1 三维控制方程的通用形式中各通用变量的含义

下面给出两组2D数值计算的模型。在第一组数值计算的数学模型中，选取2 cm×8 cm的计算区域，计算网格数设为168 040个。液柱在激波及波后高速气流冲击下的变形是非定常过程，本文对该过程进行了模拟，采用压力速度耦合的PISO算法，同时对密度、动量、能量方程中的对流项采用三阶MUSCL离散格式，对压力项采用Body Force Weighted离散格式，在VOF计算模型中，对体积分数则采用QUICK格式。具体计算模型如图1所示。

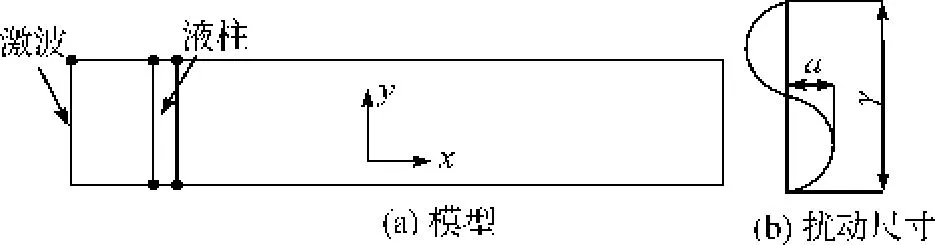
图1 2D计算区域示意

在2D数值计算中，如果柱体侧面轮廓是直线，那么可认为圆柱体表面是光滑的，高速气流会把液柱整体向右推动，液柱的外形保持稳定不变。因此，在后续的计算中，采用了带有初始扰动的边界模型，设置波长λ=0.05 cm，振幅a=0.01 cm，在液柱侧面一共有40个扰动波段，边界的扰动情况图1所示。

第二组模型同样选取计算区域为2 cm×8 cm，由于扰动振幅加大，计算网格数设为172 336个，设置波长λ=0.4 cm，振幅a=0.05 cm，在液柱侧面，共设置有5个扰动波段，计算参数设置与第一组相同。在第二组数值计算模型中，减少了液柱侧面上的扰动数目，相应的延长了扰动波长，并增大了扰动振幅。

使用Gambit软件进行网格划分，具体的三维模型如图2所示。

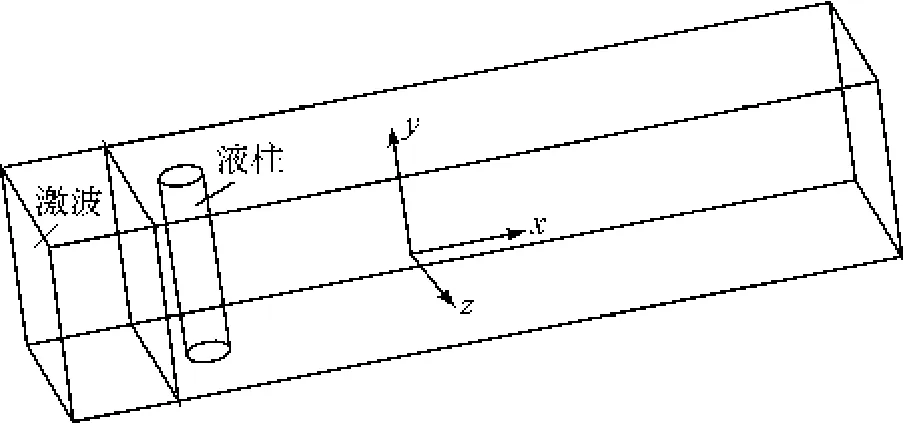
图2 计算区域三维模型

图2中，左侧区域表示高压区，圆柱体为液柱。因为要详细的观察液柱在激波冲击作用后的变形演化，所以这里需要对实验区域的网格进行细化。高压气体区域中的压力、密度、温度等物理特性数值设置高于右侧的低压气体，以使得在计算开始时，在这一物理特性间断面上，自然的形成向右传播的平面激波。同时设置高压气体的初始速度向右，尽可能的再现激波以及波后气流的运动状况。图2中，模型网格数量设为167 596个，计算时间步长设为5μs。数值模拟采用压力速度耦合的PISO算法，同时对密度、动量、能量中的对流项采用二阶迎风离散格式，对压力项采用Body Force Weighted离散格式，在VOF计算模型中，对体积分数则采用几何重构（Geo-Reconstruct）格式。

2 结果分析与讨论

当激波与波后气流对液柱产生作用时，液柱表面会的出现比较复杂的变化。根据文献［5］中的实验结果，随着时间的推移，可以观察到液柱迎风面出现典型RM不稳定性现象，出现尖钉和气泡。在下面给出的算例中，激波马赫数M=1.10、初始液柱直径为2.76 mm。

第一组2D的计算结果如图3所示。可以在图3中观测到，液柱的具体位移与文献［5］中的实验结果类似。从图3中不能明显看清楚微小液滴的剥离情况，但是可以看到液柱表面扰动随时间不断的增大，后期形成了RM不稳定性中典型的气泡和尖钉结构。但是，本文的数值计算结果与文献［5］中的实验结果有较大的不同。首先，从图3（4）开始可以看到液柱上下两端边角卷起形成了触角状。其次，从图3（8）开始，液柱靠近上下两端的位置出现中空结构，然而在实验中并没有发现类似现象。液柱的整体呈弓状结构，中间略窄，上下略粗。液柱迎风面出现扰动增大现象，背风面没有这一情况。实验中迎风面也发现了尖钉气泡结构，背风面由于液滴剥离形成了尾迹，在数值模拟结果中没有发现这一情况。最后，在图3（19）之后，尖钉状结构不再维持，开始上下摆动、融合、断裂。在实验中没有发现如此长度的尖钉结构，当尖钉和气泡结构发展到一定程度之后，它们会维持一定尺寸，最后随着整个液柱的裂解雾化一起崩碎。

图3 第一组2D液柱实验密度云图

图4 第二组2D液柱实验密度云图

第二组2D计算的结果如图4所示。对比实验结果，第一组数值计算结果整体液柱的变形速度与实验接近，尖钉等结构与实验结果更为吻合。第二组数值计算结果中，由于扰动数目降低，并且更为规则，因此引发的尖钉气泡结构较为规则，同时整体变形速度快于实验。两组数值计算结果的对比说明初始扰动的增加与扰动振幅的降低，会减缓整个液柱变形的速度。在实际过程中，尖钉结构不会拉伸过长，而是维持一定尺寸；在第二组数值计算结果中，出现尖钉结构拉伸过长的情况，主要原因是在计算中没有考虑Kelvin-Helmholtz（KH）不稳定性和湍流混合的影响的缘故。

图5为三维液柱的数值的计算结果，左侧为垂直沿轴线方向中央截面密度云图，右侧为水平沿轴线方向中央截面密度云图。从图5（a）图中可以看到，液柱的模拟结果中，液柱横向移动速度不断变大，其表面有微小液滴剥落，最后发生液柱断裂现象。图5（b）表明，液柱横截面形状是沿激波管径向的直径增大，沿激波管轴向的直径降低，呈扁平化发展，微小液滴从液柱表面不断剥离，最后发生崩溃、破碎。对比文献［5］，整个液柱的失稳及破裂过程的模拟结果与实验结果吻合较好。特别地，数值计算提供了液柱核心破裂的过程：从图5b（6）-b（7）中可以看到，液柱从横截面方向上出现破裂，并且轴向也出现断裂；文献［5］中的实验照片中，只能观察到重叠在一起的影像，而不能分辨出液柱变形的细节，无法判断液柱是否断裂。

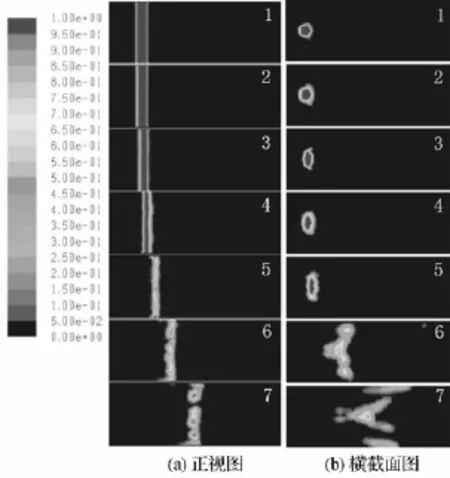
图5 三维液柱实验数值计算结果

图6是液柱中部在（X，Z）平面里，即在横向截面上的静压云图。其中，图6（1）-（3）中，液柱尾部上下各形成了一对称的低压区域。该区域随时间增大，有一定的对称性。对比密度图，液柱Z方向直径逐渐增大，其前方形成一块较规则的高压区域。图6（5）开始，液柱后方的压力分布开始出现明显的不均匀。图6（6）-（7）中，液柱从轴向和横截面方向上开始破碎断裂，流场变得非常紊乱。

图6 液柱横向截面上的静压云图变化过程

图7是模型部（X，Z）平面上的速度云图。图7（1）-（4）中，中间面积较大的一块零速度区域，即深蓝色区域，其形状与密度云图中的液柱横向截面的形状完全吻合。液柱左右两侧的高速区域不断扩大，并且速度不断上升，最高速度达268 m/s，此时，液柱表面存在气体与剥离的微小水滴的混合流。同时液柱横向截面尾部后方形成了低速区域扩张而形成的火焰状尾翼。图7（5）开始，液柱横向截面的火焰状尾翼摆动明显，速度场越来越不稳定。从图7（6）-（7）可以看出，液柱周边的速度场已经极度紊乱，此时，可以看到液柱在横截面方向上已经破裂。

图7 液柱横向截面上的速度云图变化过程

利用三维计算结果，可以从横向和纵向两个方向来观察液柱变形断裂过程中的细节。可以看出，液柱首先在横截面方向上发生破裂，随后在轴向上也发生断裂。对比实验结果，在三维数值计算结果中，液柱横向位移发生的更快，整体变形破裂的速度也要更快；并且在液柱后方没有出现实验中的大规模微小液滴的剥离、雾化。产生这种现象的原因可能是：第一，计算模型中参数的设定不能完全符合实验环境，以及Fluent软件本身存在局限性，导致计算结果与实验过程存在偏差；第二，液滴剥离时与空气混合，其密度接近空气，因此在计算结果图中难以分辨。

3 结 论

本文利用非定常的二维和三维Navier-Stokes（NS）方程、标准k-ε湍流模型和多相流VOF模型，对液柱在激波诱导的高速气流中的变形断裂现象进行了数值计算与分析，得到如下结论。

a）二维（2D）液柱数值计算模拟中，由于加入了初始扰动，出现了尖钉与气泡状结构，即出现了RM不稳定性。在第一组数值计算中，由于扰动数目较多，扰动的振幅较小，得到的数值计算结果中，液柱整体变形速度与实验结果接近。

b）三维（3D）液柱数值计算中，虽然液柱表面并没有初始扰动，但由于在垂直于液柱方向上，液柱存在初始边界形状，因此在高速气流的作用下仍然会出现RM不稳定性的特征。在时长1.75 ms的数值模拟过程中，液柱完成了变形断裂过程，但在实验中，这一过程历时4 ms左右，因此数值计算结果中液柱的变形速度要快过实验。从具体的演变过程可以得出结论，由于液柱在横截面平面（Z方向）发生变形失稳，导致沿液柱轴向随之出现变形失稳。

c）二维计算接近实验结果，但三维计算更符合实验结果，在进行数值研究时，更应采用三维计算方法。在本文二维（2D）数值计算过程中，存在Fluent软件系统将液柱辨识为“液墙”的问题；三维（3D）计算存在RM不稳定性现象不明显，即没有出现文献［5］中实验照片上的尖钉气泡状结构，以及数值计算中液柱变形断裂速度存在过快的问题。

在后续研究中，为了提高数值计算的可靠性，需要进一步对计算模型进行优化设计，并对Fluent软件在该算例中的相关参数设置做进一步的优化调整，以得到更加真实可信的数值计算结果。

［1］Igra D，Takayama A.Investigation of aerodynamic breakup of a cylindrical water droplet［J］.Atomization and Sprays，2001，11（2）：167-185.

［2］柏劲松，李 平，陈森华，等.内爆加载下果冻内外界面不稳定性数值计算［J］.高压物理学报，2004，18（4）：295-301.

［3］Chen H，Liang S M.Flow visualization of shock/water column interactions［J］.Shock Waves，2008，17（5）：309-321.

［4］王 涛，柏劲松，李 平.二维气/液界面不稳定性数值模拟［J］.高压物理学报，2008，22（3）：298-304.

［5］施红辉，吴 宇，肖 毅，等.激波与液柱相互作用时的气动特性研究［C］//中国力学学会流体力学专业委员会实验流体力学专业组.第9届全国实验流体力学学术会议论文集，2013：36-42.

NumericaI CaIcuIation of RM InstabiIity and Rupture Process of Liquid CoIumn under Impact of Shock Waves

WU Yu，SHI Hong-hui，WANG Chao，YE Bin，ZHANG Ke
（School of Mechanical Engineering&Automation，Zhejiang Sci-Tech University，Hangzhou 310018，China）

This paper calculated the deformation and rupture process of the liquid column under the impact of shock waves and studied specific representations of Richtmyer-Meshkov（RM）instability in the process.Fluent software is used to carry out numerical simulation of evolutionary process of RM instability on gas/liquid interface and flow field around the gas of 2D and 3D liquid columns when shock mach number is 1.10 and initial diameter of shock mach number is 2.76 mm.The results show that the number of initial perturbation imposes significant influences on RM instability；the liquid column deforms and loses stability along the cross section（direction Z），so deformation and instability appear along axial direction of the liquid column.The numerical calculation results well coincide with experimental results.

RM instability；shock wave；liquid column；numerical calculation

O354.5；O359

A

（责任编辑：康 锋）

1673-3851（2014）05-0502-05

2014-03-03

吴 宇（1983-），男，江西玉山人，硕士研究生，研究方向为湍流与复杂流动以及可压缩性与瞬态流动。

施红辉，E-mail：hhshi@zstu.edu.cn