求解不等式约束极大极小值问题的罚函数方法

郑芳英

（浙江理工大学理学院，杭州310018）

求解不等式约束极大极小值问题的罚函数方法

郑芳英

（浙江理工大学理学院，杭州310018）

构造一个新的简单精确光滑罚函数来求解含不等式约束极大极小值问题。首先通过添加一个变量，将含不等式约束的极大极小值问题转化为与之等价的连续约束优化问题，然后利用新的简单精确光滑罚函数，对等价的连续约束优化问题进行求解。在扩展的MF约束规范条件下，可以证明：当罚参数充分大时，无约束优化问题的局部极小点也是原极大极小值问题的局部极小点。算例结果表明，给出的罚函数方法可有效地求解含不等式约束的极大极小值问题。

约束优化问题；无约束优化问题；罚函数方法；极大极小值问题

0 引 言

极大极小值问题是优化问题的重要分支，工程优化设计、电子线路优化设计、经济管理等许多实际问题都可以建模为极大极小值问题。本文研究如下含不等式约束的极大极小值问题：

其中fi：Rn→R（i=1，…，q），gi：Rn→R（i=q+1，…，m）为连续可微函数。

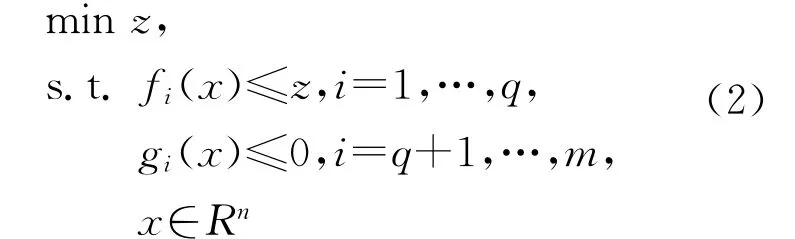
其中z∈R是新引进的变量。显然问题（1）与问题（2）是等价的，从而可以利用已有的求解连续非线性规划的算法求解问题（1）。

罚函数方法是求解连续约束优化问题的一种重要方法，其思想是将约束优化问题转化为无约束或仅含简单约束的优化问题来求解。但是传统的罚函数要么简单精确，但不是光滑的，如l1精确罚函数；要么光滑，但不是精确的，如二次罚函数；要么光滑精确的，但不是简单的。这里的“简单”是指罚函数中仅含目标函数及约束函数，而不含其梯度的信息。

2003年，Huyer等［4］通过增加一个变量，针对下式约束优化问题（3）给出了一个新的简单精确罚函数。

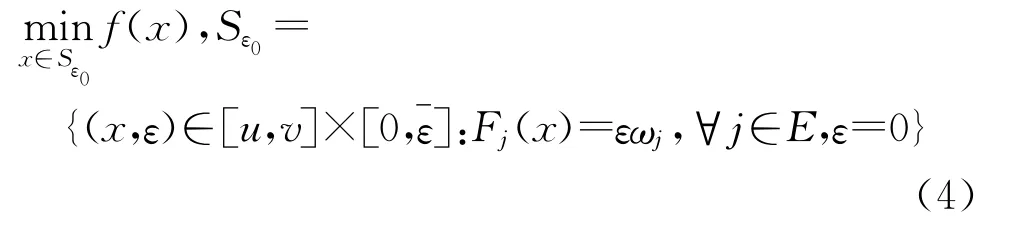
其中［u，v］=｛x∈Rn：u≤x≤v｝为Rn中具有非空内部的箱子约束，f：D→R，Fj：D→R（∀j∈E）连续可微函数，而D为含［u，v］的开集。固定ωj（∀j∈E），考虑如下等价问题：

相应的罚问题为：

在一些常规的假设下，文献［4］证明了罚问题（5）的局部极小点正好也是原问题（3）的局部极小点；同时证明，对于问题（5），当ε＞0时，对于充分大的σ，问题（5）不存在KKT点，而通常算法得到的点是KKT点。

Di Pillo等［5］考虑了无约束的极大极小值问题，首先将极大极小值问题转化为一般连续约束优化问题，然后对转化后的约束优化问题利用可微的罚函数方法进行求解；Ma等［6］借用了文献［5］的方法，考虑了带等式约束的极大极小值问题，利用一个新罚函数方法对转化后的约束优化问题进行求解。

受到文献［5-6］的启发，本文在文献［6］的研究基础上，考虑含不等式约束的极大极小值问题，提出基于简单精确光滑罚函数方法的求解问题（1）的一个新算法。

1 简单精确光滑罚函数

定义集合：T=｛（x，z）∈Rn+1：fi（x）-z≤0，∀i=1，…，q；gi（x）≤0，i=q+1，…，m｝，则问题（2）可以等价为下列优化问题：

其中ωi∈（0，1）（i=1，…，m）。类似地，定义集合Tε：

Tε=｛（x，z，ε）∈Rn+2：fi（x）-z≤εγωi，∀i=1，…，q；gi（x）≤εγωi，i=q+1，…，m｝。

对于问题（6），定义罚函数如下：

其中α、β、γ、δ都是偶的正整数，且

相应的罚问题为：

下面来讨论罚函数fσ（x，z，ε）的可微性和精确性。

定理1设（x，z）→（x*，z*）∈T，ε→ε*=0，且γ＞δ＞α＞0，2δ-α＞0，β＞1，

则有：lim fσ（x，z，ε）=fσ（x*，z*，0）=z*，

证明 当ε≠0，0＜1-cε-2δΔ（x，z，ε）＜1时，有0＜ε-2δΔ（x，z，ε）＜c1，即0＜Δ（x，z，ε）＜c1ε2δ，从

而有Δ（x，z，ε）=O（ε2δ），可得：

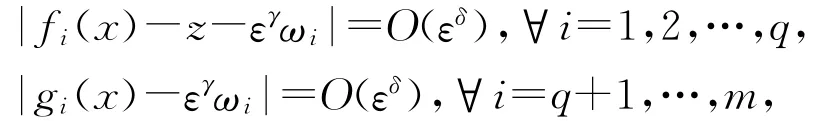
即

故

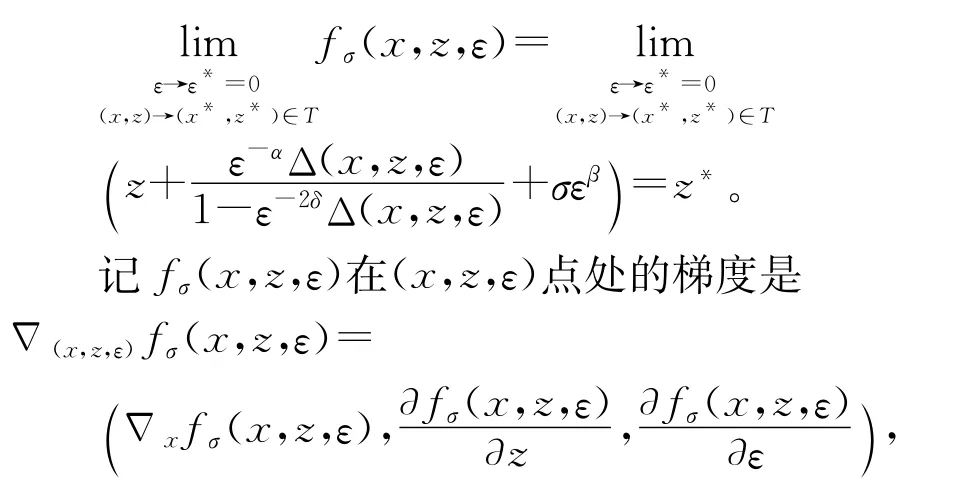
其中，

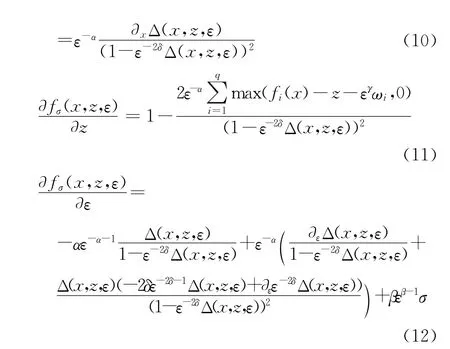
将Δ（x，z，ε）表达式代入式（10-12）以及由关系式（9），可得：

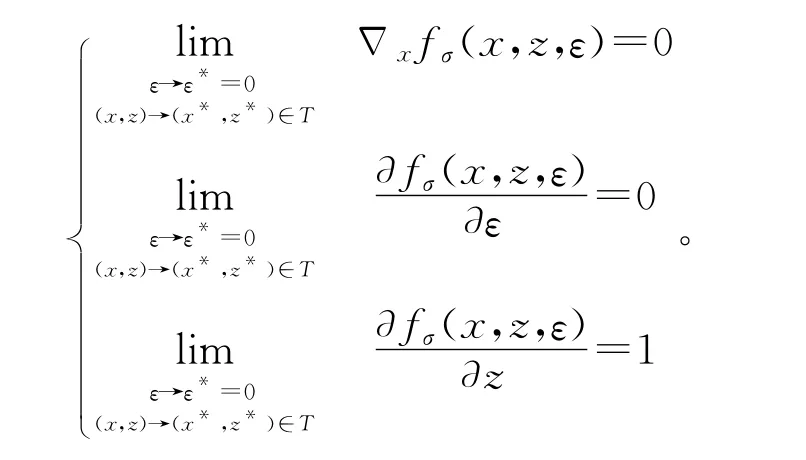
从而，罚函数fσ（x，z，ε）在Rn+2上是连续可微的。

引理1 在目标函数fσk（xk，zk，εk）为有限值且εk≠0条件下，如果（xk，zk，εk）∈L（Pσk），则（xk，zk，εk）∉Tεk。其中L（Pσk）表示罚问题（Pσ）的局部极小点。

证明目标函数fσk（xk，zk，εk）为有限值且εk≠0，（xk，zk，εk）∈L（Pσk），所以，可以得到：

若（xk，zk，εk）∈Tεk，则βεβ-1σk≠0，矛盾。所以（xk，zk，εk）∉Tεk。

定理2如果（xk，zk，εk）∈L（Pσk），在目标函数fσk（xk，zk，εk）为有限值，且εk≠0时，设（xk，zk，εk）（x*，z*，ε*）（x*）（i=q+1，…，m）在x*处满足EMFCQ条件，则ε*=0，（x*，z*）∈T。

证明由εk≠0，（xk，zk，εk）∈L（Pσk）及关系式（10-12），可以得到：

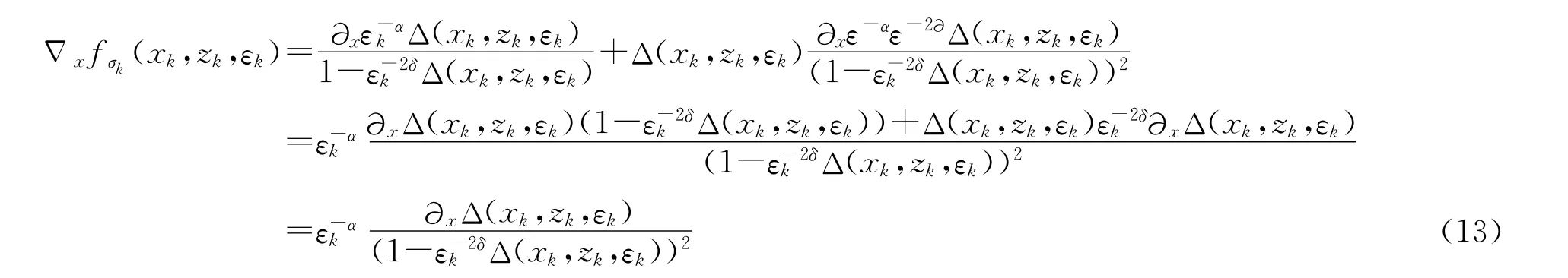
由式（15），可以得到：

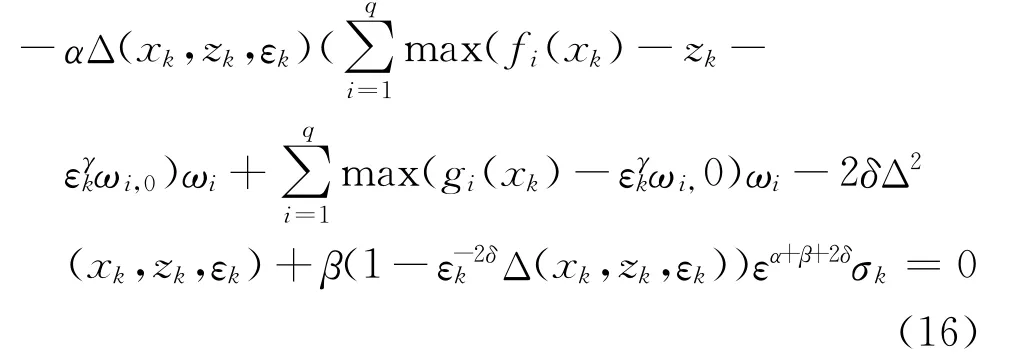
在式（16）两端，令k→+∞，则式子的前三项都是有限值，而且

又由式（14）可以得到：

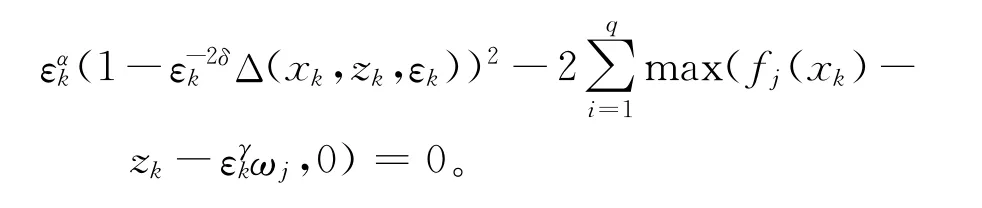
从而可得：

fi（x*）-z*-（ε*）γωi≤0，i=1，…，q，即fi（x*）-z*≤（ε*）γωi，∀i=1，2，…，q。

由式（13）可得：

在x*处，定义如下指标集：

I0（x*）=｛i∈I：gi（x*）=0｝，

I+（x*）=｛i∈I：gi（x*）≥0｝，

I-（x*）=｛i∈I：gi（x*）＜0｝，

其中，I=｛i｜i=q+1，…，m｝。

由假设Δgi（x*）在x*处是满足EMFCQ条件，即在x*处，∃p∈Rn，使得：Δ

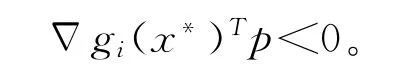
假设I+（x*）I0（x*）≠Ø，则至少存在某个i∈I+（x*）I0（x*），使得

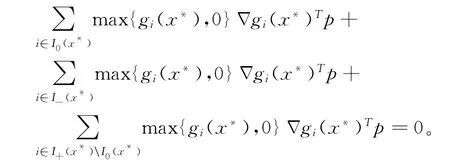
所以有：

矛盾。所以I+（x*）I0（x*）=Ø，即I+（x*）=I0（x*）。而I=I+（x*）∪I0（x*）∪I-（x*）。所以gi（x*）≤0，i∈I。因此，

即（x*，z*）∈T0。

定理3如果（xk，zk，εk）∈L（Pσk），在目标函数fσk（xk，zk，εk）为有限值且εk≠0时，α、β、γ、δ满足-α-β+2δ≥0，-α-β+δ+γ≥0，那么存在k0＞0，当k≥k0时，εk=0，（xk，zk）∈L（P）。

证明假设这个定理是不成立的。设存在一个子列｛（xnk，znk，εnk）｝⊆｛（xk，zk，εk）｝，对于任意的k0＞0k0＞0，当nk≥k0，εnk≠0时，由目标函数fσnk（xnk，znk，εnk）为有限值且εnk≠0，由引理1，有（xnk，znk，εnk）∉Tεn，因此，由式（15）可得：

k

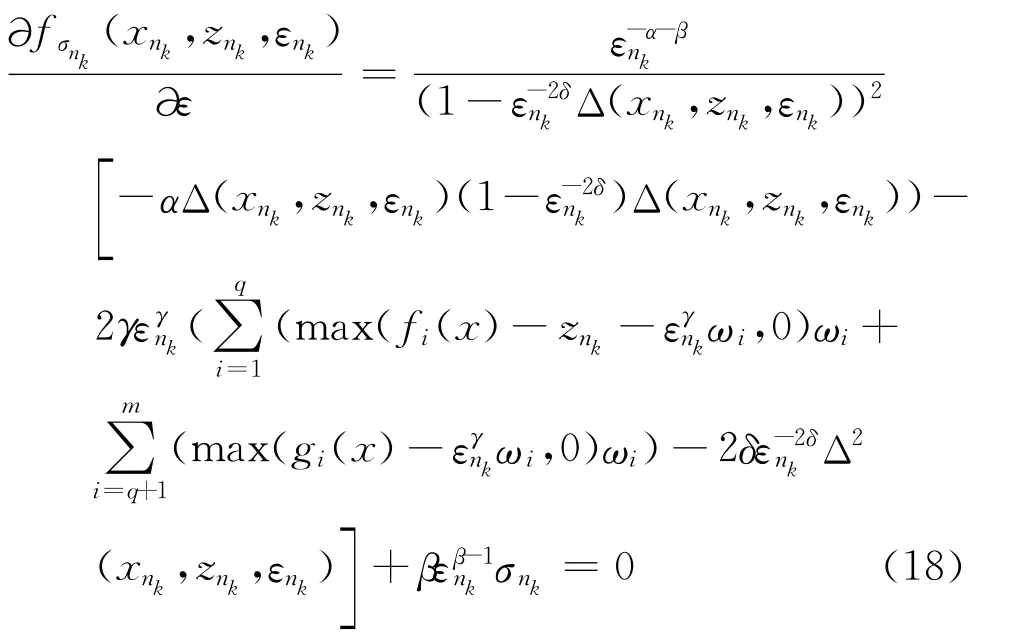
由定理2，有：εnk→ε*=0，（xnk，znk）→（x*，θ*）∈T。又由εnk≠0，0＜1-cεn-2δkΔ（xnk，znk，εnk）＜1，可以得到：

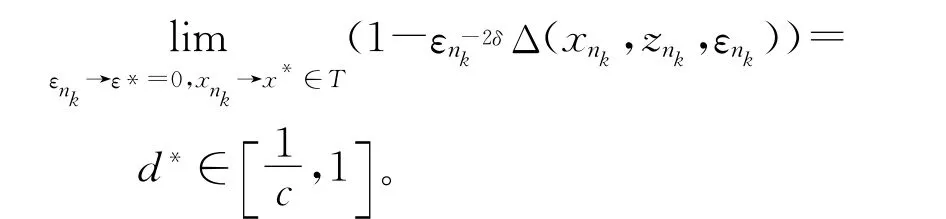
由题设：-α-β+2δ≥0，-α-β+δ+γ≥0，式（18）左边不可能等于0，矛盾。因此，不可能存在这样子列。所以，存在k0＞0，当k≥k0时，有：εk=0，（xk，zk，0）∈L（Pσk），此时xk和zk满足：

因此，由（xk，zk，0）∈L（Pσk）知，存在点（xk，zk，0）某个邻域U，对任意（x，z，0）∈U∩（T×｛0｝），有：zk=fσk（xk，zk，0）≤fσk（x，z，0）=z。所以，（xk，zk）∈L（P）。

在这部分，针对问题（2）给出了一个新的简单精确光滑罚函数，通过证明，当罚参数σ足够大时，罚问题的局部极小点也是原问题的局部极小点。

2 数值算例

为了验证本文提出方法的有效性，下面给出两个数值算例，且算例在Matlab 7.5.0编程环境下运行。

算例1［7］

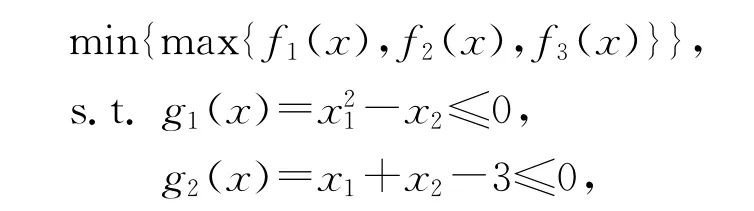
其中f1（x）=+，f2（x）=（2-x1）2+（2-x2）2，f3（x）=2exp（-x1+x2）。在文献［7］中，初始点设为x（0）=（0，0），最优解为x*=（1，1），对应最优目标函数值为2。利用本文提出的罚函数方法，取参数值分别为：α=2，β=6，δ=4，γ=6，ω=0.05，初始点为x（0）=（0，0），ε0=3，得到如表1数值结果。

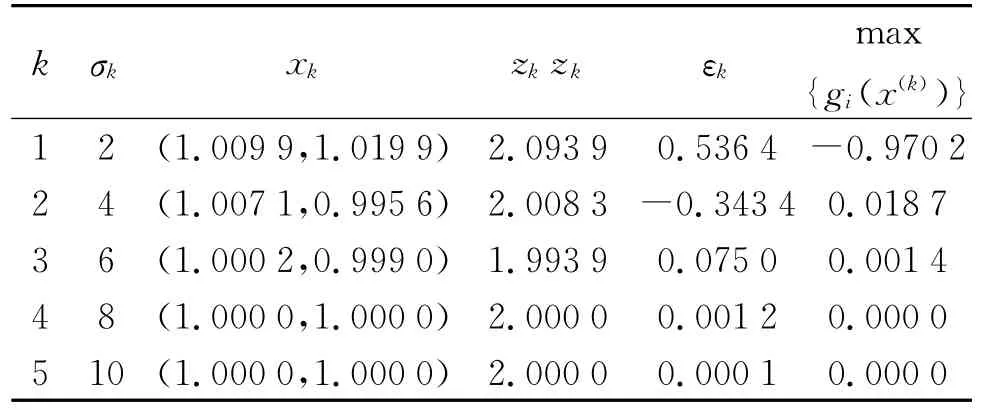
表1 算例1的数值结果

算例2［7］

其中，f1（x）=（x1-2）2+（x2-1）2，f2（x）=（3x1+ x2-4）2。在文献［7］中，取初始点为x（0）=（2，2），最优解x*=（1，1），最优目标函数值为1。利用本文提出的罚函数方法，取参数值分别为：α=2，β=6，δ=4，γ=6，ω=0.05，初始点为：x（0）=（2，2），ε0=2。

算例的数值结果见表2。

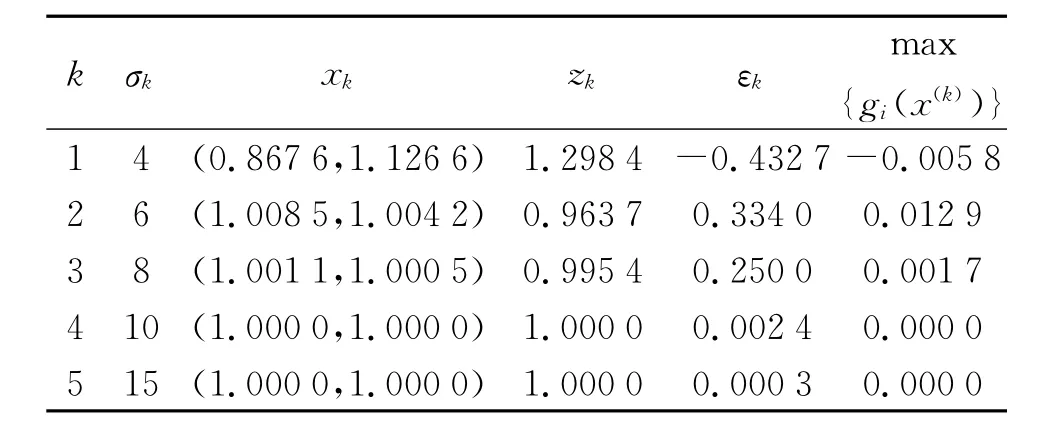
表2 算例2的数值结果

从以上两个算例可以看到，通过适当的选取相关参数，当罚参数σ取的不是很大时，就可以得到原问题的最优解，从而说明本文给出的罚函数方法对于求解含约束的极大极小值问题是可行的。

3 结 论

本文在理论上给出了求解极大极小值问题的罚函数方法，并证明了该方法的可行性。文中给出的罚函数不同于传统的罚函数，同时具有光滑性和精确性，而且不论原问题约束函数有多少个，罚问题与原问题比较，其变量仅增加了一维。因此，对于目标函数和约束函数都是连续的极大极小值问题，本文提供了光滑化的求解途径。

本方法由于罚函数中用到的参数比较多，在算法设计时需要不断地对参数进行调整，影响算法的效率。在之后的研究中，将考虑构造参数较少的精确光滑罚函数。

［1］Polak E，Mayne D H，Higgins J E.Superlinearly convergent algorithm for min-max problems［J］.Journal of Optimization Theory and Applications，1991，69（3）：407-439.

［2］Gaudioso M，Monaco M F.A buddle type approach to the unconstrained minimization of convex nonsmooth functions［J］.Mathmatical Programming，1982，23（1）：216-226.

［3］李兴斯.解非线性极大极小值问题的凝聚函数法［J］.计算结构力学及其应用，1991，8（1）：86-92.

［4］Huyer W，Neumaier A.A new exact penalty function［J］.SIAM Journal of Optimization.2003，13（4）：1141-1158.

［5］Di Pillo G，Grippo L，Lucidi S.A smooth method for the finite minimax problem［J］.Mathematical Programming，1993，60：187-214.

［6］Ma C，Li X，Cedric Yiu K F，et al.New exact penalty function for solving constrained finite min-max problems［J］.Applied Mathematics and Mechanics，2012，33（2）：253-270.

［7］唐焕文，张立卫，王雪华.一类约束不可微优化问题的极大熵方法［J］.计算数学，1993，15（3）：268-275.

PenaIty Function Method for SoIving Finite Min-Max ProbIem IncIuding InequaIity Constraints

ZHENG Fang-ying
（School of Sciences，Zhejiang Sci-Tech University，Hangzhou 310018，China）

A new simple exact and smooth penalty function is constructed to solve min-max problem of inequality constraints.Firstly，through adding a variable，min-max problem including inequality constraints is transformed to equivalent continuous constraint optimization problem.Then，equivalent continuous constraint optimization problem is solved with new simple exact and smooth penalty function.Under extended-MF constraint standard conditions，it is proved that when the penalty parameter is sufficiently large，local minimum point of unconstrained optimization problem is also local minimum point of the original min-max problem.The calculation results show this penalty function method is an effective approach for solving min-max problem including inequality constraints.

constraint optimization problem；unconstrained optimization problem；penalty function method；min-max problem

O221.2

A

（责任编辑：康 锋）

1673-3851（2014）05-0559-06

2014-03-31

国家自然科学基金（51075421）；浙江理工大学科研启动基金（1206830-Y）

郑芳英（1979-），女，浙江衢州人，博士，讲师，主要从事非线性最优化理论研究。