基于三维扫描点云对渐开线斜齿圆柱齿轮的参数提取
王春香,石宏民
(内蒙古科技大学机械工程学院,内蒙古包头014010)
0 前言
齿轮的测绘和参数反求工作技术性很强,对测绘人员的齿轮设计、加工和检验经验要求高。致使本地区的一些厂矿企业存在由于缺少对于齿轮参数提取方法研究的专业技术人员,在遇到有齿轮产品实物,而无原始设计图纸的情况下,难以快速、准确地反求出齿轮基本参数和其主要几何尺寸的问题。为了解决现场存在的类似问题,以来源于某现场的尚未使用的渐开线圆柱斜齿轮产品为对象,基于实物逆向工程技术,研究了其基本参数和主要几何尺寸的反求方法。目前,关于变位渐开线圆柱直齿轮基本参数的提取方法已经有一定的研究成果[1-2]:文献[1]基于较高精度量具采用传统的测绘法和啮合理论,结合汽车行业标准,反求了进口启动机驱动用高度变位圆柱渐开线直齿轮的参数。文献[2]以三坐标机在任意端面测得的少量齿廓线离散测点为依据,通过以三次多项式近似齿廓渐开线及利用测点的齿形误差的方法拟合出基圆半径,再以基圆推算模数,进而利用模数、压力角的组合可能试算模数和压力角的方法借助计算机编程实现了反求一配对的高度变位直齿圆柱齿轮的参数;并给出了一种实用的“基圆拟合算法”。前者是在齿轮的产出国、行业及用途背景及齿廓线线型已知为渐开线的前提下,易受到人为测量操作以及经验的影响,而可能使齿轮参数提取的一次精确度不高,后者没有充分利用数字化检测的准确、高效和便捷性,以及基圆半径的拟合及反求计算需要进行底层编程,使反求过程显得较为复杂、效率不高。本文作者借鉴了文献[2]中初始基圆半径的修正方法,以能否反求出基圆半径来判定齿轮的齿廓线是否为渐开线(不同之处在于初始基圆半径的选取原则,且文献[2]中为了用三次多项式拟合曲线,通过坐标转换到局部坐标系,进行了大量的底层编程,而本文运用曲线拟合工具箱,可以直接完成曲线拟合工作);结合文献[2]的反求思路,充分利用数字化测量手段,并借助Matlab 语言及其曲线拟合工具箱,可以较为准确、高效地提取一配对渐开线斜齿轮的参数。
1 反求步骤
1.1 反求思路
首先,依据轮齿点云确认齿廓线为渐开线,在此基础上,建立齿轮的端面齿形,利用PRO/E 软件的测量功能,测量齿形相关的主要几何尺寸(齿顶圆直径、齿根圆直径、齿全高、公法线长度等),进而反求出基本参数(模数、压力角、齿顶高系数、顶隙系数、螺旋角等)。
1.2 点云数据处理
点云是建立端面齿形和判断廓线的重要依据,所以将Imageware 中的系统误差有效数值设定为精确到小数点后第四位,将齿轮点云的中心轴取定为z轴,精确取定方法是,利用齿轮的两端轴点云分别拟合圆柱,取圆柱轴心线,再将二者轴心拟合为同一轴线,将此轴线与z轴对齐,取与z轴垂直的截面从齿宽部位(即轮齿的上端面和下端面之间)的上、中、下三部分截取齿轮点云;判断齿廓线类型时,考虑到齿轮齿形多是渐开线以及齿轮修形的问题,为保证齿形特征正确,选取点云时,视总点数而定,需去除掉占齿全高点云约1/10 的根部点云。
依据点云建立齿轮的端面齿形时,点云的处理原则是:齿顶圆处3 点以上,齿根圆角处3 点以上,廓线点4 点以上,运用圆弧拟合齿顶圆以及齿根圆角,使用依公差构造曲线命令拟合齿廓线(* .imw),分别将各轮齿保存为IGS 格式,运用PROE 软件打开文件,在草绘命令中已经默认齿轮中心为坐标原点,以原点为中心,作圆分别与齿顶圆弧、齿根圆弧相切,其直径即为测量得到的齿顶圆直径、齿根圆直径,由于草绘中没有阵列命令,只能根据齿轮齿数计算轮齿间的角度,作复制旋转,进一步测量公法线长度。
1.3 判定齿廓为渐开线的方法
第一步:初始基圆半径的确定
假设反求齿轮为渐开线齿轮,渐开线上任意点的法线与基圆相切,且齿轮中心到法线的垂直距离为基圆半径,则确定初始基圆半径需要在齿廓上选取一个基准点,根据测点个数为奇、偶数的不同确定基圆半径时,基准点的选取方法也不相同。
若为奇数时,如图1所示,连接中间点两旁的点A和点B,AB所在直线为m,过AB中点作直线m的垂线n,n与测点拟合曲线交于点O1(即为拟合初始基圆半径的基准点);若为偶数时,取中间两点A和B,其他作法同上。其中n即为拟合渐开线的法线,取坐标原点O到n的距离为初始基圆半径。

图1 初始基圆半径
第二步:初始渐开线的生成
通过初始基圆半径按渐开线形成原理生成初始渐开线(第一个新生渐开线),与测点拟合曲线建立了误差分析依据。
第三步:根据齿形误差(Δ,见图2所示)修正基圆
如图2所示,新生渐开线O1P0与测点拟合曲线O1P交于点O1,点P为点O1附近的一测点,过点P作初始基圆的切线PB,交曲线O1P0于点P0,设虚线与的夹角为调整角Δθ,线段为齿形误差Δ,由于Δ ≅Δθ·,则以O1为基点,将曲线O1P0向曲线O1P旋转Δθ,同时调整法线,取原点O到法线的距离为新生基圆半径,以此半径再次生成了渐开线,重复以上步骤,直至调整角Δθ 和齿形误差Δ 趋近于零,且小于给定误差ε=10-q,根据多次实验发现,当q值大于4 以后,迭代较为稳定;当q值大于12 以后,迭代结果非常理想。
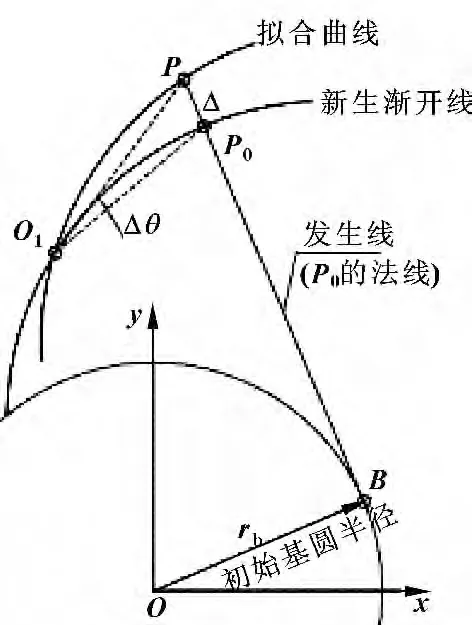
图2 误差原理
第四步:齿形分析
按以上原理,依据齿廓线测点坐标数据,运用Matlab 软件的曲线拟合工具箱和图形功能,若可以得出较为稳定的基圆半径值,且调整角和齿形误差极为接近0 值,则可判定齿廓为渐开线性质;否则,不是渐开线。
1.4 几何尺寸的测量和基本参数的反求
判定了齿轮类型之后,则可以明确其基本参数包括:齿数、模数、压力角、齿顶高系数、顶隙系数、螺旋角、变位系数;利用proe 中的数字化测量功能,需要测量的主要几何尺寸包括:齿顶圆直径、齿根圆直径、齿全高、公法线长度等。设定精确到小数点后第二位,取平均值为最终数值。公法线长度的跨测齿数由经验公式(k=z/9 +0.5)初定,测量得出的齿全高根据齿轮齿高(表1),可以查出齿顶高系数与顶隙系数c*,基圆齿距可以根据公法线长度求得,公式如下:pb=Wn+1-Wn,并基于基圆齿距(表2)得出对应的模数和压力角。

表1 部分齿轮齿高表[3]

表2 部分基圆齿距(基节)数据表[3]
1.5 变位的反求
表3 为文献[4](机械设计手册)中斜齿轮的公法线长度计算公式,从计算公式中可以看出,公法线长度与变位系数是密不可分的,根据表6 计算出标准斜齿轮的公法线长度W,并求出公法线长度的上、下偏差Ewms和Ewmi[4];测得公法线的实际长度W',如果W'落在偏差范围内,则说明齿轮符合标准齿轮的切制要求;若W'落在偏差范围外,则齿轮为变位齿轮。
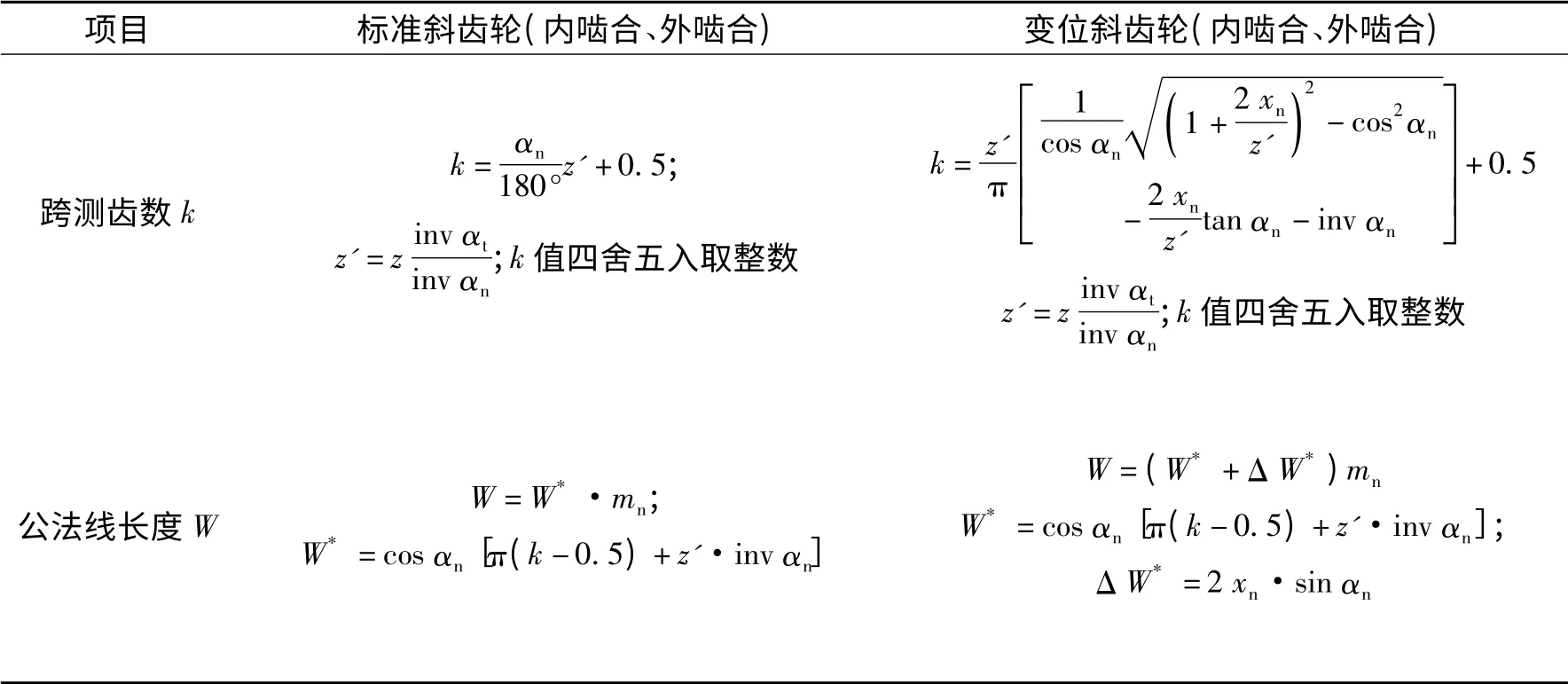
表3 公法线长度计算公式[4]
2 反求实例
如图3(a)所示,通过实物照片可直观判断这对齿轮为外啮合斜齿圆柱齿轮,齿数z1=24,z2=27;图3(b)是在Imageware 软件中读取的齿轮点云模型。

图3 齿轮实物及其点云
2.1 点云数据处理
将齿轮轴心取定为z轴的效果如图4所示,根据每个截面齿廓线点云完整性(即点云数量较多且分布均匀)的不同,3 个截面选取的轮齿个数分别为:4 个、5 个、4 个,且选取同一轮齿的双侧廓线点云作为研究对象。图5 是Matlab 中读取的部分廓线坐标点数据,考虑到找O1点的规则不同以及测点处理方法的可行性,需要选取同一轮齿两侧齿廓的测点,且测点个数要存在奇数和偶数。

图4 点云对齐效果

图5 小齿轮齿面测点数据
部分轮齿的齿形拟合效果如图6所示。

图6 拟合后的齿形
2.2 判定齿廓线是否为渐开线
设定误差ε=10-12,图7(a)中的基圆半径值稳定在64.35 mm,图7(b)中调整角趋近于零值,则说明齿轮的齿廓线符合渐开线的生成原理,则这对齿轮为渐开线斜齿圆柱齿轮。

图7 基圆半径反求
表4 为小齿轮截面2 中5 个轮齿的基圆半径拟合结果,同理,可求出大齿轮的基圆半径值,则对二者的基圆半径取平均值如下:
小齿轮基圆半径rb1=56.859 mm大齿轮基圆半径rb2=64.789 mm

表4 小齿轮基圆半径反求 mm
2.3 端面模型的测量以及参数的反求
既然判定了齿轮为渐开线斜齿圆柱齿轮,图8 中即为部分测量的齿顶圆与齿根圆直径尺寸,设定精确到小数点后第四位,取平均值为最终数值。
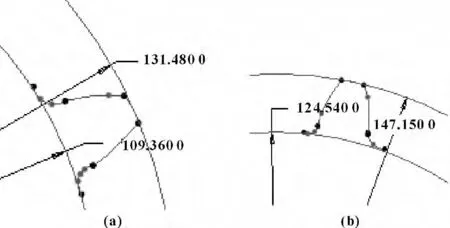
图8 几何尺寸的测量
根据公式计算跨齿数:小齿轮k=3;大齿轮k=4。
端面模型测量的主要几何尺寸数据取平均值如表5所示。

表5 主要几何尺寸测量数据
在齿轮齿高表1 中,齿全高接近11.25,则取齿全高为h=11.25,对应的模数mn=5、齿顶高系数、顶隙系数。
计算得出基圆齿距数据如表6所示。

表6 基圆齿距值计算
则由基圆齿距表2 可知模数mn=5、压力角αn=20°。
2.4 变位的反求
根据文献[5]中公法线上、下偏差的计算方法以及实例的应用,总结了6—8 级公法线长度上、下偏差值,如表7所示。

表7 公法线的上、下偏差
根据齿轮的齿形特征、使用环境、粗糙度等判断齿轮的精度等级大约为6 级,则选取公法线长度的上、下偏差分别为-0.144 和-0.198。
根据公式计算出标准斜齿圆柱齿轮的跨齿数、中间变量(W'、z')、公法线长度以及上、下偏差,还有实际测量的公法线长度值,如表8所示,则判定齿轮为标准渐开线斜齿圆柱齿轮。

表8 小齿轮的变位判定
2.5 螺旋角的反求
表3 中,代入中间变量后,变位斜齿轮的公法线长度Wk的计算公式如下:
Wk=mncos αn[π(k-0.5)+ z'·inv αn+2xn·tan αn]
于是推导出端面压力角αt

则可求出螺旋角

为了验证齿轮参数反求方法的可行性,将反求参数与已知的齿轮设计参数进行对比分析,表9 为反求参数与理论参数的比较,表10 为反求几何尺寸与理论几何尺寸的比较。

表9 反求参数与理论参数的比较

表10 反求几何尺寸与理论几何尺寸的比较
齿轮原始设计参数中取6 级精度,在高精度的齿轮机床上范成加工,齿面最终精加工需要精密磨齿或剃齿,齿面粗糙度1.6,齿根粗糙度3.2,用于在高速下平稳地回转,并要求有最高的效率和低噪声的齿轮。根据表9 和表10 的结果验证可知,所求参数基本控制在不影响齿轮实际应用的前提下,符合齿轮实际测量要求。
3 结论
基于实物逆向工程技术、齿轮实际测绘理论、数值分析理论等深入地研究了渐开线斜齿圆柱齿轮的参数提取途径,在借鉴文献[2]中基圆半径反求算法的基础上,进行了简化,并综合利用了Matlab 语言及其工具箱、三维CAD/CAM 软件系统PRO/E 和Imageware 逆向软件系统,实现了斜齿轮的齿形定性和主要几何参数反求。和已有的方法相比,即无需使用实物高精度量具、又避开了利用高级语言进行底层编程的复杂劳动,在几何尺寸计算时采用计算机编程,可以实现自动、高精度、重复计算;相对而言具有较高的效率、易用性及可操作性,并减少了人为主观判断因素的影响。
反求结果和实际设计参数之间的误差的产生和所测点云的质量、测量点云时喷涂的显像剂的厚度不均、齿轮自身的制造误差以及反求处理方法相关;反求过程中如何全面考虑、分析以上因素等对结果的影响以完善反求方法,使得反求结果的准确性、稳定性更为理想、便于工程实际中应用的问题有待进一步的研究。
[1]周彭.进口启动机驱动齿轮的测绘及计算[J].汽车电器,1994(6):13-19.
[2]陈丽萍,帅梅,杨川,等.一种反求渐开线齿轮(或花键)参数的实用方法[J].机械科学与技术,2001,20(3):353-355,358.
[3]张展.齿轮设计与实用数据速查[M].北京:机械工业出版社,2009.
[4]成大先.机械设计手册·第3 卷[M].5 版.北京:化学工业出版社,2008.
[5]茆燕荷.摩托车最理想的齿轮齿厚减薄量[J].摩托车技术,1995(2):3-5.
[6]赵振江.逆向法选择渐开线齿轮的变位系数[J].机械传动,2008,32(4):48-59.
[7]周湘衡.端面模数为标准的斜齿轮测绘[J].机械传动,2003,27(5):49-51.

