齿根裂纹几何参数对齿轮强度影响的研究

余清，朱江新，黄伟，吴海浪

(广西大学机械工程学院，广西南宁530004)

0 前言

齿轮作为工程机械变速箱的重要组成部件，是工程机械再制造过程中的一个主要组成部分。齿轮回收件根据检测结果不同流向不同环节［1］，为了研究齿根裂纹几何参数对齿轮工作过程中应力集中情况的影响，将裂纹引入到齿轮副有限元分析模型中进行分析，对齿轮再制造具有重要意义。

1 齿轮几何模型的建立

以柳工ZL855 装载机变速箱输出轴齿轮对为研究对象，齿轮材料为20CrMnTi，弹性模量EX为2.07 ×1011Pa，泊松比0.25，抗拉强度1 080 MPa，屈服强度835 MPa，其具体参数见表1。

表1 ZL855 装载机变速箱输出轴齿轮对参数

首先在UG 软件中对齿轮副三维几何模型进行参数化建模，然后导入到Ansys 中进行有限元分析，为了提高计算效率，在不影响计算结果的情况下，对模型进行简化。简化过程中，一般认为离齿根的深度达到1.5m、宽度达到6m时(m为齿轮的模数)，齿轮体变形基本不再受影响，可以近似看作该处的实际位移为零［2］，简化后的齿轮副模型如图1所示。

图1 简化的齿轮三维模型

图2 危险截面示意图

2 齿根裂纹的引入

2.1 齿根危险截面的确定

要精确研究齿根裂纹对齿轮强度的影响情况，裂纹源出现位置的确定是关键。根据材料力学知识可知，构件最大内应力处强度最弱，是出现裂纹的危险截面。齿轮传动过程中，齿根部分承受较大弯曲应力作用，因此齿轮危险截面处于齿根处，目前主流的齿根危险截面的确定是根据Hofer 提出的30°切线理论［3］(与齿的对称中线成30°角作齿根曲线的切线，切点的连线AB即为齿根的危险截面)来确定，如图2所示。为了更准确地分析齿根裂纹对应力集中的影响，将裂纹沿齿根危险截面分布。

2.2 裂纹几何参数的确定

齿根裂纹的主要参数包括宽度、深度、长度以及分布位置。在齿根危险截面上，裂纹可能随机出现在任意位置上，为了研究不同分布位置的裂纹对齿轮强度的影响情况，文中在从动轮端部以及中部分别设置裂纹，其示意图如图3、图4所示。

图3 端部裂纹模型示意图

图4 中部裂纹模型示意图

齿轮回收件中的裂纹主要是疲劳裂纹或冲击裂纹，从裂纹产生到轮齿断裂过程中，裂纹经历着长度、宽度、深度3 个方向的扩展［4］。主要研究裂纹深度和长度对应力集中的影响，因此在齿根危险截面受拉一侧的端面处及中部分别创建一系列宽度为0.1 mm 的微小裂纹，为了系统研究裂纹在深度和长度方向对应力集中的影响，根据裂纹扩展路径［5-6］，在深度上选择0.1、0.2、0.3、0.4、0.5、0.6 mm 6 个值，长度上选择0.5、1、2、5、10、20 mm 6 个值，共建立72 个带齿根裂纹的有限元分析模型，并且假设齿轮模型除设定的裂纹外其他部分是连续且各向同性的。

3 齿轮三维静态有限元分析

为了提高计算精度以及适应带微小裂纹模型的网格划分，选择solid186 单元类型，采用自由网格划分方式，网格精度为6，主动轮划分为六面体网格，从动轮划分为四面体网格，如图5所示。

图5 有限元分析模型

单齿啮合区最高点是齿根弯曲应力最大的啮合位置［7］，为了分析齿跟应力分布，调整模型至刚好处于单齿啮合的最高点，在设置接触时，采用面接触，设置C1、C2、C3三个接触面，并且设置C2接触对自动闭合。

施加载荷约束时根据齿轮传动特性，在全局柱坐标系下，将A1、A2、A3三个面上的节点旋转至全局柱坐标系下，并限制轴向和径向自由度为0，而在A4、A5、A6三个面上施加全约束。为了施加贴近实际的载荷，将扭矩转换成节点力施加在主动齿轮内圈节点上。其中主动轮内圈半径为0.14 m，网格划分后内圈上的节点数为475 个，计算公式如下:

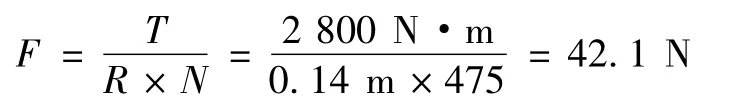
4 结果分析

通过有限元分析，可以得到无裂纹齿轮主、从动齿轮等效应力云图，如图6、7所示。

图6 主动轮等效应力云图

图7 从动轮等效应力云图

其中最大等效应力分别出现在主从动轮的齿根部分，主动轮最大等效应力108 MPa，从动轮最大等效应力为176 MPa，出现在齿根受压一侧，符合Hofer的30°切线理论，而从动轮齿根受拉侧的应力为108 MPa，说明分析方法是合理正确的。

图8—11 显示了不同分布位置的裂纹处的最大等效应力在裂纹长度和深度方向的变化情况。

图8 端部裂纹最大等效应力随长度变化情况

图9 中部裂纹最大等效应力随长度变化情况

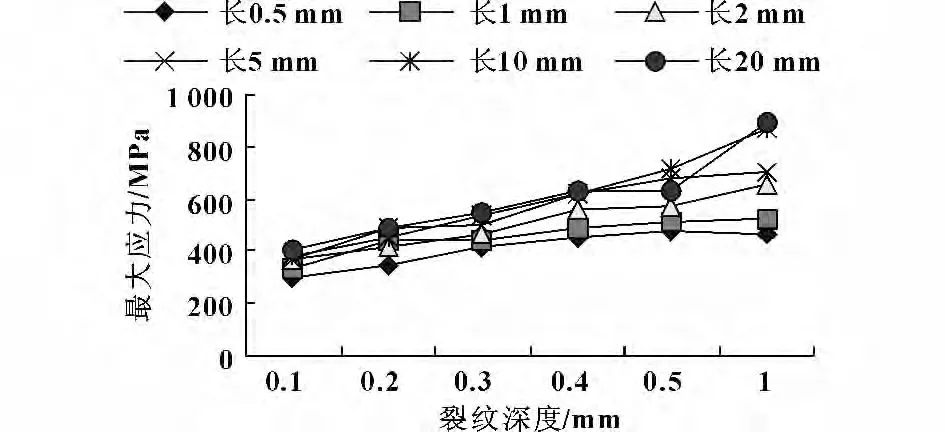
图10 端部裂纹最大等效应力随深度变化情况

图11 中部裂纹最大等效应力随深度变化情况

从图中数据可以得出以下结论:

(1)与无裂纹时齿根受拉侧最大等效应力108 MPa 相比，裂纹处的最大等效应力变化范围为301～890 MPa，因此齿根裂纹有明显的应力集中作用;

(2)根据图9 与图8、图11 与图10 的对比，在相同几何参数条件下，中部裂纹处的最大等效应力大于端部裂纹处的最大等效应力，因此中部裂纹对应力集中的影响较大;

(3)裂纹最大等效应力随深度变化曲线斜率比裂纹最大等效应力随长度变化曲线斜率大，因此裂纹深度对最大等效应力的影响比裂纹长度强。

5 结束语

使用有限元分析软件Ansys 对带裂纹的装载机变速箱输出轴齿轮对进行了静态三维接触分析。通过对设定了裂纹长度、深度及分布3 个不同参数的72 个带裂纹齿轮模型进行三维有限元分析，得到了不同裂纹处最大等效应力结果，通过图表形式对得到的分析结果进行对比研究，得出裂纹参数与裂纹处最大等效应力的相互关系，对给出齿轮裂纹极限判据具及对齿轮回收件再制造价值进行评估有重大的理论指导作用。

［1］张伟，刘仲谦，张纾，等.绿色制造与再制造技术研究与发展［J］.中国表面工程，2006，19(5):76-81.

［2］庄竞，袁卫华.TY320 型终传动齿轮有限元分析及结构改进［J］.工程机械，2006，37(10):31-34.

［3］李茹贞，赵清慧.齿轮强度设计资料［M］.北京:机械工业出版社，1984.

［4］DAVID G Lewicki，ROBERTO Ballarini.Gear Crack Propagation Investigations［J］.Tribotest，1998，5(2):157-172.

［5］David G，Lewicki.Effect of Rim Thickness on Gear Crack Propagation Path［J］.NASA Technical Memorandum 107229，1996.

［6］LALONDE S，GUILBAULT R.Prediction of Thin-rimmed Gear Crack Propagation From a Factorial Design Approach［J］.Fatigue ＆ Fracture of Engineering Materials ＆ Structures，201134(7):470-486.

［7］濮良贵，纪名刚.机械设计［M］.北京:高等教育出版社，2007.