面向绿色制造的切削速度优化选择研究

牛印宝，汪永超，王宇，王杰

(四川大学制造科学与工程学院，四川成都610065)

0 前言

切削速度的选择是机械加工过程中的一个重要环节，是切削用量三大要素之一，切削速度直接影响着加工时间、生产成本、刀具耐用度、能源消耗和加工质量［1］。在过去的加工过程中人们往往根据切削用量手册或者根据人工经验进行切削速度的选择，但是这种方法不能够进行切削速度优劣的定量计算和判断从而说服力不足，并且这种方法也很容易造成资源的浪费和生产效率的低下，这是不符合绿色制造的准则的。

面向绿色制造的切削速度的优化选择是一个十分复杂的过程，一般来说能够满足工业要求的切削速度有很多种，但是哪一种速度相对来说能够使加工时间最短、加工成本最低、能源消耗最少、环境污染程度最轻、刀具耐用度最长以及加工质量最好这是很难抉择的，要想解决这一问题就必须建立一个和切削速度有关的数学模型，并对数学模型进行优化以达到目的。文中在建立的数学模型基础上采用层次分析法和灰度关联法对模型进行分析和求解，这两方法相结合能够很好地对切削速度进行优化选择。

1 数学模型建立

1.1 指标函数的确定

通常，在对任何一个变量进行优化选择时都要有其一定的指标，否则优化就无从谈起。不仅如此，在文中使用到的层次分析法中必须要有指标作为其决策层，而且指标也必须要和待优化的变量有一定的关系。文中使用加工时间(Tv)、生产成本(Cv)、能源消耗(Rv)和刀具耐用度(T)作为数学模型的指标函数。在实际生产中加工的质量只要符合要求就行，不必要求质量越高越好，否则反而会增加不必要的成本，因此加工质量作为指标的作用不大，但是可以作为约束条件使用。在生产设备和生产方式确定的情况下制造业对资源的消耗主要是能源的消耗，并且能源的消耗和环境污染也是同向的，能源消耗的越少对环境的污染就越少。综上，只选择Tv、Cv、Rv、T4 项作为模型的指标函数。

1.1.1 加工时间

加工时间的函数表达式:

式中:tm为工序的切削时间;tl为工序过程中辅助时间;tc为一次换刀时间;T为刀具耐用度;L为切削长度;d为切削工件的直径;z为单面加工余量;Cr为刀具的耐用度系数;Kr为修正系数;m，xv，yv为对刀具耐用度的影响系数;f为进给量;ap为背吃刀量。

1.1.2 生产成本

生产成本指标函数可以表示为:

式中:M为单位时间内工厂的开支，主要包括的有劳动生产费和机床管理费;C为包括刀具的磨刀费、折旧费和更换费等相关的费用。

1.1.3 能源消耗

对于能源消耗它主要是以功率的形式体现出来的，故在此只需得到加工过程中功率消耗的表达式就可。在制造企业加工过程中消耗功率的方面有很多，主要的包括电机空转功率和切削加工的切削功率。具体的函数表达式如下:

式中:Pu为电机空载功率;Pc为切削功率;α 为功率平衡系数，其范围1.15～1.25;Fc为主切削力;CFc为与加工材料和切削条件有关的参数;为经验系数;为切削力修正系数。

1.1.4 刀具耐用度

刀具耐用度和生产效率以及生产成本有着密切的关系把它作为决策指标还是很有必要的，其函数形式如下:

1.2 模型的约束条件

在实际的生产过程中切削速度的选择还要受到很多条件限制，不能够随意选取。约束条件就像函数的定义域一样，规定了在优化选择时应该满足的基本条件。本模型切削速度的约束条件有如下几种:

(1)切削速度应该满足机床主轴转速的约束:

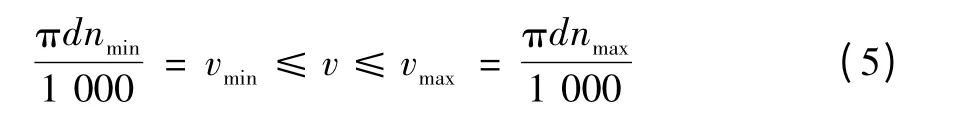
式中:nmin，nmax分别为机床主轴允许的最低转速和最高转速，d为切削工件的直径。

(2)切削力应小于机床主轴最大进给力:

式中:Fmax为机床进给机构允许的最大抗力。

(3)切削功率要小于机床的有效功率:

式中:η 为机床的传功功率，一般取η=0.75～0.85;Pmax为机床主电机传动功率。

(4)加工质量约束

工件表面的加工质量虽然和切削速度有关系，但是我们并没有把它加入到指标函数中而是把它作为约束条件，这样更显合理。

加工质量约束:

式中:R为工件表面粗造度;Rmax为工件允许的最大表面粗造度。

以上的几个约束条件是进行速度优化选择时必须要遵守的。假设有n个可供选择的切削速度方案，其中不满足上面约束条件的有m个那么只需对剩余的n-m个切削速度方案进行优化选择即可。

1.3 模型的描述

在以绿色制造为宗旨的加工生产中切削速度的选择是一件很困难的事情，因为切削速度影响着很多因素，其主要包括加工时间、加工成本、能源消耗和刀具的耐用度等。切削速度加大虽然能够使加工时间变短，但会增加能源的消耗以及刀具的磨损有可能还会加大成本;切削速度过小则会使加工时间增长，导致生产效率低下，这些都不能够满足绿色制造的要求。因此在对不同切削速度进行优化选择时一定要建立好数学模型［2］。假设有n中切削速度方案，那么切削速度的优化决策方案(X)可以用一个n维的列向量来描述，如下:

对此优化方案进行求解过程其实就是在满足式(5)、(6)、(7)、(8)的基础上求X*，使得

式中:Optimum(Tv(v)，Cv(v)，Rv(v)，T(v))为最优绿色性(加工时间最短、加工成本最少、能源消耗最少、刀具使用时间最长);v* 为最优的切削速度方案。

2 模型求解

由以上的分析不难看出面向绿色制造的切削速度的选择是一个典型的多属性、多目标的优化问题，里面的很多属性都难以定量分析，只能将定性分析和定量计算以及逻辑判断相结合的方式来解决这些问题。文中采用层次分析法结合灰色关联分析法来求解该模型。

2.1 使用层次分析法确定指标权重

层次分析法(AHP:Analytic Hierarchy Process)是由美国著名运筹学家萨蒂(T L SAATY)教授提出来的一种系统分析方法。这种方法把一个复杂的问题按照属性逻辑关系逐层分解，形成一个层次结构来加以分析，以简化问题的难度，并在逐层分解的基础上加以综合，给出复杂问题的求解结果［3］。

2.1.1 层次分析法的实施步骤

(1)建立层次结构图

首先要将评价的目标分解为各种组成因素，将这些因素再按属性关系分解为次级组成因素，如此层层分解形成一个有序的层次结构，如目标层O、指标层U、方案层A等。所设计的层次结构图如图1所示。

图1 层次结构图

(2)构造判断矩阵

针对上层要素Oi，假设U1，U2，…，Un是n个与Oi有关联的下层要素，要分析U层各要素针对Oi的相对重要程度，就可以构造一个n×n阶的判断矩阵，如表1。

表1 判断矩阵

在进行标度判断时传统的1—9 标度一致性比较差，故文中采用en/5标度来代替1—9 标度，两种标度的关系如表2。

表2 标度定义

(3)一致性检验

一致性检验是指判断矩阵中各个要素的重要性判断是否一致，不能出现矛盾。一致性判断的公式如下:

式中:C.Ⅰ.为一致性指标，值越小表明判断矩阵的一致性越好;λmax为矩阵的最大特征值;n为矩阵阶数;R.Ⅰ.为平均随机一致性指标，不同阶数的值可查表得到;C.R.为一致性比值，当C.R.＜0.1 时判断矩阵具有满意的一致性，若不满足此要求则要重新确立判断矩阵。

(4)确定指标权重

根据层次分析法原理，指标权重的确定就是求判断矩阵的特征根和特征向量，特征向量就是各指标的权重向量，特征值可以用来判断特征矩阵是否满足一致性，只有满足一致性所求的权重向量才有效。在层次分析法中一般采用近似计算的方法，常用的方法有“方根法”和“求和法”［3］，这里不再详细介绍具体公式。

有时，进行层次分析时其结构层次数不止一层，此时就要求出其最终权重集。假设上一层要素U1，U2，…，Um的权重已经确定，其数值为w1，w2，…，wm;且本层各要素A1，A2，…，An对Ui的各层权重结果为w1i，w2i，…，wni，那么本层最终的权重集为:

其中i=1，2，3…，m;j=1，2，3，…，n。

2.2 使用灰度关联法计算关联矩阵

在使用灰度关联法计算关联矩阵时，需要确定原始矩阵和参考指标体系、指标值无量纲化以及计算关联系数［5］。

2.2.1 原始矩阵和参考指标体系的确定

假设在一个优化问题中有n个备选方案，每个方案都有w个指标，那么就可构造出一个n×w的原始矩阵，如下:

参考指标在确定时应该遵循一个原则，即:它是从各个方案指标值中选取的最优值或者是常规下的理想值作为自己的指标数值。如果选取a0=［a01，a02，…，a0w］作为参考指标那么a01，a02，…，a0w都是参考指标中的最优值。

2.2.2 指标值量纲一化

由于不同指标的原始序列的量纲是不一致的，因此，需进行量纲一化处理以统一量纲。量纲一化的常见的方法有初始值法、均值化法和区间值化法。文中使用区间值法对指标进行量纲一化的处理，具体公式如下:

指标最优值为最大值时:

指标最优值为最小值时:

经过量纲一化处理后就可以得到如下的矩阵:

此时前面选取的参考指标就变成了e0=［1，1，…，1］。

2.2.3 计算关联系数

关联系数的意义就是比较各方案指标和理想指标之间的关联程度，公式如下:

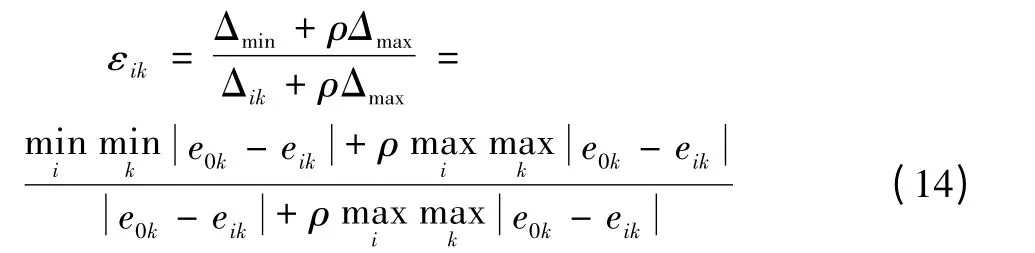
式中:ρ 为分辨率，ρ=0～1，一般取0.5 为宜［4］。

事实上经过量纲一化之后，上述公式可以简化为:

关联系数求出之后，就可得到关联矩阵，如下:

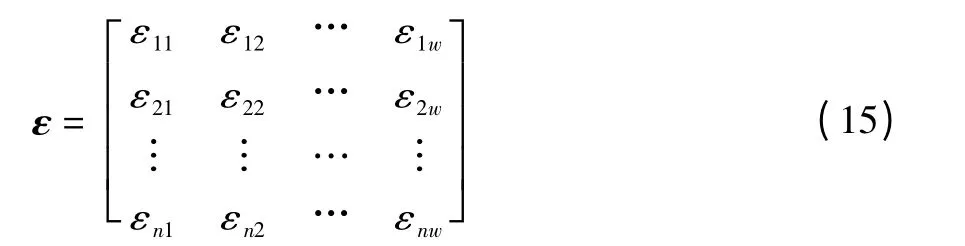
2.3 计算关联度

关联度的计算是切削速度进行优化选择时的关键步骤，只要计算出了各个方案相对于最优方案的关联度，就可直接定量的比较出那种方案是最符合绿色制造要求的，即绿色度最高的。

关联度的计算就是将上面求到的最终权重集引入到关联矩阵中，公式如下:

式中:Q为可比较的数据集;ε 为关联矩阵;W 为指标的权重向量。

从上述公式就可以得到一个与最优方案有关的数据集，经过比较它们值的大小就可确定哪种方案和最优方案最接近，即为最优切削速度方案［6］。

3 结束语

所研究的切削速速度的优选方法在理论上有很强的可行性，对于某些评价方案来说它们的指标值都是通过经验判断或模糊处理得到的，这有一定的误差，而文中的指标值都是由公式直接得到，不会有人为的误差，而且文中采用的是改进标度的层次分析法能够使计算出来的结果具有更高的准确性。此外在进行模型求解时，可以使用MATLAB 工具，在MATLAB 中建立实现此功能的M 文件，只需将要比较的切削速度输入进去就可判断哪一个绿色度最高。此方法方便快捷可以很好地解决切削速度难选择的问题，与传统的方法相比更高速、精密、清洁，完全符合绿色制造的要求。

［1］王杰，李方信，肖素梅.机械制造工程学［M］.北京:北京邮电大学出版社，2003.

［2］江志刚，张华.绿色制造企业生产过程多目标集成决策指标体系研究术［J］.机械设计与制造，2008(8):232-234.

［3］谢家平.绿色设计评价与优化［M］.武汉:中国地质大学出版社，2004.

［4］李友宾，李苗苗，路世昌.基于层次-灰色关联分析的虚拟企业战略伙伴选择［J］.辽宁工程技术大学学报:社会科学版，2006，8(1):59-61.

［5］陈婀娜.基于灰色系统理论的数控机床选型决策［J］.微机计算机信息，2006，22(6):138-139.

［6］于志慧，丁毅.基于灰色综合评价法的包装评价模型研究［J］.包装工程，2012，33(3):59-62.