立式数控铣床主轴-刀柄和刀柄-刀具结合面参数辨识方法的研究

孙新国，孙亮，王二化

(1.南阳理工学院机械与汽车工程学院，河南南阳473004;2.河南工业职业技术学院，河南南阳473000)

0 前言

随着制造技术的不断发展，高速切削日益成为制造行业中的一项关键技术，在减少工件变形、提高产品质量和加工效率方面具有无可比拟的优越性。其中，切削颤振是制约高速切削技术快速发展的一个重要因素，它不仅会限制机床的生产率，而且会严重影响工件表面质量，大大加剧刀具磨损，极端恶化工作环境。因此，为提高立铣加工过程稳定性，通常利用稳定性Lobe 图来确定切削过程中稳定和不稳定的切削区域。研究发现，机床出现的振动问题有60%以上源自结合部的刚度和阻尼，总阻尼值的90%以上源自结合部的阻尼。目前，主轴-刀柄和刀柄-刀具结合面参数辨识方法还不成熟，因此，主轴-刀柄和刀柄-刀具结合面参数辨识是高速立铣加工过程中亟需解决的关键问题之一。

固定结合面参数辨识方法研究者众多，但由于固定结合面的复杂性与多样性，目前还没有出现一种成熟通用的辨识方法。常用的优化方法有牛顿法、遗传算法、蚁群算法、退火算法和粒子群算法等。由于粒子群算法原理简单，容易实现，较适合应用于连续优化问题求解，但该算法较容易陷入局部最优问题，因此，为了提高主轴-刀柄和刀柄- 刀具结合面参数辨识精度，文中采用融合粒子群和局部搜索算法的优化算法实现主轴-刀柄和刀柄-刀具结合面参数辨识。

粒子群优化算法是由Kennedy 和Eberhart 于1995年最早提出的一种演化计算技术，同遗传算法一样，粒子群也是一种群体迭代算法，但没有遗传算法中的交叉和变异，不需要编码和解码［1-2］，并且需要调整的参数不多。柔度耦合子结构分析(Receptance Coupling Substructure Analysis，RCSA)和改进型粒子群优化算法(Particle Swarm Optimization，PSO)是一种处理优化问题的较好的算法［3-4］，在很多领域中均得到了广泛应用。

局部搜索算法(Local Neighborhood-searching，LNes)是针对平面局部密集结点提出的一种算法［5］，该算法利用确定的圆形搜索域在优化空间中进行密集点搜索。

1 主轴-刀柄和刀柄-刀具结合面的参数辨识及实验研究

以XHK 立式加工中心为研究对象，进行主轴-刀柄和刀柄-刀具结合面参数辨识研究。刀柄和刀具的材料密度为7.8 × 103kg/m3，杨氏模量E=200 GPa，尺寸如图1所示。

图1 刀柄和刀具尺寸

通过基于Timoshenko 梁的传递矩阵法，计算刀柄和刀具端点频响函数，可以得到刀柄和刀具所有的直接和交叉端点频响函数［6-8］。其中，刀柄部分直接和交叉频响函数如图2—5所示。

图2 刀柄直接端点频响函数

图3 刀柄交叉端点频响函数

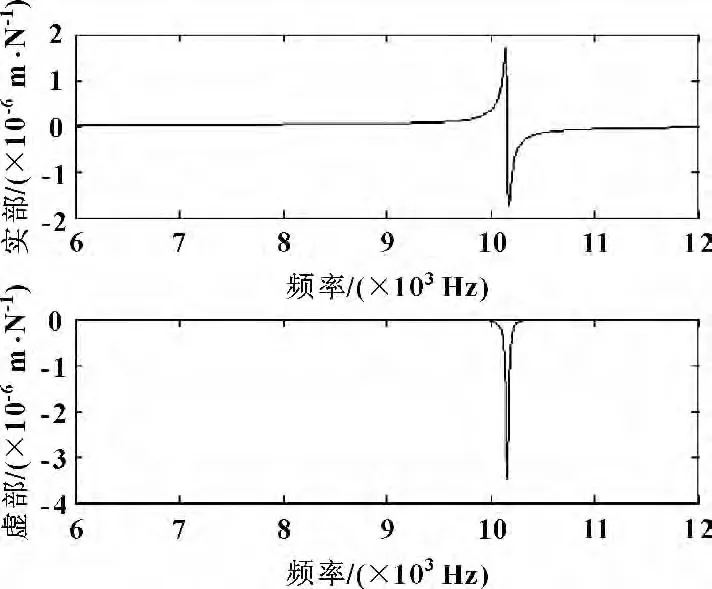
图4 刀柄交叉端点频响函数

图5 刀柄直接端点频响函数

从图2—5 可以看出，刀柄第一阶弹性模态介于10 000～11 000 Hz 频域范围之间。刀具部分直接和交叉频响函数如图6—9所示。

图6 刀具直接端点频响函数

图7 刀具交叉端点频响函数

图8 刀具交叉端点频响函数

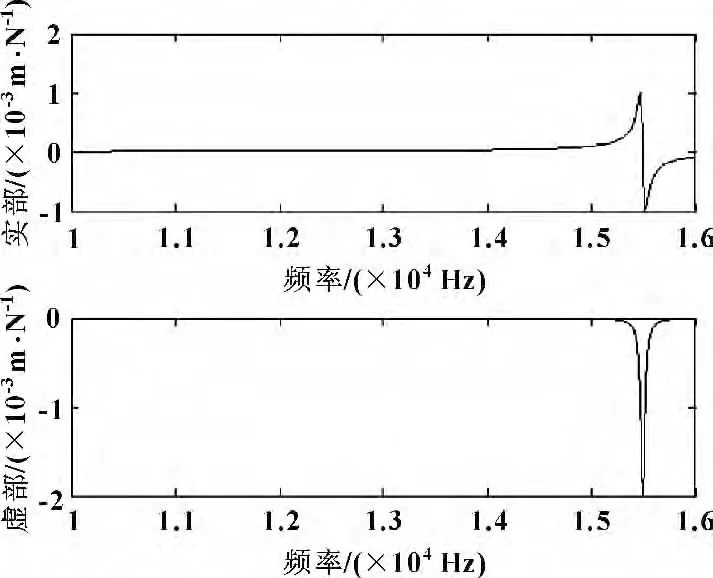
图9 刀具直接端点频响函数

从图9 可以看出，刀具第一阶弹性模态介于15 000～16 000 Hz 之间，刀具端点频响函数对加工中心刀尖频响函数会有较大影响。

如上所述，由于主轴装配体具有复杂结构，文中利用激振测试方法获取其端点频响函数，实验装置如图10所示。

得到各子结构端点频响函数后，基于RCSA 方法，利用直线和转动弹簧阻尼单元将3 个子结构耦合起来，进行XHK 加工中心刀尖频响函数预测。其中，主轴-刀柄和刀柄-刀具结合面参数是需要辨识的未知量。

为了识别主轴-刀柄和刀柄-刀具结合面参数，通过激振实验方法测试XHK 加工中心刀尖频响函数，实验装置如图10(b)所示。将加速度传感器固定在刀具底端，同时利用力锤敲击刀尖位置获取激振力和加速度信号，将采集到的信号传输到LMS 数据采集系统，采用谱分析技术获取刀尖位置的直接和交叉频响函数。同样，为了提高刀尖频响函数测试精度，在相同条件下，连续测试5 次取平均值。

图10 实验装置

图11 主轴装配体直接端点频响函数

图12 主轴装配体直接端点频响函数

基于RCSA 耦合算法，通过直线、转动弹簧阻尼单元耦合主轴装配体、刀柄和刀具3 个子结构，得到预测的刀尖频响函数。考虑到辨识算法中含有大量的矩阵运算，选择擅长矩阵运算的Matlab 软件进行编程，实现主轴-刀柄和刀柄-刀具结合面参数的辨识。运算时间取决于方程的数量、频域范围和单位频率内的频率点数。利用指定的计算机(Pentium®Dual-Core CPU 2.93 GHz，2.0 GB RAM)进行计算，完成主轴-刀柄和刀柄-刀具结合面参数的辨识，耗时31 min，辨识出的结合面参数如表1所示。

表1 辨识出的主轴-刀柄和刀柄-刀具结合面参数

为了验证文中提出的主轴-刀柄和刀柄-刀具结合面参数辨识算法，将辨识出的各个结合面参数代入到刀尖频响函数预测模型中，得到预测的刀尖频响函数，将其和测试的刀尖频响函数进行对比如图13所示。

图13 测试和预测的机床刀尖频响函数

可以看出，除了在频率1 200 Hz 峰值附近有一些波动外，预测和测试的刀尖频响函数具有较好的一致性。较好的预测结果说明，文中提出的辨识算法能有效辨识主轴-刀柄和刀柄-刀具结合面参数。

为了验证辨识算法的普适性，改变刀具悬臂分别长度为90，100 和110 cm，分别称为案例2，3 和4。利用文中提出的方法，辨识不同悬臂长度情况下的主轴-刀柄和刀柄-刀具结合面参数，并将预测与测试刀尖频响函数进行比较。为了量化预测和测试刀尖频响函数的一致性，基于误差向量E，构造预测的刀尖频响函数的平均误差表达式如下

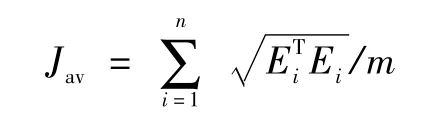
式中:m是频率测试点数;Ei是误差向量E的第i个元素。

这4 组案例的平均误差结果如表2所示。

表2 各组案例预测和测试刀尖频响函数的平均误差

从表2 可以看出，对于不同的刀具悬臂长度，预测和测试的刀尖频响函数都具有较好的一致性。

2 结束语

对于不同的刀具悬臂长度，主轴-刀柄和刀柄-刀具结合面参数都能得到较高精度的辨识，论证了所提出的辨识算法的普遍性和适用性。因此，该辨识算法可以应用与文中研究对象具有相似结构的主轴-刀柄和刀柄-刀具结合面参数辨识研究过程中。

［1］王越，曾晶，董丽梅，等.基于粒子群的BP 神经网络算法在猪等级评定中的应用［J］.重庆理工大学学报，2013，27(1):37-41.

［2］王红玲，郑纲，何剑锋.基于改进粒子群算法的生鲜农产品配送路径优化研究［J］.安徽农业科学，2010，38(31):17961-17962.

［3］柴银刚.基于导纳耦合法的高速电主轴-夹具-刀具系统动态特性分析和铣削稳定性研究［D］.上海:上海交通大学，2013.

［4］王旖旎.基于PSO 的图像增强算法研究［D］.重庆:重庆师范大学，2012.

［5］詹青青.启发式局部搜索算法在电路划分中的应用［J］.福建电脑，2010(2):112-113.

［6］毛宽民，黄小磊，田红亮，等.机床固定结合面参数识别及其拟合方法［J］.华中科技大学学报:自然科学版，2011，39(3):18-21.

［7］尤晋闽，陈天宁.结合面法向动态参数的分形模型［J］.西安交通大学学报，2009，43(9):91-94.

［8］李娜.格上传递矩阵和模糊矩阵的性质［D］.成都:四川师范大学，2008.