基于液压传动的海洋波浪换能系统功率解耦特性研究
崔晓,程永强
(山东省科学院海洋仪器仪表研究所,山东青岛266001)
0 前言
海洋波浪能是以机械能形式存在于海水中的取之不尽的可再生能源,它是包括潮汐能、海流能、波浪能、温差能、盐差能等在内的海洋能中品位最高的能量[1]。海洋波浪换能装置的作用是把俘获的波浪能转换为某种特定形式的机械能或液压能。根据海洋波浪的特点,一般波浪捕获装置要求在低速、变速、大扭矩的工况下运行,而发电设备要求在较高的转速下单向恒速旋转运动,这就要求换能系统能够实现增速、功率传递和控制等功能。根据国内外目前的研究状况,普遍采用3 种能量转换方式:齿轮变速箱式、直驱式、液压传动式。齿轮变速箱传动方式其传动比单一,不能平缓海流冲击,会影响发电机的寿命。而直驱传动方式,鉴于目前低速永磁同步发电机技术不够成熟及海洋环境的恶劣性,成本较高。液压传动具有传动功率大、结构小、响应速度快、可以实现无级变速等优点,且易实现过载保护,非常适合低速、大扭矩的场合应用,已成为波浪换能装置的首选传动方式[2]。基于这一原理的海洋波浪换能系统主要由能量捕获装置、液压泵、液压马达、蓄能器、流量及压力控制单元等元件组成。能量捕获装置将波浪能转换为不稳定的机械能并驱动液压泵工作,泵输出液压能并经由流量控制单元整流为单一方向的液压能。压力控制单元及蓄能器将不稳定的液压能转换为稳定的液压能并驱动液压马达带动发电机恒速运转,输出稳定电能。
波浪能的能量产生是由自然条件及地理环境决定,能量变化的幅值及频率随机性较大,所以利用波浪能产生的能源电力输出一直被认为是“垃圾电”,而且由于输入功率的不稳定、不连续,甚至是快速突变的,其对发电装置的机械结构会产生不同强度和不同变化率的冲击力,大大影响了机组的稳定性和可靠性[3]。解决这一问题的关键在于实现波浪换能装置液压传动系统输入与输出的功率解耦及阻尼调节。通过对传动系统的控制使输入的压力、流量与输出的压力流量并不直接耦合,在输入与输出之间提供储能单元将多余的能量储存起来并在合适的时机释放,这应成为波浪换能装置传动系统应具备的重要功能。目前,国内外对于波浪换能装置液压传动系统的研究大多集中在应用先进控制策略提高能量利用效率和提高传动系统可靠性方面,大多采用大容量蓄能器与调速阀平稳流量与压力波动实现输入输出的功率解耦。文献[4]分析了变压力系统与恒压力系统在传动效率和速度调节特性上的差异,分别建立了两种传动系统的数学模型。文献[5]针对波浪能转换应用而设计一种新型数字液压泵/液压马达,具有很高的换能效率。文献[6]对换能装置传动系统的各种非线性控制方法进行了综合与比较,提出应用最优控制策略的思想。文献[7]对英国OPT 公司开发的Pelamis 波力发电装置从原理上进行了详细的阐述,Pelamis 通过角位移驱动液压缸实现了波浪能到液压能的转换,采用大容量蓄能器实现了输入功率与输出功率的解耦及能量存储。Pelamis 是一个典型的对非稳定功率输入进行调速的液压传动系统,Pelamis 的成功也为液压传动在海洋波浪换能上的应用奠定了良好的基础。
针对功率解耦的问题,本文作者提出了一种换能装置液压传动系统,该系统根据液压变压器原理,将定量马达与变量泵连轴,根据捕能液压缸的输入位移实时调整变压比稳定液压马达输出转速,同时使用蓄能器进一步平稳压力波动,实现变压网络到恒压网络的转换,解决液压传动系统输入与输出的功率解耦问题。
1 液压传动系统组成及工作原理的理论分析
1.1 传动系统的组成
独立稳定波浪换能装置液压传动系统主要由波浪能捕获装置、液压缸、整流单元、压力能变压单元、蓄能器、马达及发电机组成。如图1所示,整个系统分为能量捕获单元、整流单元、调压单元、蓄能单元和发电单元,通过对液压能的整流、调压和蓄能将不稳定功率输入的变压网络转换为能够稳定驱动发电机负载的恒压网络。可以看出与以往波浪换能装置液压传动系统不同的是,该传动系统通过增加变压单元及使用两套独立的液压回路实现输入与输出功率的解耦。

图1 波浪换能装置液压传动系统基本组成
1.2 传动系统工作原理的理论分析
图2所示为所设计的液压传动系统工作原理图,能量捕获装置(浮子)在波浪能的驱动下往复运动,带动液压缸cy1往复运动输出压力油。由4 个单向阀c1~c4构成的液压整流单元可以将双向液压油转换为单一方向泵入液压马达M1,液压马达M1再驱动与其连轴的变量液压泵Mp送出高压油驱动另一液压马达M2,液压马达M2带动发电机G 保持恒速转动,输出稳定电压。溢流阀r1、r2及r3起到保护及调定系统压力的作用,蓄能器Acc1用来吸收压力和流量脉动,稳定功率输出的作用,而由测速泵p1和液压缸cy2构成的转速控制回路用来实时调整变量泵Mp的排量,改变液压变压器的变压比,这也是该液压系统实现输入—输出功率解耦的关键。
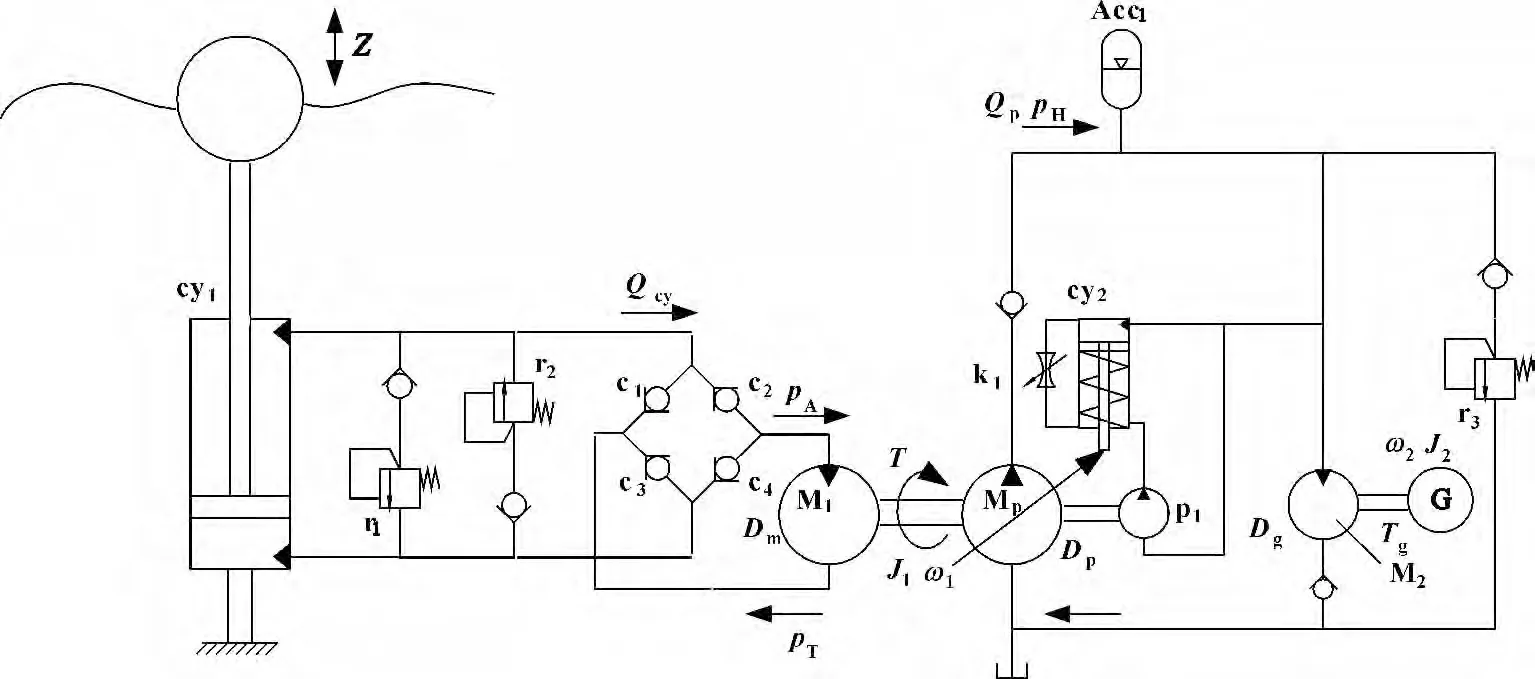
图2 波浪换能装置液压传动系统输入输出功率解耦原理图
在对该液压传动系统进行理论分析时,首先做如下假设:
(1)忽略马达、泵、液压缸及蓄能器等液压元件的容积损失和机械损失。
(2)认为马达与变量泵之间及马达与发电机之间的连轴为刚性连接。
(3)忽略变量泵变量机构的动态效应。
(4)通往油箱的回油压力为零。
(5)忽略流体介质的可压缩性。
设该液压传动系统工作在稳定状态下,对于由泵Mp和马达M2构成的泵控系统来说,泵Mp的流量方程为:

式中:Qp为泵Mp输出流量,ω1为泵Mp转速,Dp为泵Mp弧度排量,ctp为泵Mp的泄漏系数,pH为泵Mp输出压力。
对泵Mp和马达M2构成的液压回路,根据流量连续性方程可以得到:

式中:ω2为马达M2的输出转速,Dg为马达M2弧度排量,ctm2为马达M2的泄漏系数。
由马达M2的力矩平衡方程可得:
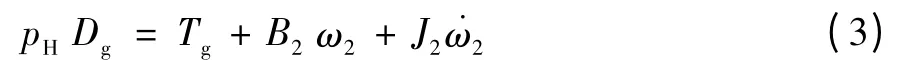
式中:Tg为发电机G 负载转矩,J2为马达M2与发电机转轴上所有部件总的转动惯量,B2为马达M2与发电机转轴上的黏性阻尼系数,ω2为发电机转速。
将式(1)到式(3)取拉氏变换,将式(3)代入式(1)和式(2),消去pH得到马达M2输出转速与泵Mp输入转速之间的关系:
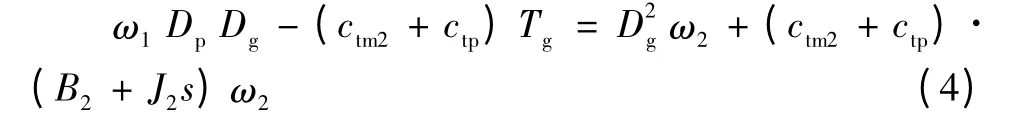
令ct=ctm2+ctp为泵控液压系统总的泄漏系数,可以得到:
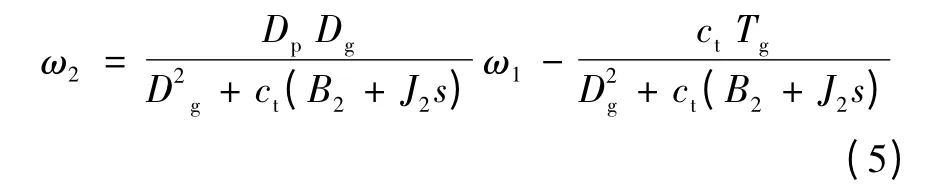
同理可以列出液压缸cy1与马达M1构成回路的流量连续性方程:
2 液压传动系统的仿真分析
为进一步分析所设计换能装置液压传动系统在不同海况下的工作特性,验证传动系统对于输入—输出功率解耦的有效性,对系统的稳态特性、波动特性及换能效率进行了仿真研究,利用AMESim 的液压库来搭建该液压传动系统的模型,利用Matlab 建立波浪换能装置的水动力学模型,在此基础上进行联合仿真验证所设计液压传动系统的有效性。
2.1 模型的建立
所建立的波浪换能装置液压传动如图3所示。模型中能量捕获装置的水动力学模型由基于线性波理论的F-K 方法建立[8],如式(7)—(8)所示。

图3 换能装置液压传动系统仿真模型
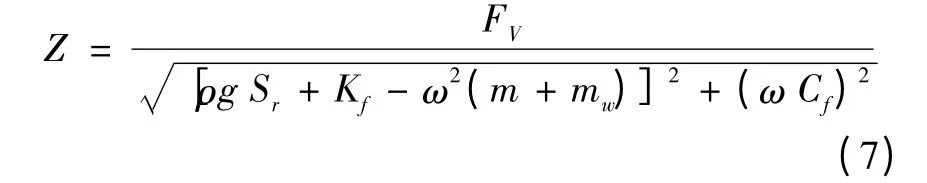
式中:Z为浮子在波浪力作用下产生的位移;FV为作用在浮子上的波浪力,由文献[9]根据F-K 方法可计算得出;ρ 为海水的密度,g为重力加速度,Sr为浮子的水线面积,ω 为波浪起伏圆频率,(m+mw)为浮子及其附加的海水质量,系数Kf和Cf分别为等效弹性系数和等效阻尼系数,可根据式(8)由液压缸输出力Fcy计算求得。
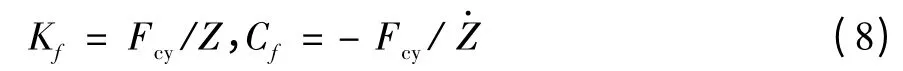
波形数据也是应用线性波理论根据线性叠加法模拟而生成[10],文中选取振幅2 m、波形系数0.8 和波动频率为10 的波浪数据。将计算出的初始状态液压缸对浮子输出力代入式(7)及式(8)可求得浮子位移Z,对位移求导得到液压缸的输入速度并带回模型中计算下一时刻液压缸输出力,如此反复迭代下去就可以完成整个模型的仿真过程,模型中的各仿真参数如表1所示。

表1 换能装置液压传动系统仿真参数
2.2 仿真结果
如图4所示为与液压缸相连接的能量捕获机构在波浪力作用下的位移响应曲线,图5 为能量捕获机构的速度响应曲线。根据仿真模型中液压缸的输出流量和压力可以计算出输入到液压传动系统中的瞬时功率及平均功率,也可以根据传动系统输出力与能量捕获机构速度的乘积计算出输入到系统中的总功率。文中采用了第一种方法,计算出并归一化的输入系统瞬时功率曲线如图6 中曲线1所示,平均功率为图6 中虚线2所示。从图中可以看出,输入到系统中的功率波动是比较大的,其峰值功率为平均功率的7.41 倍,且有80%的时间中对系统的输入功率都在平均功率以下,若考虑到马达、泵的效率以及某些极端海况的条件下,峰值功率与平均功率之比可能会更大。这就给传动系统的设计带来了很大的困扰,若按照平均功率设计系统,则无法保证在峰值功率时系统的可靠性和安全性,若按照峰值功率来设计并选择液压元件会造成传动系统的工作效率低,无法使其工作在最佳状态,这也充分说明了换能装置中功率解耦的必要性。

图4 能量捕获机构位移曲线
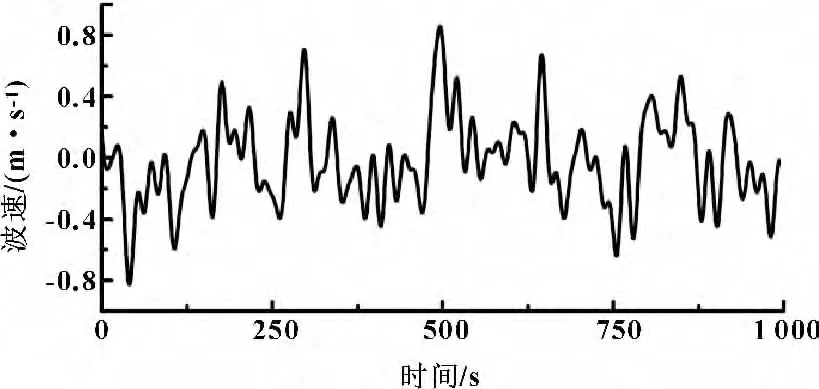
图5 能量捕获机构速度曲线
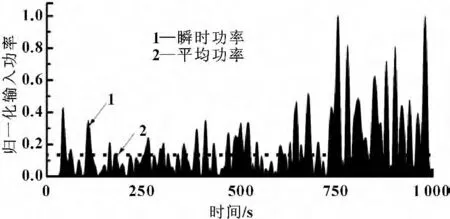
图6 传动系统输入功率归一化曲线
如图7所示为经过液压变压实现功率解耦后马达M2的输出功率曲线,可以明显地看出液压传动系统的输出功率较输入功率相比已经平稳了很多,峰值功率仅为平均功率的1.01 倍,且95%以上的时间内系统的输出均为平均功率。组成液压变压器的变量泵Mp实际排量与最大排量之比的变化过程如图8所示,可以看出液压缸cy2通过检测流量变化实时变量泵Mp变量机构,使其保持相对恒定的功率输出。值得注意的一点是在最小排量和最大排量之间频繁的改变不利于延长液压元件的寿命,也对变量泵的性能和可靠性提出了一定的要求。
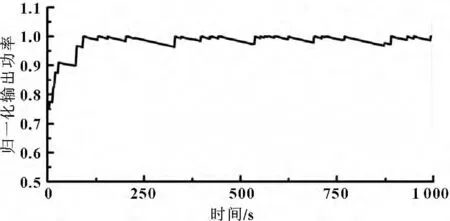
图7 马达M2 输出功率归一化曲线

图8 变量泵Mp 实际排量与最大排量比变化曲线
图9所示为驱动发电机的液压马达M2的输出转速曲线。可以看出通过传动系统功率解耦作用以及在液压蓄能器缓冲的共同作用下,可以得到一个相对比较稳定的发电机驱动转速。马达M2的输出转速保持在650~700 r/min 之间,进而可以实现恒频稳压的发电需求。图10所示为定量马达M1和变量泵Mp两腔压差随时间变化曲线,图11所示为定量马达M1和变量泵Mp输出流量随时间变化曲线。可以看出在由马达—泵所构成的液压变压器的作用下,将低压、大流量的功率输入转换成为高压、小流量的功率输出。同时,实现了将非稳定功率输入的变压网络转换为能够稳定驱动发电机负载的恒压网络。
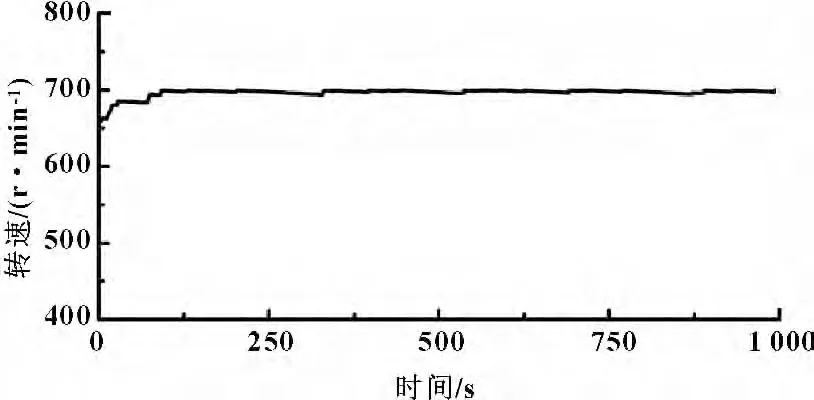
图9 马达M2 输出转速随时间变化曲线
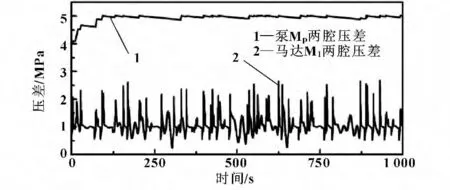
图10 马达M1 和泵Mp 输出压力差随时间变化曲线
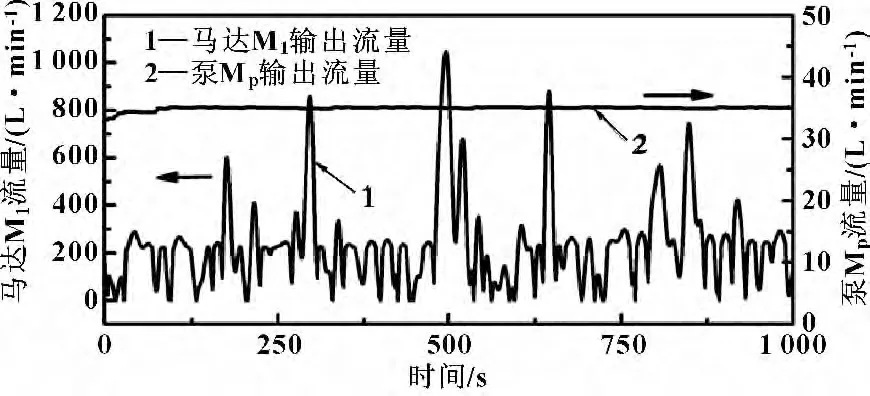
图11 马达M1 和泵Mp 输出流量随时间变化曲线
4 结束语
针对海洋波浪换能装置中传动系统输—输出功率耦合的问题,提出了一种基于液压变压器原理的液压传动系统设计方案。通过将以低压、大流量为特点的变压网络转换为以高压、小流量为特点的恒压网络,实现了传动系统输入与输出功率的解耦。叙述了传动系统的组成,理论推导了系统的工作原理。进一步建立了基于AMESim 的系统数学模型并进行了计算机仿真。仿真模拟了典型海况输入下传动系统的响应。其结果表明,驱动发电机负载的马达转速及输出功率基本平稳,可以实现恒频稳压的发电需求。该方案可应用于海洋波浪能的开发,同时也可广泛应用于风能、潮汐能等非稳定功率输入系统中,并对闭式液压回路的功率调节特性研究产生积极的影响。
[1]肖惠民,于波,蔡维由.世界海洋波浪能发电技术的发展现状与前景[J].水电与新能源,2011,1(10):67-70.
[2]DREW B,PLUMMER A R,SAHINKAYA M N.A Review of Wave Energy Converter Technology[C].Proc.IMechE Vol.223 Part A:J.Power and Energy,2009,223(14):887-902.
[3]张大海.浮力摆式波浪能发电装置关键技术研究[D].杭州:浙江大学机械工程学院,2010:13-14.
[4]COSTELLO Ronan,RINGWOOD John V,WEBER Jochem.Comparison of Two Alternative Hydraulic PTO Concepts for Wave Energy Conversion[J].Ocean engineering,2007:2021-2032.
[5]PAYNE G S,KIPRAKIS A E,EHSAN M,et al.Efficiency and Dynamic Performance of Digital DisplacementTMHydraulic Transmission in Tidal Current Energy Converters[C].Proc.IMechE Vol.221 Part A:J.Power and Energy,2007:207-218.
[6]CRETEL J A M,LIGHTBODY G,THOMAS G P,et al.Maximisation of Energy Capture by a Wave-Energy Point Absorber using Model Predictive Control.18th International Federation of Automatic Control(IFAC),2011:3714-3721.
[7]HENDERSON Ross.Design,Simulation and Testing of a Novel Hydraulic Power take-off System for the Pelamis Wave Energy Converter[J].Renewable Energy,2006,31(9):271-283.
[8]程晨.面向海洋机器人的浮子式波浪能发电装置研究[D].长沙:国防科学技术大学机械工程学院,2011.
[9]CORMICK M,MODIFIED M E.A Modified Linear Analysis of a Wave Energy Conversion Buoy[J].Ocean Engineering,1976,3(3):133-144.
[10]聂卫东,康凤举,褚彦军,等.基于线性海浪理论的海浪数值模拟[J].系统仿真学报,2005,17(5):1037-1039.

