Dirichlet函数在实变函数中的应用

张安玲

（长治学院 数学系，山西 长治 046011）

Dirichlet函数的一般表达式是

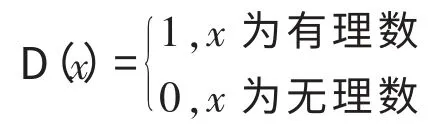
该函数是定义在全体实数R 上的函数，它在上任意点处极限不存在，从而在R 上处处不连续；在定义域R 上是个偶函数；在任意区间（α，β）内都不具有单调性；任何有理数r＞0都是它的周期，但Dirichlet函数没有最小正周期；Dirichlet函数无对称中心但有无数条对称轴[1]。Dirichlet函数具有的这些性质使得它在教学中起到了重要的作用。

实变函数论是19世纪末、20世纪初，主要由法国数学家勒贝格(Lebesgue)创立的[2]。它是普通微积分学的继续，其核心内容是Lebesgue测度与Lebesgue积分，Lebesgue测度与Lebesgue积分理论的产生来自于对Riemann积分的改良[2]。实变函数内容抽象、方法巧妙，许多概念、定理、结论都很难理解，而Dirichlet函数在实变函数中经常作为独特的例子出现。通过Dirichlet函数可以加强对实变函数中某些知识点的理解。

1 简单函数

定义：设f（x）的定义域E 可分为有限个互不相交的可测集，使f（x）在每个Ei上都等于某常数Ci，则称f（x）为简单函数[2]。

理解简单函数这个概念要抓住以下几点：

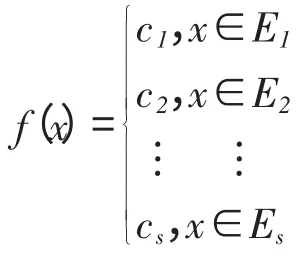
其中Ei（i=1,2,…s）是可测集，Ei∩Ej=○且E=这样的函数f（x）为简单函数。

有理数集Q是可测集，RQ 是可测集，Q ∩（RQ）=○且R=Q∪（RQ），当x∈Q时D（x）等于常数1；当x∈RQ 时D（x）等于常数0。所以Dirichlet函数是简单函数。

通过Dirichlet函数这个例子，进一步加深了对“简单函数”的理解。

2 几乎处处成立

几乎处处成立是实变函数中非常重要的概念，它对进一步理解几乎处处收敛、几乎处处连续、几乎处处有限等概念以及叶果洛夫定理、鲁津定理、里斯定理、勒贝格定理等定理有很大的作用。

定义：设π 是一个与集合E 的点x 有关的命题，如果存在E 的子集M，满足mM=0，使得π 在EM 上恒成立，也就是说，EE［π 成立］是零测度集，则称π 在E 上几乎处处成立，或者说a.e.于E[2]。

从以下几点理解几乎处处成立这个概念：

1）M⊆E，mM=0；

2）π 在EM 上恒成立；

则称π 在E 上几乎处处成立。

D（x）=0在RQ恒成立；Q⊆R，且mQ=0，即使得D（x）≠0成立的集合的测度为0，所以D（x）=0 a.e.于R。

3 可测函数与连续函数的关系

可测函数与连续函数有着密切的联系。可测集上的连续函数都是可测函数，但是可测函数不一定是连续函数[2]。如Dirichlet函数。而鲁津定理揭示的是，在E 上a.e.有限的可测函数是“基本上连续”的函数[2]。

对任意有限实数a，有

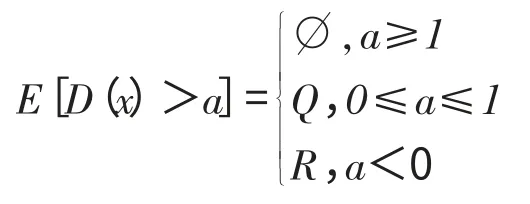
4 Riemann可积与Lebesgue可积的关系

如果有界函数f（x）在闭区间［a，b］上Riemann可积，则f（x）在［a，b］上Lebesgue可积，但其逆命题不成立。即若f（x）在闭区间［a，b］上Lebesgue可积，f（x）在［a，b］上不一定Riemann可积[3]。如Dirichlet函数。

Riemann积分用“内填外包法”：将定义区间分割为小区间；然后以小区间Δi的长度为底，函数在Δi上的下确界mi为高的那些矩形内填，还以Δi的长度为底，函数在Δi上的上确界Mi为高的那些矩形外包；当把区间分得很细时，内填外包的矩形面积之差可以无限小，彼此都趋于一个定值时，函数就是Riemann可积的[2]。

Dirichlet函数不管把定义域划分成多么小的n个区间，每个小区间里都有无理数和有理数，函数值分别取值0和1，它们彼此之差处处都是1，不会趋于相同的值，于是Dirichlet函数是Riemann不可积的[2]。

Lebesgue积分是将函数的值域分割成小区间，把函数值相差不多的那些点集放在一起，用横放着的小矩形面积之和加以逼近[2]。

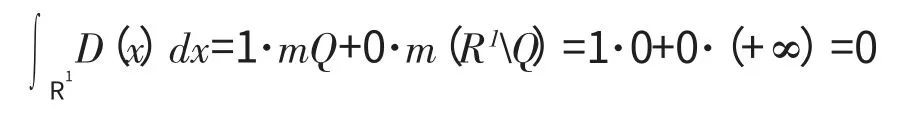
Dirichlet函数是Riemann不可积的，但它是Lebesgue可积的，这说明Lebesgue积分是比Riemann积分范围更广的一种积分。

5 结束语

实变函数论中概念、定理、结论很多，而且都很抽象，关系也很复杂，理解起来非常困难。在学习简单函数、几乎处处成立、可测函数与连续函数的关系、Riemann可积与Lebesgue可积的关系时引进Dirichlet函数，使得能轻松搞清楚一些复杂关系、深化对概念的理解，对学习实变函数起到很大的作用。

［1］李景廉.函数在实变函数中的应用［J］.佛山科学技术学院学报,1999,17(3):67-70.

［2］程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础［M］.高等教育出版,北京:2010.

［3］刘京鑫.反例在实变函数中的运用［J］.高等数学研究,2009,12(4):117-121.