基于色散器件的原子光谱实验研究

王铁云，张 翠

（长治学院 电子信息与物理系，山西 长治 046011）

1 引言

牛顿在1704年就曾说：“若想了解原子的内部结构，只要看光谱就可以了”。光谱的研究已有几百年的历史，最早研究的是氢原子光谱，然后又有碱金属与铁原子等原子光谱的研究。众所周知，白光经过光学色散器件后可以看到七种不同颜色的光线，而每一条光线都有与之对应的折射率与波长。文章采用三棱镜作为色散器件，对汞、氦、氖等的原子光谱进行定性研究，通过测定汞灯各条谱线的数据，拟合定标曲线，由定标曲线确定氦灯、氖灯光谱各条谱线的波长。

2 原子光谱与色散器件

2.1 原子光谱理论概述

原子光谱是由原子中的电子在能量变化时所发射或吸收的一系列光所组成的光谱。不同原子的光谱各不相同，氢原子光谱最为简单，其他原子光谱较为复杂，最复杂的是铁原子光谱。早在1885年，巴尔末就发现氢光谱的谱线波长值是具有一定规律的，经过大量计算，他得出了下面的公式：

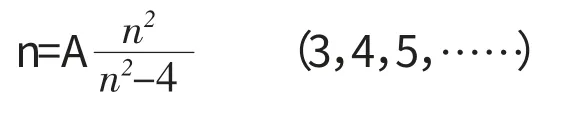
即巴尔末公式，与之相对应的那组谱线则被称为巴尔末线系[1]。几年之后，里德伯又得到里德伯常数RH=4/A，使巴尔末公式得到简化。后来，又相继发现了氢原子光谱的其它谱线系，如莱曼系、帕邢系等。

1913年，以巴尔末公式为基础，玻尔对光谱作了一个总结。根据玻尔理论，求得了原子能级与光谱的关系如下：

将此式与巴尔末公式作对比，便可很容易得到里德伯常量与各基本物理量之间的联系。

量子力学可以说是原子光谱理论基础的解说者。由于原子内部运动状态不同，所以它处于不同的定态。每一定态都具有一定的能量，它主要包括原子体系内部运动的动能、核与电子间的相互作用能以及电子间的相互作用能。能量最低的态叫做基态，能量高于基态的叫做激发态，它们构成原子的各能级。由量子力学可以推知氢原子的能级为：

原子光谱的不连续表明了原子的能量是量子化的，对原子光谱的研究是探索原子核外电子排布的重要手段之一[2]。

2.2 色散现象及色散器件

光的色散即复色光分解为单色光而形成光谱的现象。我们知道，同一种介质对不同波长的光折射率是不相同的。当复色光通过光栅、三棱镜等色散器件时，不同波长的光传播方向会有不同程度的偏折，因而在通过色散器件后就被分散开来，形成光谱。

1936年柯西研究了材料在可见光区的折射率，将色散曲线表示为：

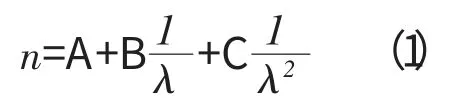
此式称为柯西公式，式中的A、B、C是表征材料特征的常数，与材料性质有关。通常把符合这一规律的色散称为正常色散。因此，只要测出棱镜玻璃的折射率n 就可以得到谱线的波长λ。不同材料A、B、C特征常数不同，色散关系曲线也不同。即：对于同一棱镜玻璃，折射率随波长的变化曲线是恒定的。

图1 最小偏向角测量光路图

色散可通过棱镜作为色散器件来实现。棱镜的主要作用就是使光线的行进方向发生偏折，如图1所示。可以证明，棱镜玻璃的折射率n 与棱镜角α、最小偏向角δm有以下关系：

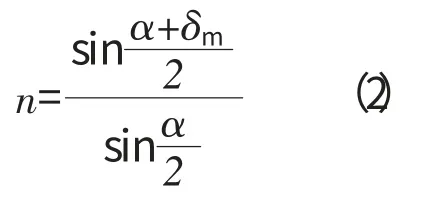
因此，只要测出α 与δm，就可以用式（2）求得棱镜玻璃的折射率n[3]150-155。

3 原子光谱的实验研究

在近代物理实验中，一般用棱镜摄谱仪或光栅摄谱仪进行原子光谱的实验研究，而本文则是用最简单的实验仪器分光计对原子光谱作定性研究，用已知的汞灯谱线的波长与折射率所拟合的色散关系来推知氦灯、氖灯的各条谱线的波长。

3.1 最小偏向角和折射率测量

如图1所示，出射光线与入射光线之间的夹角称为三棱镜的偏向角，当入射角等于出射角时，偏向角有最小值，称为最小偏向角。以汞灯作为光源，观察到光的色散现象，调节出清晰的光谱，将汞灯所发出的光谱谱线的波长值作为已知，测出汞光谱各条谱线的最小偏向角，再由(2)式计算出棱镜玻璃相对于不同波长光的折射率（如表1所示数据）。

表1 汞光谱的最小偏向角和折射率

用同一块三棱镜，以同样的方法，分别测得氦光谱和氖光谱各条谱线的最小偏向角和棱镜玻璃对应于各条谱线波长的折射率，见表2和表3所示数据。

表2 氦光谱的最小偏向角和折射率

表3 氖光谱的最小偏向角和折射率

3.2 拟合经验公式

实验测出了棱镜玻璃相对于汞光谱不同颜色（不同波长）光的折射率，如表4所示的汞光谱波长与折射率关系数据。

表4 n～λ 关系数据表

由表4中的数据，用Origin计算软件绘制出关系曲线，即：色散定标曲线（如图2所示）。并由实验实测数据拟合折射率n 与波长λ 关系的经验公式如下：

即棱镜玻璃的色散经验公式。

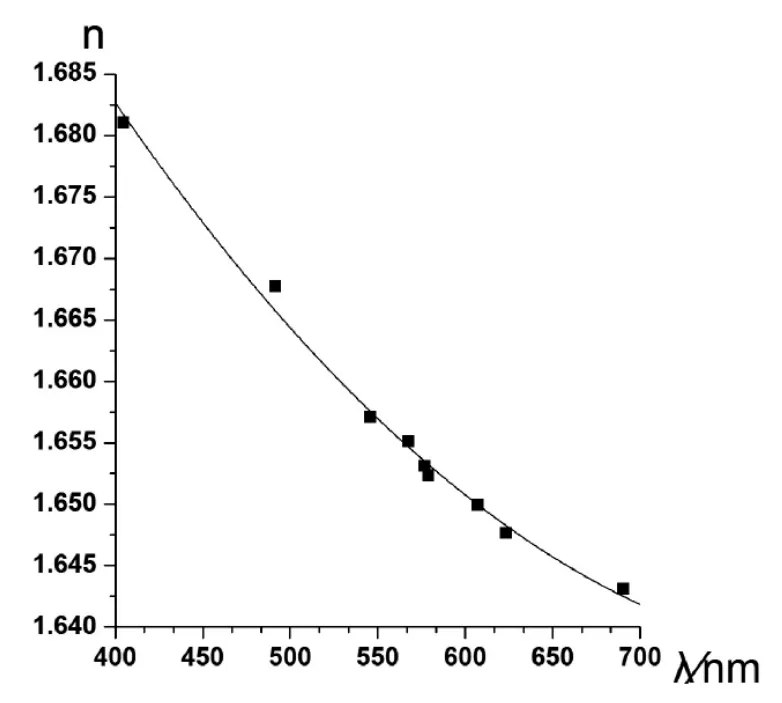
图2 棱镜玻璃色散曲线

3.3 氦光谱、氖光谱各条谱线波长的确定

公式（3）是以汞光谱为标准谱线而拟合的棱镜玻璃的色散关系经验公式。由于同一玻璃棱镜的色散关系相同，因此，实验所测得的氦光谱和氖光谱不同颜色光的折射率也同样满足色散经验公式，即通过色散经验公式可得到氦光谱与氖光谱谱线的波长。如表5与表6的数据。

表5 氦光谱的折射率和波长

表6 氖光谱的折射率和波长

4 结果与分析

⑴由表1到表6的数据以及图2的色散定标曲线可知，红光折射率最小，而紫光折射率最大，表现为玻璃介质的折射率随光波长的增大而减小，其色散曲线n～λ 呈单调下降，是正常色散。即：折射率的大小随最小偏向角的增大而增大，随波长的增大而减小。

⑵图2的色散定标曲线表明：实验测得数据基本分布在曲线上或曲线两侧。由实验结果可知，在可见光范围内，波长的实测值与文献值十分接近，而且，随着波长的逐渐增大，实测值与文献值的吻合度就越高。

⑶将棱镜玻璃的色散经验公式与柯西公式比较，其特征常数为：A=1.5725，B=53.204，C=3.6794×103。由色散经验公式可得到：8条氦光谱谱线的波长与科技文献中所公布的波长值相比对基本相符，还测出了波长值为633.6 nm、629.6 nm、612.0 nm、415.0 nm等相对强度极微弱的、相关文献未公布的4条氦光谱谱线的波长以及3条文献未公布的波长值为511.0 nm、508.3 nm、485.3 nm的氖光谱谱线波长。也就是说，由于汞灯谱线数量有限，难以覆盖全范围谱线折射率，借助色散经验公式可得到其他任意谱线的折射率，尤其是汞灯的F 和C 谱线的折射率，从而计算得到玻璃材料的中部色散。

5 结论

通过用普通物理实验室最常用的实验仪器分光计与色散器件三棱镜观察了汞灯、氦灯与氖灯的原子光谱，并用最小偏向角法测得了棱镜玻璃相对于不同颜色（不同波长）光的折射率，用已知的汞灯谱线波长与实测的折射率拟合出了棱镜玻璃色散定标曲线，由棱镜玻璃的色散经验公式确定了未知波长，即氦灯、氖灯各条谱线的波长，特别是氦光谱中部分相对强度极微弱、而且文献资料中未公布的谱线波长。实验结果表明：用普通的光学色散器件研究原子光谱，虽然测量仪器与色散器件只能测出有限条谱线的折射率，但拟合的色散经验公式意义重大。这样，不但丰富了基础物理实验的内容、拓宽了基础物理实验途径，而且为近代物理实验的开设，以及使用单色仪、摄谱仪等精密的光学实验仪器与光谱分析技术奠定了一定的实验基础。

［1］贾翠红,林锦.氢原子光谱实验的误差及其优化问题研究［J］.大学物理实验,2011,24(5):95-96.

［2］刘绒侠.利用色散法探索玻尔氢原子理论测量普朗克常数［J］.物理实验,2008,21(3):4-7.

［3］王铁云.大学物理实验教程［M］.北京:北京师范大学出版社,2011,150-155.