用3Dmax证明立方密积结构为面心立方

马厂

摘 要 利用3Dmax软件实现晶体的立方密堆积并生成模型，并通过各种旋转操作，找出了模型中的面心立方晶胞，从而证明了立方密积结构为面心立方，加深了对密堆积的理解。

关键词 密堆积；立方密积；晶胞

一、引言

密堆积晶体结构模型在物理和化学中应用的比较广泛。通过密堆积我们可以研究金属晶体和离子晶体的结构。但是密堆积的结构比较依赖空间想象力，而证明立方密积结构为面心立方更是固体物理教学中的一个难点，所以3Dmax来实现人眼的视觉感知效果成为了一个重要课题。3Dmax综合了测量学、艺术学、计算机等学科的技术，是用来制作动画以及模型的最佳软件，用它来制作晶体的密堆积事倍功半，还可以360度无死角观察模型的各个角落。利用3Dmax实现晶体的密堆积并生成模型，通过各种组合，加深对密堆积的理解。

二、立方密积

如果晶体由完全相同的一种粒子组成，而粒子被看作小圆球，则这些全同的小圆球最紧密的堆积称为密堆积。立方密积是密堆积结构的两种基本型式之一，其圆球的配位数为12，空间利用率为74.05%，密置层按三层重复，即ABC ABC……的方式重复堆积，其第四层的球心投影位置与第一层重复，第五层与第二层重复，依此类推，如图1所示。由于在这种堆积中可以划分出立方面心格子，故称为立方最紧密堆积，其密置层平行于{111}。 三、用3Dmax软件生成模型

1.A层的生成

先设定中心红球的大小及位置。其他等大六球均与它相切，可分别计算坐标并生成，如图1所示。

2.B层的生成

B层圆球均要落入A层中的空隙，可将A层圆球进行复制并往XYZ各轴进行适当的平移，如图2所示。此过程可进行多视角切换，以确保B层圆球位置的精确性。

3.C层及第四层的生成

C层及第四层的生成方式与B层生成方式相同，如图3、图4所示。注意第四层也为A层，即第四层与A层的区别仅仅是Z轴方向的坐标不同。

4.从模型中找出面心立方晶胞

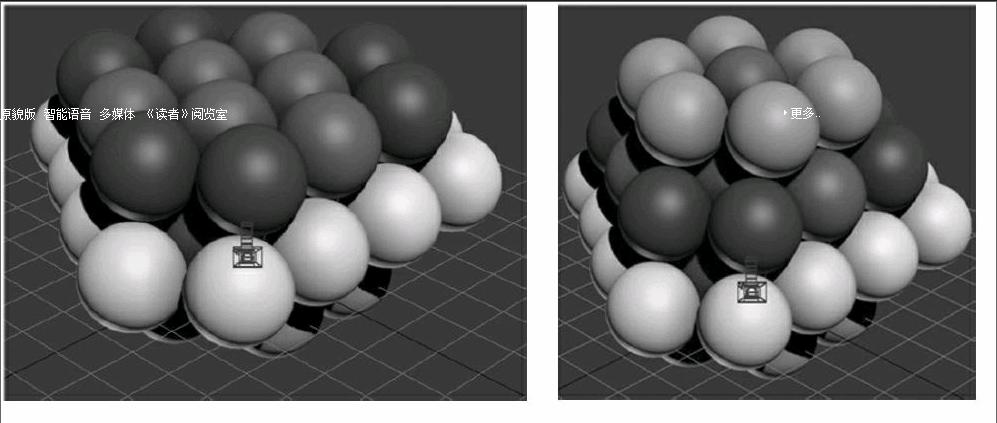
从图4模型中找出与面心立方晶胞相关的14个圆球，此前已经标记为红色，去掉其他圆球即可，如图5所示。并通过软件的旋转操作将模型平放，并与标准的面心立方结构进行比较，如图6所示。

四、结论

介绍了如何利用3Dmax软件制作立方密积结构模型。可以旋转模型从不同的角度观察各个球在空间中的位置关系，从而证明了立方密积结构为面心立方，加深了对于密堆积的理解。3Dmax软件使抽象的内容形象化，静止的内容动感化，将较难以解决的问题用计算机模拟实验的空间加深了对知识的理解。

参考文献：

[1]裴冬冬.基于JAVA3D的晶体结构模型研究[J].微型机与应用，2007，11：32-34.

[2]北京师范大学，华中师范大学，南京师范大学无机化学教研室合编.无机化学（下册）[M].北京：高等教育出版社，2003：928-929.

[3]朱万强，牟青松.高中化学教学中晶体密堆积结构的空隙排布[J].遵义师范学院学报，2009，11（3）：98-101.endprint