增强模型理解 提炼一般方法——由一道求配位数高考题引发的思考

吴 迪

(广东省深圳市深圳科学高中)

高中阶段,配位数一般是指离子晶体中每个离子附近的最近的其他异号离子数,或者金属晶体/共价晶体/分子晶体中,距离每个原子(或分子)最近的其他原子(或分子)数。在晶胞学习中,配位数可用于定量地描述晶体晶胞的结构,有助于深入认识离子晶体晶胞结构和离子半径比的关系(如氯化钠和氯化铯),共价晶体晶胞结构和原子价层电子对数的关系(如金刚石和二氧化硅),分子晶体晶胞结构和氢键方向性、范德华力的无方向性的关系(如冰和干冰)等。而配位数的求算对学生的空间想象能力要求较高,晶体晶胞的结构种类繁多,学生求算时往往会出现因未注意其他相邻晶胞中也存在符合配位数计算要求的对象而漏算或因计数对象被不同晶胞共用重复计数而多算等情况,导致不能准确判断。因此,配位数求算往往是学生学习中的难点。对晶体相关的基础计算问题,基于典型晶体模型的充分理解可快速求解;但对于较为复杂的晶胞,常规的晶胞模型已经不能直接迁移,需要对晶体模型进行深入理解并探究一般方法。笔者基于对2023年6月浙江卷的一道高考题的思考,介绍解决配位数计算问题的思维推导过程,并形成求算配位数的一般方法,进一步深入理解概念和模型在解决化学问题时的重要作用。

一、配位数计算试题分析

2023年高考落下帷幕,其中浙江卷17(3)题包含求配位数的一问:某含氮化合物晶胞如图1所示,每个阴离子团的配位数(紧邻的阳离子数)为________。

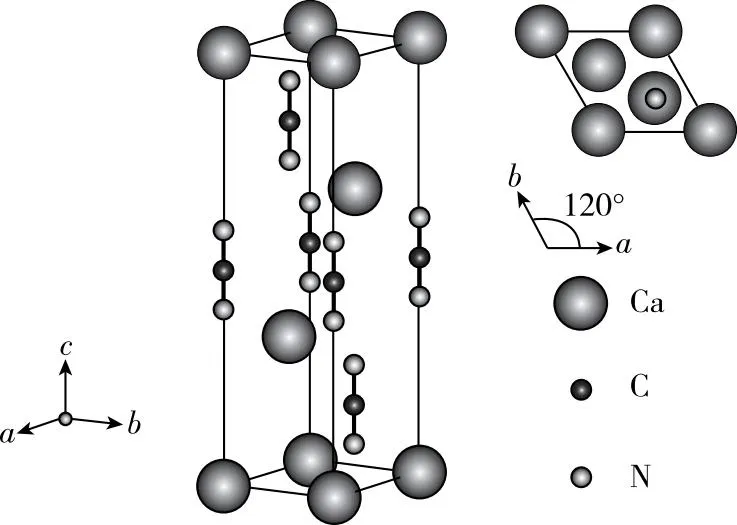
图1 2023年6月浙江卷17题图

该晶体(CaCN2)晶胞为六方晶胞,对各离子的编号如图2所示,如果观察晶胞内部最上方的阴离子团①号,很容易看出在晶胞中表示出来的钙离子中,有4个离它最近(位于顶点的a、b、d和内部的e),但其实该阴离子团的配位数为6,还有两个离它最近的钙离子位于相邻晶胞的内部,很容易被忽略,需要拓展画出附近晶胞才能正确解答。

图2 晶胞离子编号图

二、配位数求算一般方法思维推导过程

晶胞是表征晶体结构的基本单位,理论上,一个晶胞就可以反映晶体的所有信息,能不能仅通过观察一个晶胞就计算出配位数呢?

(一)晶胞模型理解一:求某原子的配位数相当于把该原子与配位原子连线,求这些连线中最短线段的个数

要比较方便地计算晶胞的配位数,首先需要深入理解配位数的概念,将其与我们熟悉的知识和技巧联系起来。配位数是距离某一个原子(离子)最近的其他原子(离子)的个数(此处仅以原子为例,离子或原子团也适用),实际上求配位数时,经常比较的是各原子与该原子连线的线段长度,其中最短线段对应的即为与其配位的原子,因为每两个原子之间有且只有一条连线,这个最短线段的个数就是配位数。这样,我们就可以在晶胞中画出这些连线,从而使得配位数的求算转化为判断最短线段的个数。如图3中,对于阴离子团⑤,画出其与各个方向上最近的钙离子连线,其中与e、f的连线最短(图中黑色实线)计入配位数,与d、k的连线(图中黑色虚线)较长不计入。

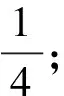
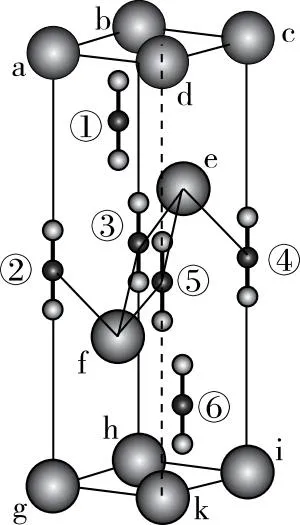
图3 晶胞离子连线图

(二)晶胞模型理解二:对于晶胞相互平行的棱上的四个可以通过晶胞平移密铺互相重合的点,它们在本晶胞内与其他点的相对位置,反映了其中一个点分别在共用它的四个晶胞中和其他点的相对位置

在浙江卷这道高考题中,观察图1晶胞中层的四个阴离子团,根据晶胞的无限重复平移、无隙拼接的特性,它们各自在本晶胞中的环境(其他原子和它的相对位置)其实相当于某一个阴离子团在共用它的四个晶胞中的环境。因此,我们可以分别将这四个阴离子团(即图3中的②、③、④、⑤)与最近的阳离子连线,最短连线的个数分别为1个、2个、1个和2个(如图3中黑色实线所示),且这些连线均在晶胞内部,其个数加和即为距离每个阴离子团(在共用它的四个晶胞中)最近的阳离子个数,也就是配位数为6,实现了仅观察一个晶胞就可以计算配位数的目标。

解决该具体问题之后,下一步就是思考能不能由特殊推广到一般,也就是如果求配位数的原子在棱上,是不是一定能仅观察一个晶胞内部就计算出距离该原子最近的某种原子数呢?笔者进行了一些常见晶胞的验算。

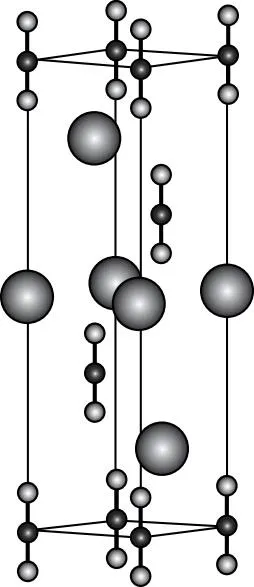
图4 晶体的另一种晶胞

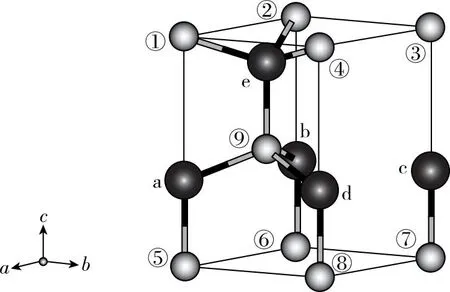
图5 六方硫化锌晶胞示意图

(三)晶胞模型理解三:晶胞的八个顶点在本晶胞内和其他点的相对位置,反映了其中一个点分别在共用它的八个晶胞内和其他点的相对位置

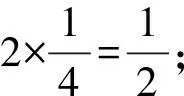
为什么对于同一个晶胞,研究的中心点为晶胞顶点、晶胞棱上的点和晶胞内部的点时,只考虑该晶胞内部的计算正确率不同呢?这是因为对于晶胞内部的点,该晶胞只能体现其在该晶胞范围内的环境(其他点和它的相对位置);而对于晶胞棱上的点,如果考虑互相平行的棱上的四个对应的点(能在晶胞平移密铺中重合的点)在本晶胞范围内的环境,即等价于考虑其中一个点在其共用的四个晶胞范围内的环境,我们实际考查的晶体结构范围就扩大到了四个晶胞,对配位原子的筛选范围更大。同理,如果考虑8个顶点在本晶胞内的环境,即等价于考虑其中一个点在其共用的8个晶胞范围内的环境,实际考查的晶体结构范围就扩大到了8个晶胞,对配位原子的筛选也就包括了8个晶胞的范围,更全面了。

那么,是不是研究的中心点为晶胞顶点时,用该方法一定能计算正确呢?答案是肯定的,因为距离顶点最近的原子必然会出现在共用该顶点的8个晶胞内,在研究8个顶点时就全部覆盖到了。

用反证法证明如下:假设存在一个点P上的W原子,它距离某个晶胞顶点O最近但却不在共用该晶胞顶点的8个晶胞内。设该晶胞三条棱长分别为a、b、c,选取该晶胞顶点O为坐标原点(0,0,0),沿着晶胞的三条棱选取坐标轴,选择合适的坐标系方向,可使点P位于第一象限或第一象限相邻坐标轴和坐标面上,即若其坐标为P(x,y,z),则x、y、z均不小于0。由于其不在距离原点最近的晶胞内,则x≥a,y≥b,z≥c至少有一项成立且不能都相等。若x≥a成立,则点Q(x-a,y,z)距离原点O比P更近,根据晶胞无隙平移密铺的特性,若P点存在W原子,则Q点也存在W原子,因此P点处的W原子必然不是距离晶胞顶点O最近的W原子;若y≥b或z≥c,同理可找到比P点距离顶点O最近的W原子,与假设矛盾,原结论成立。

因此,用单一晶胞计算配位数时,应优先选取晶胞上8个顶点为研究对象,若想研究的原子或离子不在顶点上,则需进行选取晶胞范围的平移,重新选取晶胞使其在顶点再进行研究才能确保计算结果正确。

由此笔者得到更科学的研究图1晶胞的方法是,将晶胞坐标系原点沿c轴方向平移到阴离子团的中心,此时构造的晶胞如图4所示,和原晶胞图1的区别是阳离子和阴离子团互相对调位置,再进行计算。简便起见,对于仅有一种阴离子和一种阳离子构成的晶胞,也可先计算其中一种的配位数,另一种根据配位数之比等于单个离子所带电荷数之比来换算。如对于图1所示CaCN2晶胞,可先根据顶点的钙离子计算出钙离子的配位数为6(棱上的阴离子团距离顶点比内部的阴离子团距离顶点远),由其分子式CaCN2,推算出阴离子团的配位数也为6。

三、配位数求算的一般方法及应用

(一)计算配位数(相邻最近的某类原子数)的一般方法

第一步,平移晶胞,使得待研究配位数的粒子位于晶胞顶点。

若仅由一种阴离子和一种阳离子构成的晶胞,也可先计算其中在顶点的那种离子的配位数,另一种的配位数根据配位数之比等于单个离子所带电荷数之比换算。

(二)应用该求配位数一般方法进行计算

【例1】计算立方硫化锌(如图6)中锌离子(晶胞顶点为锌离子)的配位数。

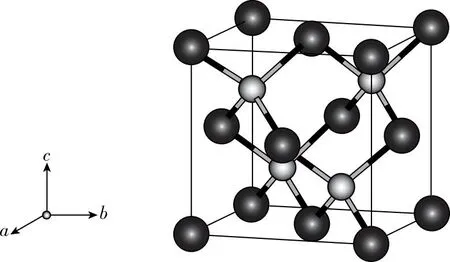
图6 立方硫化锌晶体的晶胞示意图

【解答】观察图6顶点的8个锌离子,只有4个锌离子附近都有1个硫离子连线最短,且连线在晶胞内部计1,故锌离子的配位数为1×4=4。

【例2】计算六方硫化锌(图5)中硫离子的配位数。

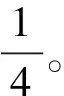
【例3】计算氟化钙晶体(如图7所示,顶点为钙离子)中钙离子和氟离子的配位数。

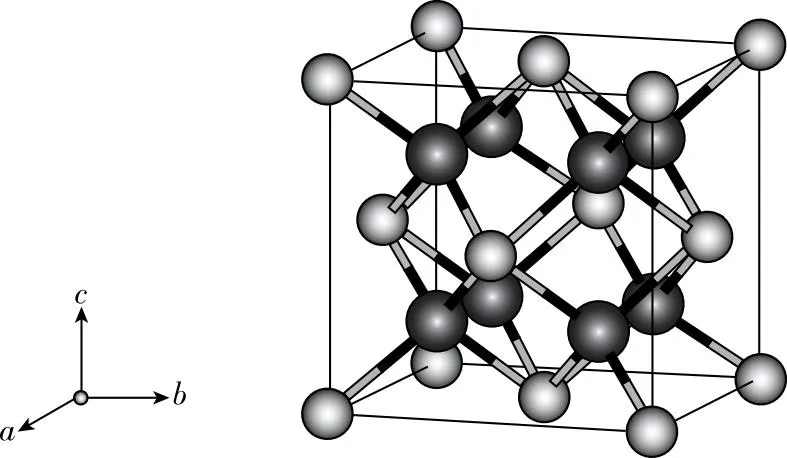
图7 氟化钙晶体的晶胞示意图

【解答】观察图7顶点的8个钙离子,每个钙离子附近都有1个氟离子连线最短,且连线在晶胞内部计1,故钙离子的配位数为1×8=8,由氟离子和钙离子的配位数之比等于电荷数之比也就是1∶2,推算出氟离子的配位数为4。

【例4】计算氯化钠晶体中钠离子的配位数和与钠离子最近的钠离子个数(如图8,其中晶胞顶点处为钠离子)。

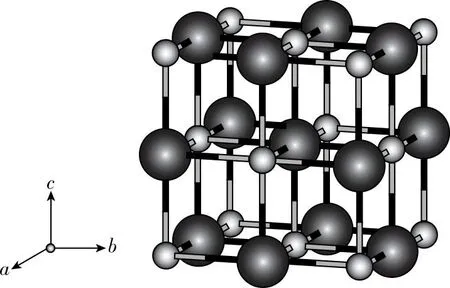
图8 氯化钠晶体的晶胞示意图

以上例子均为离子晶体晶胞,但该方法对各类晶体均适用,如对于金属晶体六方密堆积的配位数的计算和前文六方硫化锌每个硫离子最近硫离子个数的计算一致,配位数为12;立方密堆积和【例4】中与钠离子最近的钠离子个数的计算一致,配位数为12;金刚石晶体的配位数计算与【例1】锌离子配位数计算一致,配位数为4,此处不再赘述。

四、总结与思考

综上,本文所呈现出的求算配位数的一般方法主要围绕着晶胞模型的理解和认识展开,并利用晶胞的特性证明了所得到的结论。然而,随着试题情境的不断创新,学生会面临更多陌生、复杂综合的真实情境下问题的解决,方法总结也很难做到面面俱全,需要不断优化完善。因此,教师不仅要引导学生形成解决具体问题的一般方法,更要帮助学生增强学科思维,提升学生对相关模型的认识与理解,增强学生分析解决实际问题的能力,从而助力于学生学科核心素养的全面发展。