浅谈晶胞空间利用率的计算
2019-11-08 03:23
中学生数理化(高中版.高考理化) 2019年10期
人教版化学选修3《物质结构与性质》第三章第三节中提到晶胞空间利用率的问题,近几年的高考试题中也经常出现相关的计算,此类计算灵活度较高,分析方法多样,不太容易得分。笔者认为只要同学们能掌握几种常见的晶胞空间利用率的计算,基本上就能突破这一难点。下面就常见的金属晶胞和金刚石晶胞空间利用率的计算做一分析,以供同学们参考。

1.简单立方堆积(如图1所示):金属原子位于晶胞的八个顶点上,相邻的两个原子相切,设原子的半径为r,晶胞的边长为a(下同),则a=2r,每个晶胞中净含有一个金属原子。
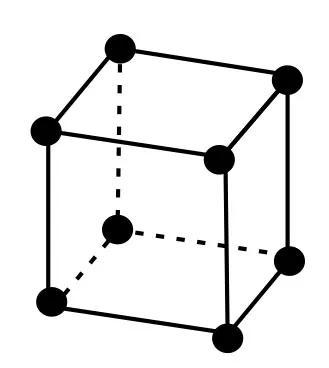
图1
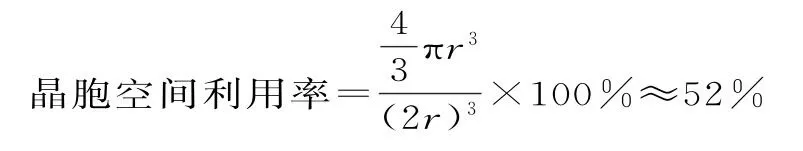
2.体心立方堆积(如图2所示):此种堆积方式可看成简单立方堆积模型中心再排一个金属原子,a>2r,晶胞的体对角线的长等于4r,则得每个晶胞中净含有两个金属原子。
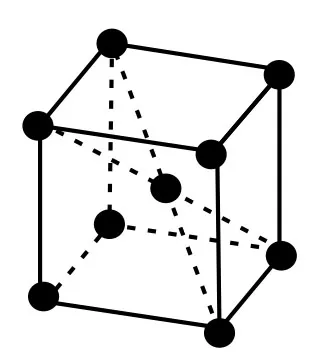
图2

3.面心立方最密堆积(如图3所示):金属原子位于晶胞的顶点和面心上,平均每个晶胞中净含有四个金属原子,且面对角线的长为4r,则a2+a2=(4r)2,得
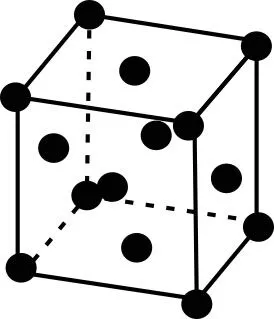
图3

4.六方最密堆积(如图4甲所示):晶胞的上下面是菱形,菱形顶点上相邻的原子两两相切,短对角线上两个原子也是相切的。若沿上下面短对角线方向切开,则形成两个正三棱柱,其中一个正三棱柱的正中心有一个金属原子,如图4乙所示,另一个则没有。图4乙中正中心的原子与上下面的原子形成两个正四面体,每一个正四面体如图4丙所示(放大后,BF=2FE,则AF2=得晶胞的体积=S菱形×
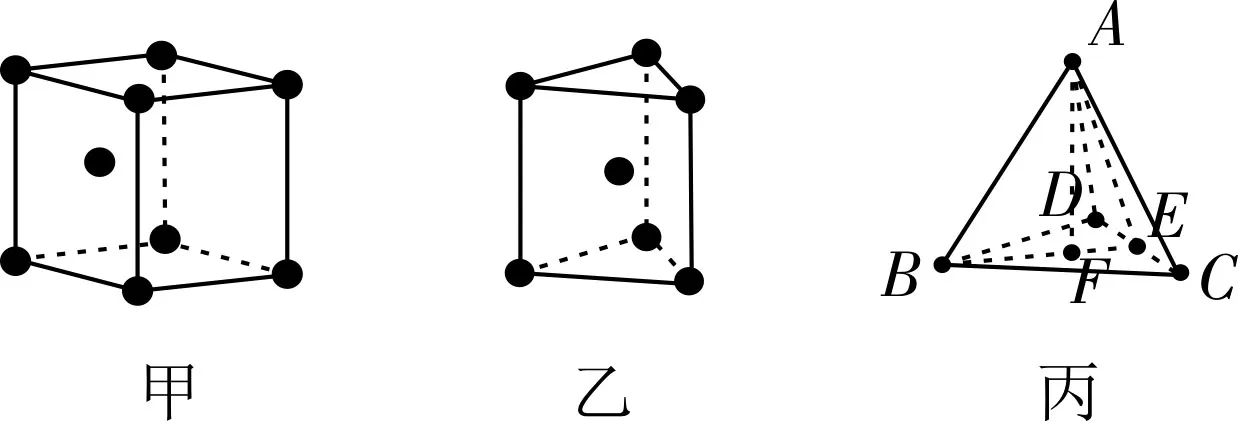
图4

5.金刚石晶胞(如图5所示):每个晶胞中净含有8个碳原子,体对角线的长为8r,则得
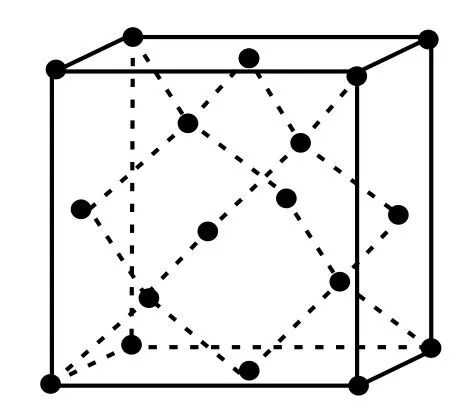
图5

同学们若能熟练掌握以上几种常见的晶胞空间利用率的计算,则其他类型的晶胞空间利用率的计算也就迎刃而解了。
猜你喜欢
考试与评价·高二版(2020年6期)2020-09-10
新高考·高一数学(2019年3期)2019-09-07
高中生学习·高二版(2016年8期)2016-05-14
中学生数理化·八年级数学人教版(2016年2期)2016-04-13
中学生数理化·八年级数学人教版(2016年3期)2016-04-13
小雪花·成长指南(2015年7期)2015-08-11
小天使·五年级语数英综合(2014年12期)2015-01-14
中学数学研究(2008年8期)2008-12-09
意林(2008年12期)2008-05-14
意林(2008年14期)2008-05-14

