高中数学复习之微专题的研发与应用——高中数学解析几何复习与平面向量的融合策略

数学中的解析几何和平面向量不仅是学习中的重难点,还是在高考试卷中占重要分量的题型,但是对于大部分同学而言,解析几何复习与平面向量的融合一直是学习的难点。我们知道平面向量具有代数形式和几何形式的双重身份,是数形结合的典范。所以,在复习解析几何时将其与平面向量进行融合,会收到很好的学习效果。

一、高中数学解析几何的重要性

在高中数学的整个内容中,解析几何这部分内容占据了非常重要的分量。这部分知识对于计算能力和思维能力有很好的培养作用。第一,解析几何具有承上启下的作用,这部分内容不仅可以补充初中时期平面几何的不足,还可以为以后更深层次的学习打下坚实的基础【1】。第二,在高中数学所有的知识点内,解析几何这部分的内容具有交叉的作用。这部分内容能够将已经学习过的平面向量和代数知识进行结合。所以,如果对于这部分知识理解不够透彻,就会导致在学习解析几何的时候有一定的障碍。在学习和掌握解析几何的时候,需要灵活地运用,以此来提升自身的学习水平。第三,解析几何部分注重的是方法论,它的特点是非常抽象,同时系统性非常强,并且知识体系也较为完善,所以,在解析几何的学习过程中,可以增强对于其他学科的应用能力【2】。

二、解析几何复习与平面向量的融合策略

(一)与数乘向量的融合

向量在数形结合中起到桥梁的作用,通过向量可将解析几何中的运算问题转化成坐标运算,所以数乘向量与解析几何的融合问题是近年来大家广泛关注的一个问题。

例1在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边所围成的区域(含边界)上。

解：(1)方法1：因为又因为=(1-x,1-y)+(2-x,3-y)+(3-x,2-y)=(6-3x,6-3y),所以(2,2),故

令y-x=t,那么由图1所示,当直线y=x+t过点B(2,3)时,t取得最大值为1,所以m-n的最大值也为1。

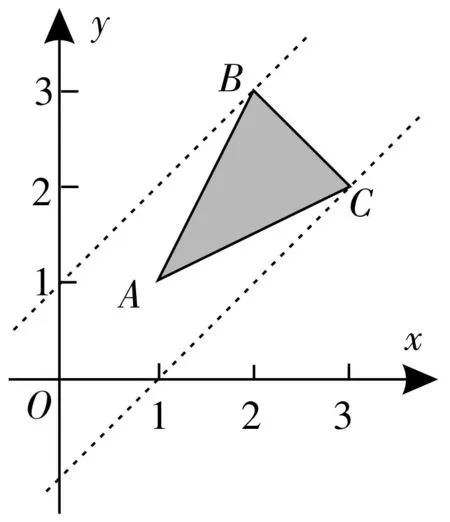
图1

评析：这道题考查了向量知识与线性规划的融合。利用数乘向量的知识,可将解析几何的问题转化成向量坐标的运算问题,简化解题过程。

(二)与共线向量的融合

由于向量具有数形结合融为一体的特点,所以常常会成为高中数学知识的一个交集点,平面向量与解析几何的融合是高三同学需要复习的重点内容,因为这种类型的题目已发展成为高考命题的热点,特别是共线向量与解析几何的融合更是近年来高考的热点题型。

例2已知抛物线C：y2=4x的焦点是F。

(1)点A,P满足当点A在抛物线C上运动时,求动点P的轨迹方程。

(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果这种情况存在,请求出所有可以满足条件的点Q的坐标；如果这种情况不存在,请说明理由。

分析：可以确认这是一道直线与圆锥曲线位置关系的题目。首先,应该根据题目的条件设出向量以及；然后,利用共线向量求出动点P的轨迹方程；最后,根据点Q关于直线y=2x对称点的条件,求出点Q的坐标。

解：(1)设P(x,y),A(xA,yA),则(x-xA,y-yA)。因为F(1,0),因此(xA-1,yA),由可得(x-xA,y-yA)=-2(xA-1,yA),即解得代入y2=4x,从而得到动点P的轨迹方程为y2=8-4x。

(2)设点Q为(t,0),则点Q关于直线y=2x的对称点为Q′(x,y),所以：

若点Q′在C上,将点Q′的坐标代入y2=4x,得出4t2+15t=0,即t=0或

所以满足题意的点Q是存在的,并且它的坐标为(0,0)和

评析：这道题目通过交汇融合共线向量与解析几何,变成了一道探求点P的轨迹方程问题,并在此基础上变成了探求点Q是否真实存在的一道具有综合性特点的问题。这道题目既考查了平面向量的运算和概念,也考查了关于解析几何中的圆锥曲线和直线问题的解题水平。

三、掌握复习方法,提升学习兴趣

解析几何近年来已成为高考的重点,对于解析几何的复习也是困扰同学们的一个难题。因此,掌握解析几何的解题方法才是学习的重中之重,而解答解析几何问题的主要方法就是数形结合法。希望同学们都要自己探索解题方法,增强探究能力,提升解题的能力。