高考数列题的分析与解题策略
在近几年的高考中,虽然对数列题目的考核比较灵活,但一些常考的题型也会反复出现在高考中。因此,掌握数列题目的重点题型及解题策略,对掌握数列知识和提高数列解题能力有重要意义。下面对几个常考、重点题型及其解题策略进行分析。
一、求数列通项公式
数列的通项公式是研究数列的重要内容之一,也是每年高考数列题目中出现和应用最多的题型。
例1若数列{an}的前n项和是Sn,并且2Sn=3n+3,求数列{an}的通项公式。
解析:根据2Sn=3n+3可以得出2Sn-1=3n-1+3(n≥2),两个式子相减,得an=3n-1。因为2a1=3+3,可求出a1=3,因此可求出数列{an}的通项是an=
策略:解答本题利用了Sn和an之间的关系,求解通项时需要验证首项。在近几年的高考中用公式法求通项的题占大部分,其次是用Sn和an之间的关系求通项,而其他方法用得较少。许多数列问题需要将递推关系变形,再利用相应方法求通项。
二、求数列前n项和
例2已知一个数列{an}满足条件an+2=qan(q为实数,并且q≠1),n∈N*,a1=1,a2=2,并且a2+a3,a3+a4,a4+a5成等差数列。(1)求q的值和数列{an}的通项公式。(2)假如求数列{bn}的前n项和Sn。
解析:(1)可求得q=2,{an}的通项是
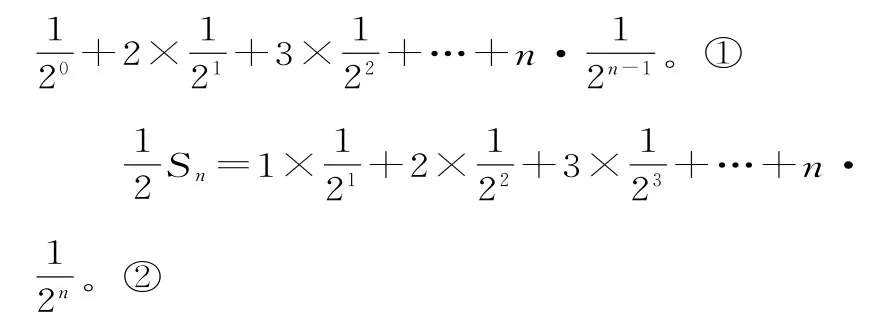
策略:求数列{bn}的前n项和Sn时,根据通项公式特点,可运用错位相减的方法求出前n项和。从近几年各地的考题看,运用错位相减法、公式法、裂项相消法解题的类型较多。
三、证明数列不等式
例3已知数列{an}满足条件并且证明:1≤
证明:根据题意可得an+1-an=-≤0,也就是an+1≤an,因此可得出本数列是递减数列。因为,所以,根据an+1=an-a2n可得出an=(1-an-1)an-1,an=(1-an-1)·(1-an-2)…(1-a1)a1>0。因为可得出由此得出N*)成立。
策略:本题通过递推式变形后可判断出是递减数列,因而能确定数列的最大项就是其首项,确定数列的取值范围是其证明重点。在本题的证明中,运用了数列的单调性来证明不等式成立,此方法的证明策略为:一是直接证明数列的单调性,确定最值后方便证明;二是构建一个新数列,来证明新数列的单调性,求出新数列的最值后求证不等式成立。

