典型晶体微粒组成及晶胞参数计算常见考点例析
王 春
(北京教育学院)
晶体的微粒组成与晶胞参数的计算是近年来全国高校自主招生考试和高考试题中考查的热点内容,试题侧重考查学生的观察能力和三维空间想象能力,将立体几何知识与化学知识紧密结合在一起.试题的难度较大,试题考查的内容主要涉及晶胞的微粒组成、晶胞的密度、微粒间的距离、空间占有率的相关计算、原子分数坐标的确定等内容.本文就晶胞的微粒组成与晶胞参数的计算常见考点,结合典型例题进行分类介绍,以供广大考生进行考前复习参考.
1 晶胞中微粒数目及晶体化学式的计算
对于晶胞中微粒数目的计算,一般采取的方法为“均摊法”,该方法的原则是晶胞中任意位置上的1个原子如果是被n个晶胞所共有,那么,每个晶胞对这个原子分得的份额就是.对于长方体(包括立方体)晶胞中不同位置的微粒数的计算方法如图1所示.
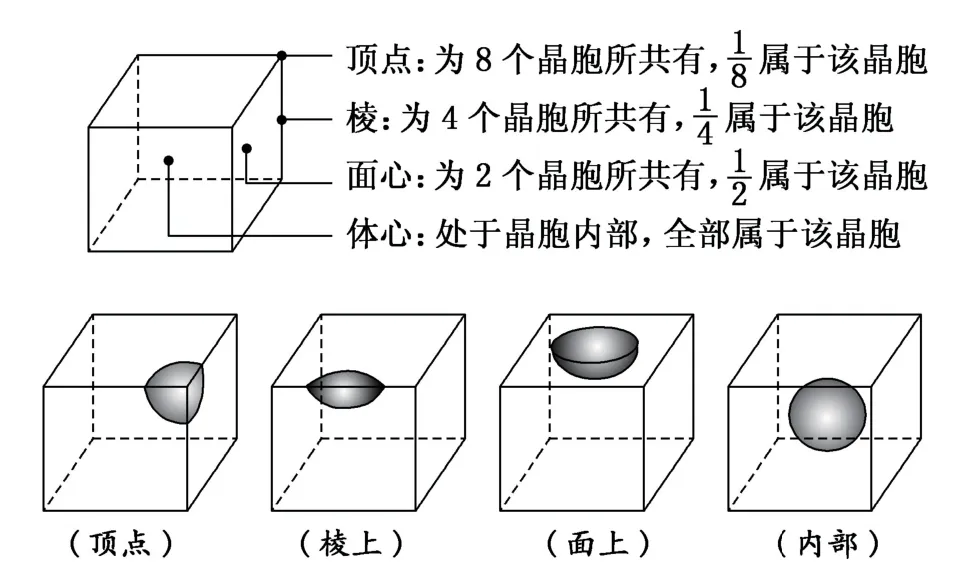
图1
对于非平行六面体形晶胞中微粒数目的计算同样可用“均摊法”,其关键仍是确定1个微粒为几个晶胞所共有.例如,石墨晶胞(如图2)中每一层内碳原子排成六边形,其顶点(1个碳原子)对六边形的贡献为,那么1个六边形实际有个碳原子.

图2
又如在六棱柱晶胞(MgB2,如图3)中,顶点上原子为6个晶胞(同层3个,上层或下层3个)共有,面上的原子为2个晶胞共有,因此镁原子个数为12×,硼原子个数为6.

图3
对于晶体化学式的计算可以先运用“均摊法”计算出1个晶胞中的微粒数目,求出不同粒子数目的比值,最后推求出该晶体的化学式.
例1(强基模拟题)某FexNy的晶胞如图4-甲所示,Cu可以完全替代该晶体中a位置Fe或者b位置Fe,形成Cu 替代型产物Fe(x-n)CunNy.FexNy转化为2种Cu替代型产物的能量变化如图4-乙所示,其中更稳定的Cu替代型产物的化学式为_________.

图4

根据能量越低越稳定原理,由图4-乙知,Cu替代a位置Fe型晶胞更稳定,其晶胞中Cu位于8 个顶点,,Fe 位于面心,,N 位于体心,N(N)=1,其化学式为Fe3CuN.
2 晶胞中粒子分数坐标的计算
对于晶胞中粒子分数坐标的确定,较为实用的方法是掌握几类典型的晶体模型粒子坐标及其对应的投影图,然后根据具体的晶胞特点确定粒子的坐标分数.常见的晶体模型粒子坐标及投影图如表1所示.

表1
例2(强基模拟题)原子坐标参数可以很好地表示晶胞内部各原子的相对位置,图5为Ge单晶的晶胞,其中原子坐标参数A为(0,0,0);B为();C为(,0).则D原子的坐标参数为_______.

图5

观察试题中Ge单晶的晶胞图示可知D与周围4个原子形成正四面体结构,D与顶点A的连线处于晶胞体对角线上,过面心B、C及上底面面心原子的平面且平行侧面将晶胞2等分,同理过D原子且平行侧面的平面将半个晶胞再2等分,可知D处于到各个面的处,则D原子的坐标参数为).
例3(强基模拟题)AlP因杀虫效率高、廉价易得而被广泛应用.已知AlP 的晶胞结构和A、B点的原子坐标如图6所示,则C点的原子坐标为______.

图6

观察AlP的晶胞结构可知A,B点的原子坐标分别为(0,0,0),,可知晶胞边长为1,由此可推知C点的原子坐标为.
3 晶体密度的计算
对于晶体密度的计算步骤通常为首先根据“均摊法”计算出每个晶胞中实际含有各类原子的个数,确定物质的化学式,再进一步计算出晶胞的质量,然后计算出整个晶胞的体积,最后依据密度计算公式求出晶体的密度.其中主要利用如下等式进行相关数据计算(以立方晶胞为例):a3ρNA=nM(a:棱长,ρ:密度,NA:阿伏加德罗常数的值,n:1mol晶胞所含基本粒子或特定组合的物质的量,M:组成物质的摩尔质量).注:若是长方体,V晶胞=abc,若是六棱柱,V晶胞=S底×h.
例4(强基模拟题)图7-甲是结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu.图7-乙是沿立方格子对角面取得的截图.设阿伏加德罗常数的值为NA,则MgCu2的密度是_________g·cm-3(列的拉维斯出计算表达式).

图7

例5(强基模拟题)Li2O 具有反萤石结构,晶胞如图8所示.已知晶胞参数为0.4665nm,阿伏加德罗常数的值为NA,则Li2O 的密度为_________g·cm-3(列出计算式).

图8

由题干所给图示可知,Li位于晶胞内部,O位于顶点和面心,因此1个晶胞有8个Li,O原子个数为.因此1个Li2O 晶胞的质量为,1个晶胞的体积为(0.4665×10-7)3cm3,即该晶体密度为
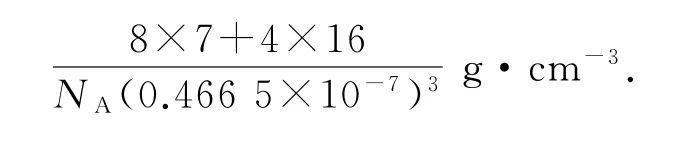
4 晶体空间利用率的计算
空间利用率是指构成晶体的原子、离子或分子在整个晶体空间中所占有的体积百分比.其具体的计算公式为:空间利用率=.其中需要掌握以下几种典型的金属晶体的空间利用率.
1)简单立方堆积(如图9)

图9
设原子半径为r,由于原子在晶胞棱的方向上相切,可以计算出晶胞参数:a=b=c=2r,α=β=γ=90°.每个晶胞中包含1个原子.
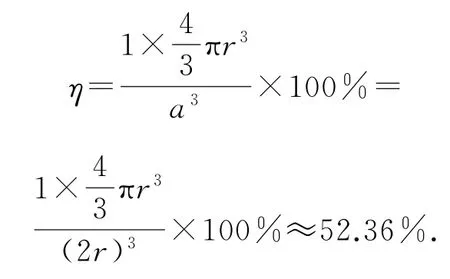
2)体心立方堆积(如图10)
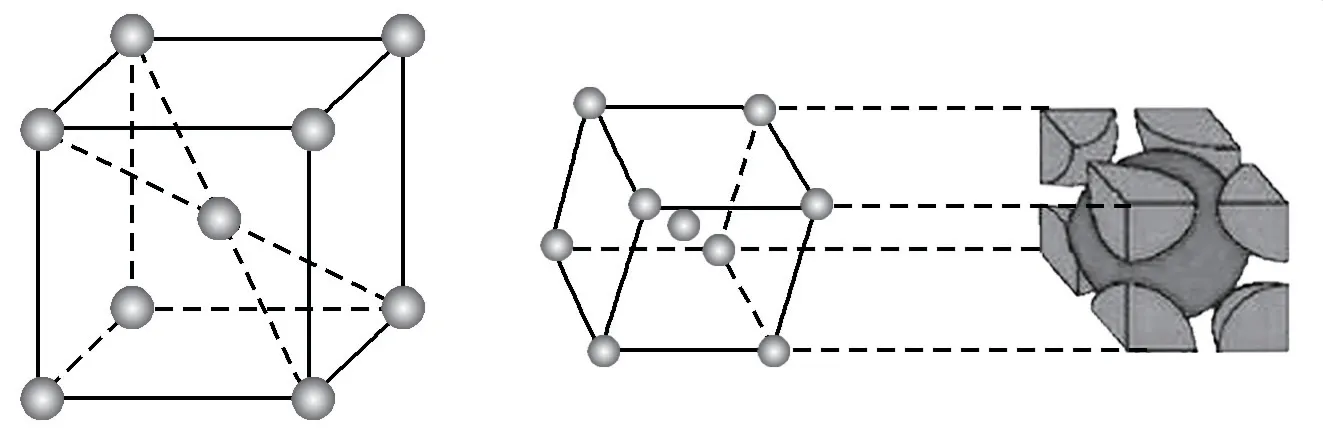
图10
设原子半径为r,由于原子在晶胞体对角线方向上相切,可以计算出晶胞参数:,α=β=γ=90°.每个晶胞中包含2个原子.

3)面心立方最密堆积(如图11)

图11
设原子半径为r,由于原子在晶胞面对角线方向上相切,可以计算出晶胞参数:,α=β=γ=90°.每个晶胞中包含4个原子.

例6(强基模拟题)钛晶体有2种晶胞,如图12所示.
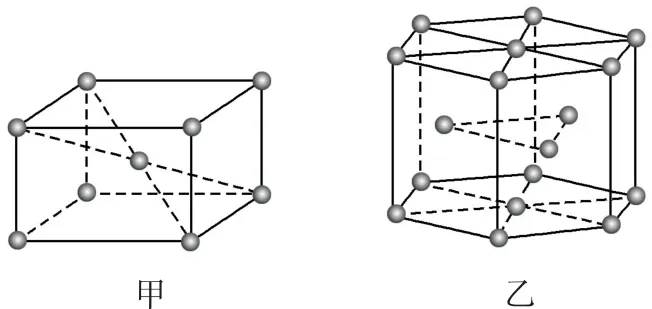
图12
(1)如图12-甲所示,晶胞的空间利用率为_________(用含π的式子表示).
(2)已知图12-乙中,六棱柱边长为xcm,高为ycm.该钛晶胞密度为Dg·cm-3,则NA为_________mol-1(用含x、y和D的式子表示).

(1)设图甲晶胞中,Ti原子半径为r,晶胞边长为a.体心立方晶胞中体对角线上3个原子相切,则有,1个晶胞含2个Ti原子,则晶胞的空间利用率

(2)把图乙六棱柱当作1个晶胞,则1个晶胞中含Ti原子数为,六棱柱的底面由6个边长为xcm 的正三角形构成,1个正三角形的面积为,则六棱柱总体积cm3,密度,则
链接练习
利用新制的Cu(OH)2检验醛基时,生成红色的Cu2O,其晶胞结构如图13所示.

图13
(1)该晶胞原子坐标参数A 为(0,0,0);B 为(1,0,0);C为).则D 原子的坐标参数为________,它代表_________原子.
(2)若Cu2O 晶体的密度为dg·cm-3,Cu和O 的原子半径分别为r(Cu)pm 和r(O)pm,阿伏加德罗常数值为NA,列式表示Cu2O 晶胞中原子的空间利用率为________.
(3)FeO 晶体结构如图14所示,若该晶胞边长为bcm,则该晶体的密度为________g·cm-3(用NA表示阿伏加德罗常数的值).
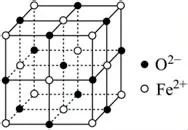
图14
链接练习参考答案

(完)

