基于支持向量机的小企业信用评级最适样本量的研究

徐旭初，高志，赵纳

(安徽财经大学金融学院，安徽蚌埠233030)

0 引言

随着对企业信用评级研究的深入，企业信用评级模型从单变量模型扩展为到Logit和Probit等多变量模型，参数估计方法也从OLS变量估计方法到GMM等方法，企业信用评级模型研究获得了长足的发展.虽然现有主流参数估计方法逐步摆脱同方差和正态分布假定，但在面对非线性分类问题时，上述方法的效果不尽人意.另一方面，人工智能领域新型算法的突破性进展，包括遗传算法和人工神经网络技术等一系列算法的不断成熟，使非线性分类问题解法更为高效可靠，并在多个领域得到了广泛应用.其中，支持向量机(Support Vector Machine，SVM)方法在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中.

由于研究中采用的数据为大规模数据集，而在实际评级活动中通常无法获得大规模样本，因此为了测试样本在小样本环境下的使用效果，我们采用逐级调整样本量的方法探寻模型最适样本量，以保证在提高准确率的前提下减小准确率的波动幅度，从而提高模型的适用性.

1 文献综述

目前已有很多学者对支持向量机方法在信用评级中的应用进行了深入的研究.肖文兵等(2007)运用基于支持向量机方法构建了一个新的个人信用评估预测模型，以期取得更好的预测分类能力.并对SVM分类结果与三层全连接BP神经网络的分类结果进行了比较.结果表明，在判别潜在的贷款申请者中支持向量的判别结果比神经网络的要好.为了减小训练集偏差及为了验证两种方法的鲁棒性，基于两种策略(平衡样本与非平衡样本)交叉验证来进一步评价SVM分类准确性，并对两种方法基于两种策略的误分类作了风险代价分析，发现无论是从分类率还是风险代价角度，支持向量机方法都是一种较好的信用评级方法[1].张目(2010)构建了基于多目标规划的SVM模型，选取沪、深股市2005—2007年的104家企业数据，其中非ST和ST企业各占52家分别定义为正常企业和违约企业两类样本数量相等，符合SVM的学习要求.将实验样本集划分为训练样本集和测试样本集.为了更好的体现SVM对于小样本数据的学习能力以及模型的泛化能力，在保持两类样本数目相当的前提下随机抽取31%(32家)作为训练样本，用于构造SVM模型，剩余的69%(72家)作为测试样本，用于检验模型的泛化能力.通过实证研究发现基于SVM的的企业信用评级具有预测精度高，鲁棒性较好的特征，能够很好的满足企业信用评级的需要[2].沈沛龙等(2010)利用内嵌线性分类方法支持向量机的马克威分析系统为平台构建了中小企业违约概率估计模型，通过对200家中小企业财务数据进行学习、训练进而获得预测模型，找出影响其违约的主要财务因素，并选取训练集以外的250家样本数据进行检验，在构建模型的同时引入相对违约距离的概念，并以此来构造新的违约概率估计模型，并考察了该模型与以往模型的拟合情况，获得了令人满意的结果，通过研究发现这一基于非结构模型给出的违约距离，在信用评级实践中具有重要的应用价值[3].在使用支持向量机模型进行信用评估时，其奇异点和噪声有可能对模型造成影响，为了减小这种干扰的影响，提高模型的判别能力，姚潇，余乐安(2012)在近似支持向量机的基础上，引入模糊思想，提出模糊近似支持向量机模型.为了验证这种模型的有效性，他们分别采用逻辑回归、线性回归、BP神经网络、标准SVM模型、近似SVM模型、模糊近似SVM模型，利用两个公开的信用数据进行实证对比，结果模糊近似SVM模型的总体误判率最低，具有较好的泛化能力[4].

从已有的文献研究可以看出，在企业信用评级中，支持向量机方法与其它方法相比，具有明显的优势.因此，本文采用支持向量机方法探索小企业信用评级的最适样本量.

2 实证研究

2.1 样本数据的选取和处理

根据课题中构建的中小企业信用评级指标体系，首先从《中国工业企业数据库》中提取了安徽省2007年和2008年的相关原始样本数据5 802条，经过筛选剔除不合格的样本，最终选取了安徽省2 980家小企业来探索信用评级最适样本量.

课题研究是将信用的等级个数化为分类问题，因此需要选择合理的分类标准.由于从《中国工业企业数据库》中无法获得企业具体每年从银行获得的贷款额，因此，我们用企业每年的负债总额减去应付账款反映企业每年的贷款额(此贷款额不一定全部是从银行获得)，用连续两年贷款额的差反映企业每年从外部获得的贷款额，我们称之为“负债变动额”.负债变动额的大小反映了企业的不同融资能力.假设负债变动额大于零说明企业这一年从外部获得了贷款，负债变动额小于零说明企业对外部提供了贷款.因此，本研究企业信用等级的划分问题转换为了不同融资能力企业类型的多模式识别问题.分类标准采用负债变动率.

由于中小企业信用评级指标体系中各指标采用的数据单位不一致，同时为了获得较好的分布特征，提高模型的收敛速度，在进行模型训练之前需要对原始数据进行归一化处理，本文采用[0，1]归一化，即将指标体系数据缩放到0至1之间.

2.2 基于支持向量机的信用评级模型的构建

2.2.1 模型参数设置

首先将信用评级的等级个数转换化为分类问题，利用支持向量机处理多维非线性分类的优势对样本企业的信用评级指标数据进行分类.在Matlab(R12)软件中使用LIBSVM工具箱进行模型设计和运算，通过精度比较，我们选用的支持向量机类型为C-SVC(Cr-support Vector Classification)，内积核函数选用径向基函数(Radial Basis Function，RBF)，即

对于二分类情况，设两类企业(获得新增贷款和未获新增贷款)信用评级问题的训练样本为

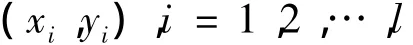
其中，xi∈Rn表示第i个企业的n维评级特征指标的样本数据向量，yi∈{0，1}表示第i个企业的类别，其中“0”表示未获新增贷款，“1”表示当年获得新增贷款.在多分类情况下，在此基础上企业分类根据新增贷款增加率进一步细化.

此时，对企业信用评级问题即转化为寻找最优分类函数

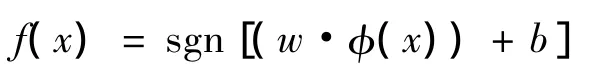
通过对一个二次凸规划问题求解

得到判别函数为

其中K(xi，xj)为核函数，C为一个常数，不同的核函数和C构成了不同的信用评级模型.

支持向量机核函数选取直接决定了模型分类效果的优劣.研究用模型参数的选取采用网格搜索方法，通过逐渐扩大参数值精确探查模型最优参数.

2.2.2 变动样本数量训练模型

为了检验测试样本中负债变动率的极端值对模型精度的影响，我们首先采用固定样本数量，分为删除负债变动率和未删除负债变动率两种情况进行测试.测试结果表明，支持向量机方法对极端值不敏感，具有很好的鲁棒性.

在保证模型测试精度的前提下，为了不增加模型的复杂度，尽可能减少模型训练运算时间的同时，防止模型出现欠学习或过拟合现象的发生，我们进对样本数量进行调整.通过采用步进扩大模型训练样本量的方法，依据训练精度和样本外测试精度，探查一个既能达到一定精度又具有一定运算效率的最优模型训练样本量.

我们首先把安徽省小企业分为小型轻工业1 000家和小型重工业1 980家.在二分类中，小型轻工业采用步进10个样本的方法，即每次模型训练时递增10个样本;对小型重工业我们采用步进50个样本的方法.训练结果如图1、图2所示.

图1 小型重工业精度

由图1可以看出，在样本量比较少的情况下，小型重工业样本内精度和测试精度都有小幅的变化，随着样本量的增加，两者精度都几乎保持不变，从图1得出小型重工业的最适样本量大概在340左右;由图2看出，在样本量比较少的情况下小型轻工业样本内精度和测试精度变化幅度比较大，随着样本量的增加，两者的精度变化的幅度非常小，因此，可以得出小型轻工业的最适样本量大概在130左右.

图2 小型轻工业精度

[1] 肖文兵，费奇，万虎.基于支持向量机的信用评估模型及风险评价[J].华中科技大学学报:自然科学版，2007，35(5):23-26.

[2] 张目.高技术企业信用风险影响因素及评价方法研究[D].成都:电子科技大学，2010.

[3] 沈沛龙，周浩.基于支持向量机理论的中小企业信用风险预测研究[J].国际金融研究，2010(8):77-85.

[4] 姚潇，余乐安.模糊近似支持向量机模型及其在信用风险评估中的应用[J].系统工程理论与实践，2012，32(3):449-554.