区域中小型民营制造业物流管理最优决策模型研究

王棚，谢双双，王蕾，侯艳青

(1.临沂大学理学院，山东临沂276000;2.临沂大学费县分校，山东费县293400)

0 引言

随着我国民营经济的不断发展，中小型民营制造业已经成为我国经济布局中不可缺少的一部分.中小型民营制造业虽然在人员、资产和经营规模上都比同行业小(例如生产产品A的民营企业与国有企业相比)，但是它们却是经济发展重要的组成部分，在经济发展中有着不可替代的作用.随着改革开放与中国经济不断的发展，我国中小型民营制造业也得到了快速、健康和可持续的发展.相应的，中小型民营制造业对地方经济、就业以及创新有着越来越大的作用，已成为推动城市发展的重要力量之一.具体体现在中小企的数量、所创造的价值、提供的就业机会以及创新上[1].

然而，在市场竞争越来越激烈的现代经济环境下，中小型民营制造业面临的挑战也在不断增加.与大型企业相比，中小型民营制造业除了在人员、资产和经营规模上的不足之外，它们往往注重的是“第一利润源”(较少资源消耗)和“第二利润源”(提高劳动生产率)，而大部分忽视了“第三利润源”(加强物流管理)，从而大大削弱了企业的竞争力.当前，中小企业在物流管理方面存在着管理理念落后、管理方式落后、专门人才缺乏、设施利用不足以及物流成本高昂等一系列问题.因此，中小型民营制造业之间的竞争越来越多的体现在生产、经营、运作等物流管理方面.物流管理是中小型民营制造业发展的关键，而建立有效的管理组织，实行严格的物流成本控制是解决竞争困境，提高企业竞争力的有力措施.

随着制造业的发展和需求市场的不断扩大，物流管理均衡模型的研究已经成为一个重要的研究领域，其主要的研究工具是变分不等式和均衡理论.在物流管理研究中，一般包含原材料供应商、制造商、零售商和消费市场，他们之间通过竞争与合作来获得各自的利益.研究的基本目的是在四者中寻找均衡状态，使得原材料供应商、制造商、零售商和消费者的利润达到最大化.在此之前，对于物流管理均衡模型的研究已经不胜枚举.Nagurney A[2]等在2002年提出了第一个物流管理(供应链)的超网络经济模型，该模型将生产网络、销售网络，及运输网络的不同要素综合一体，但是模型中没有考虑原材料供应商和决策主体的交易方式.Chiang W K[3]等人建立了双层双渠道的库存模型，但是没有考虑补贴机制.雷延军[4]等人虽然研究了双渠道三层拓扑模型，但是没有考虑原材料供应商和补贴机制.高自友[5]虽然研究了空间价格均衡中的多商品流模型，可他的研究仅限于制造商和零售商之间的二层供应体系.徐兵[6]等人建立了物流管理各层均衡及整体均衡的条件、经济解释和变分不等式模型，但没有考虑到库存因素.

本文在以上研究的基础上，针对中小型民营制造业的物流管理均衡模型进行研究，考虑补贴机制、库存成本以及包含传统销售和网络销售的双重渠道，建立了中小型民营制造业的物流管理最优决策模型，给出了经济解释，从而得出了制造商最优化决策策略.

1 中小型民营制造商行为分析与模型建立

1.1 模型假设

分别考虑m个原材料供应商、n个中小民营制造商、h个零售商和g个消费市场，针对中小民营制造商在物流管理均衡决策，作出如下假设:物流管理中的同层制造商为非合作竞争且生产同质无差异产品;所有制造商的决策行为都是理性的，即制造商追求利润最大化，风险最小化;不考虑供小于求的情况，即每个决策单位必定满足需求;市场需求和产品价格都是内生变量;制造商的成本包括原材料成本、生产成本、运输成本(包括搬运、交通等费用)、补贴成本和库存成本;单个原材料供应商只提供一种原材料;制造商生产产品所需的原材料种类共需t种;每一原材料的采购只从单个原材料供应商处获取(则采购t种原材料需要t个原材料供应商);所有成本函数均为连续且凸的;制造商与零售商之间制定了补贴机制，即如果零售商有该产品的库存，则制造商需要向零售商按库存量补贴一定量的金钱.

1.2 制造商与原材料供应商之间的行为分析

为了论述方便，假设有第k个材料供应商、第i个制造商、第d个零售商、第j个消费市场.

对于制造商来说，与原材料供应商之间的行为只会产生成本，而不会产生收益，所以制造商和原材料供应商之间的行为分析如下.r表示原材料供应商，r∈R，原材料供应商集合R={1，2，…，r，…，m};pr表示原材料供应商r的原材料单价;i表示制造商，i∈I，制造商集合I={1，2，…，i，…，n};k表示在对原材料性价比分析的基础上所选择的原材料供应商，k∈K，被选原材料供应商集合K={1，2，…，k，…，t}，制造商对原材料供应商的选择主要是通过各个原材料供应商所提供原材料的性价比的比较来确定，其中，性价比=原材料质量/原材料价格表示制造商i通过销售渠道a对原材料k的购买单价(a=1表示传统销售渠道，a=2表示网络销售渠道，下面符号含义相同);表示制造商i通过销售渠道a对原材料k的购买量;表示第i个制造商从第k个原材料供应商购买原材料的运输成本，记为=根据总成本=购买原材料成本+运输成本，则第i个制造商购买原材料k的总成本为

式(1)中第1个算式表示制造商i购买原材料的成本，第2个算式表示制造商i购买原材料的运输成本.

从以上制造商和原材料供应商的分析可以得出如下结论:对于制造商来说，购买原材料只会产生成本(不考虑原材料可用于生产的价值)，所以制造商只有降低与原材料供应商交易所产生的基于式(1)的成本，才能间接地使自己的利益达到最大.

1.3 制造商与零售商和消费市场之间的行为分析

为了论述方便，令d表示零售商，d∈D，零售商集合D={1，2，…，d，…，h};j表示消费市场，j∈J，消费市场集合J={1，2，…，j，…，g};表示零售商d通过渠道a购买制造商i生产的产品单价;表示零售商d通过渠道a从制造商i所购买的产品量表示消费市场j通过渠道a从制造商i所购买的产品单价表示消费市场j通过渠道a从制造商i所购买的产品量;qi表示制造商i的产品销售总量，可得

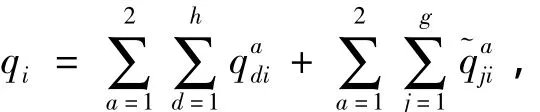
Q2表示所有制造商与消费市场的交易总量，可得

Ni表示制造商i的库存成本，记为Ni=Ni(－qi)，Mj表示所有零售商的库存(这里的库存只与制造商i的产品有关)，假如引入制造商对零售商的库存补贴机制，令Nj为制造商对零售商库存的补贴成本，记为Nj=Nj(Mj)，fi表示制造商i的生产成本函数，是其产品生产数量的严格连续可微的凸函数，fi=fi().

由前面的假设知，制造商i服从理性经济人假设，即追求利益最大化，风险最小化.假设制造商i的风险函数ri是连续的凸函数，由自身的产品出货量和其他竞争者的产品出货来决定，即ri=ri(Q1，Q2)，对于任意的i，制造商i的风险最小化条件为:

其中qdi表示制造商i销售给零售商d的产品总量表示制造商i销售给消费市场j的产品总量.

假设制造商i的风险最小化目标的权系数为αi;利润最大化目标的权系数为1，这里用一个连续的带有权系数的价值函数表示制造商i对于零售商和消费市场的优化决策问题:

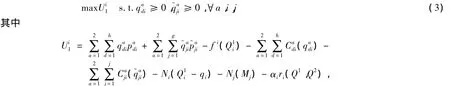
从制造商与零售商及消费市场行为分析可以得出如下结论:制造商与零售商及销售市场之间不仅产生收益，还产生成本，若要制造商利益最大化，则制造商除了需要尽量销售更多产品，还需要根据需求市场的需求量来生产产品，否则，生产的产品过多，会使库存成本及补贴成本增加，导致收益降低.

1.4 制造商最优化决策模型建立

为了追求制造商的利益最大化，需要将(2)得出的制造商和原材料供应商之间的行为关系式(1)和(3)得出的制造商与零售商和消费市场之间的行为关系式(3)整合在一起，可以得出制造商分别与原材料供应商、零售商和消费市场之间的最优化决策行为公式:

制造商是在非合作环境下竞争，因此每一个制造商i都在追求利益最大化和风险最小化，在以上的假设条件下，利用约束最优化的相关理论，式(4)可等价的转化为下面的问题，即求一向量

从经济学的角度分析，式(5)中第1个式子表明，无论制造商i与零售商j以何种方式进行交易，只要其产品交易量大于零，那么产品的边际生产成本、边际交易成本、边际库存成本、边际补贴成本以及边际风险五者之和等于与零售商的产品交易价格.反之，产品的交易量就等于零.第2个式子表明，如果制造商的边际生产成本、边际交易成本以及边际风险三者之和等于与消费者的产品交易价格，那么制造商与消费者之间的交易量就一定大于零，反之，产品交易就等于零.同理，第3个式子表明如果制造商的边际运输成本等于与原材料供应商的材料价格，那么制造商与原材料供应商之间的交易量一定大于零，反之，原材料交易量等于零.

通过分别分析制造商与原材料供应商、零售商和消费市场之间的行为，得出对于制造商来说，原材料购买量、原材料价格、产品价格、产品流量、库存量和补贴机制满足式(5).显然(5)等价于下面的形式:求一向量x∈Ran(h+g+t)+，使得

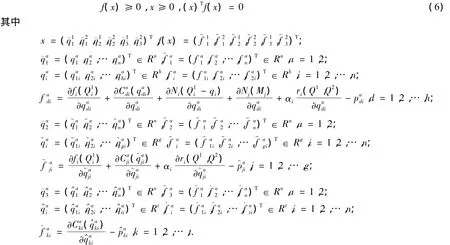
因此，我们有下面的结论成立.

结论1制造商最优决策模型式(6)的解当且仅当是制造商的一个最优化决策.

2 算例

构造一个由2个原材料供应商、2个制造商、2个零售商、2个消费市场、存在网络销售和传统销售及补贴机制组成的最优化决策模型.即t=2，n=2，h=2，g=2，a=2.制造商和原材料供应商的运输成本函数如下:

其中，a=1，2;i=1，2;k=1，2;制造商的生产成本函数如下式所示:

制造商的库存成本函数如下所示:

其中i=1，2;制造商的补贴机制函数:Nj(Mj)=4Mj，其中，j=1，2;制造商与零售商的运输成本函数如下所示:

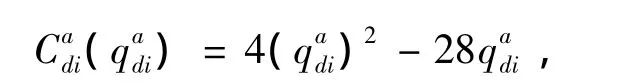
其中d=1，2;i=1，2;a=1，2;不妨设制造商的风险函数

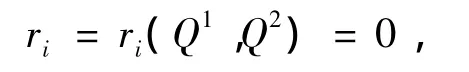
制造商与消费市场的运输成本函数如下所示:

其中j=1，2;i=1，2;a=1，2;根据式(1)、(3)～(6)，将以上函数表达式带入其中，得出:

因此，可以得到列向量

因此，我们有f(x)=Mx+p，其中

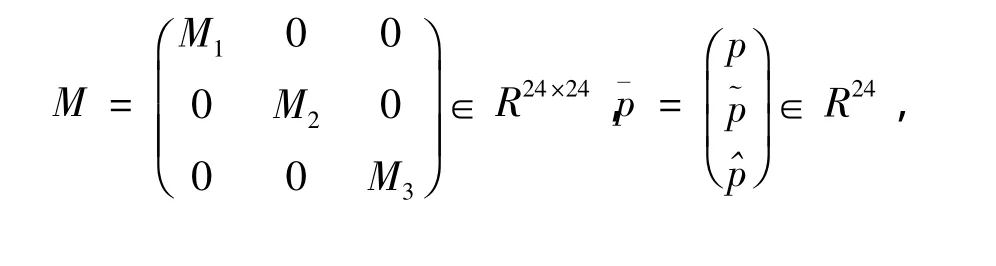
对于问题(6)，利用Xie等提出的算法[7]，可得出问题(6)的解向量

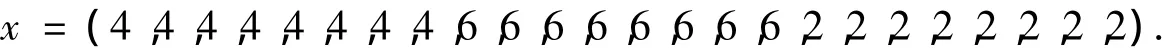
3 结论

本文基于对小型民营制造业物流管理的分析，通过对众多前人的研究和参考，得出了中小型制造商达到利润最大化和风险最小化的最优化决策模型.在该模型里考虑了两种交易行为，即传统交易和网络交易;考虑了商品的竞争风险和存货风险并给出了制造商对零售商的补贴机制.从数学的角度给出了制造商的最优化决策策略.但是，该模型的不足之处是没有考虑到制造商的多商品流的管理及优化和随机市场需求下的物流管理及优化，也没有更加深入地讨论原材料供应商、零售商和消费市场的利益最大化，即没有探讨原材料供应商、制造商、零售商和消费市场他们共同最求利益最大化风险最小化的均衡条件，这是将来探讨的课题.

[1] 李德福.中小企业物流管理优化策略研究[J].物流科技，2010(2):53-55.

[2] Nagurney A，Dong J.Supernetworks:Decision-Making for the Information Age[M].Edward Elgar Publishing，2002.

[3] Chiang W K，Monahan G E.Managing inventories in a two-echelon dual-channel supply chain[J].European Journal of Operational Research，2005，162(2):325-341.

[4] 雷延军，李向阳.基于风险与双渠道的全球供应链“超网络”均衡优化模型研究[J].中国管理科学，2006(14):524-528.

[5] 高自友，孙慧君.现代物流与交通运输系统[M].北京:人民交通出版社，2003.

[6] 徐兵，朱道立.产品随机选择下多商品流供应链网络均衡模型研究[J].系统工程理论与实践，2007(3):83-104.

[7] Xie S S，Wang P.An Algorithm for the Nonlinear Complementarity Problem On Management Equilibrium Model[J].International Journal of Computer and Information Technology，2013，11(2):1136-1140.